Logarithmic Equations

Learning Outcomes

Solve a logarithmic equation algebraically.
Solve a logarithmic equation graphically.
Use the one-to-one property of logarithms to solve a logarithmic equation.
Solve a radioactive decay problem.

We have already seen that every logarithmic equation ${\mathrm{log}}_{b}\left(x\right)=y$ is equal to the exponential equation ${b}^{y}=x$ . We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

For example, consider the equation ${\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3$ . To solve this equation, we can use rules of logarithms to rewrite the left side as a single log and then apply the definition of logs to solve for $x$ :

$\begin{array}{l}{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3\hfill & \hfill \\ \text{ }{\mathrm{log}}_{2}\left(2\left(3x - 5\right)\right)=3\hfill & \text{Apply the product rule of logarithms}.\hfill \\ \text{ }{\mathrm{log}}_{2}\left(6x - 10\right)=3\hfill & \text{Distribute}.\hfill \\ \text{ }{2}^{3}=6x - 10\hfill & \text{Convert to exponential form}.\hfill \\ \text{ }8=6x - 10\hfill & \text{Calculate }{2}^{3}.\hfill \\ \text{ }18=6x\hfill & \text{Add 10 to both sides}.\hfill \\ \text{ }x=3\hfill & \text{Divide both sides by 6}.\hfill \end{array}$

A General Note: Using the Definition of a Logarithm to Solve Logarithmic Equations

For any algebraic expression S and real numbers b and c, where $b>0,\text{ }b\ne 1$ ,

${\mathrm{log}}_{b}\left(S\right)=c\text{ if and only if }{b}^{c}=S$

Example: Using Algebra to Solve a Logarithmic Equation

Solve $2\mathrm{ln}x+3=7$ .

Show Solution

$\begin{array}{l}2\mathrm{ln}x+3=7\hfill & \hfill \\ \text{}2\mathrm{ln}x=4\hfill & \text{Subtract 3 from both sides}.\hfill \\ \text{}\mathrm{ln}x=2\hfill & \text{Divide both sides by 2}.\hfill \\ \text{}x={e}^{2}\hfill & \text{Rewrite in exponential form}.\hfill \end{array}$

Try It

Solve $6+\mathrm{ln}x=10$ .

Show Solution

$x={e}^{4}$

Example: Using Algebra Before and After Using the Definition of the Natural Logarithm

Solve $2\mathrm{ln}\left(6x\right)=7$ .

Show Solution

$\begin{array}{l}2\mathrm{ln}\left(6x\right)=7\hfill & \hfill \\ \text{}\mathrm{ln}\left(6x\right)=\frac{7}{2}\hfill & \text{Divide both sides by 2}.\hfill \\ \text{}6x={e}^{\left(\frac{7}{2}\right)}\hfill & \text{Use the definition of }\mathrm{ln}.\hfill \\ \text{}x=\frac{1}{6}{e}^{\left(\frac{7}{2}\right)}\hfill & \text{Divide both sides by 6}.\hfill \end{array}$

Try It

Solve $2\mathrm{ln}\left(x+1\right)=10$ .

Show Solution

$x={e}^{5}-1$

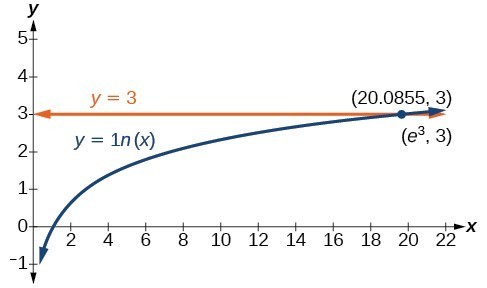
Example: Using a Graph to Understand the Solution to a Logarithmic Equation

Solve $\mathrm{ln}x=3$ .

Show Solution

$\begin{array}{l}\mathrm{ln}x=3\hfill & \hfill \\ x={e}^{3}\hfill & \text{Use the definition of }\mathrm{ln}\text{.}\hfill \end{array}$

Below is a graph of the equation. On the graph the x-coordinate of the point where the two graphs intersect is close to 20. In other words ${e}^{3}\approx 20$ . A calculator gives a better approximation: ${e}^{3}\approx 20.0855$ .

Graph of two questions, y=3 and y=ln(x), which intersect at the point (e^3, 3) which is approximately (20.0855, 3).

The graphs of $y=\mathrm{ln}x$ and y = 3 cross at the point $\left(e^3,3\right)$ which is approximately (20.0855, 3).

Try It

Use a graphing calculator to estimate the approximate solution to the logarithmic equation ${2}^{x}=1000$ to 2 decimal places.

Show Solution

$x\approx 9.97$

Using the One-to-One Property of Logarithms to Solve Logarithmic Equations

As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers x > 0, S > 0, T > 0 and any positive real number b, where $b\ne 1$ ,

${\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T$

For example,

$\text{If }{\mathrm{log}}_{2}\left(x - 1\right)={\mathrm{log}}_{2}\left(8\right),\text{then }x - 1=8$

So if $x - 1=8$ , then we can solve for x and we get x = 9. To check, we can substitute x = 9 into the original equation: ${\mathrm{log}}_{2}\left(9 - 1\right)={\mathrm{log}}_{2}\left(8\right)=3$ . In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.

For example, consider the equation $\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)$ . To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm and then apply the one-to-one property to solve for x:

$\begin{array}{l}\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(\frac{3x - 2}{2}\right)=\mathrm{log}\left(x+4\right)\hfill & \text{Apply the quotient rule of logarithms}.\hfill \\ \text{}\frac{3x - 2}{2}=x+4\hfill & \text{Apply the one-to-one property}.\hfill \\ \text{}3x - 2=2x+8\hfill & \text{Multiply both sides of the equation by }2.\hfill \\ \text{}x=10\hfill & \text{Subtract 2}x\text{ and add 2}.\hfill \end{array}$

To check the result, substitute x = 10 into $\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)$ .

$\begin{array}{l}\mathrm{log}\left(3\left(10\right)-2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(\left(10\right)+4\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(28\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(14\right)\hfill & \hfill \\ \text{}\mathrm{log}\left(\frac{28}{2}\right)=\mathrm{log}\left(14\right)\hfill & \text{The solution checks}.\hfill \end{array}$

A General Note: Using the One-to-One Property of Logarithms to Solve Logarithmic Equations

For any algebraic expressions S and T and any positive real number b, where $b\ne 1$ ,

${\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T$

Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.

How To: Given an equation containing logarithms, solve it using the one-to-one property

Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation is of the form ${\mathrm{log}}_{b}S={\mathrm{log}}_{b}T$ .
Use the one-to-one property to set the arguments equal to each other.
Solve the resulting equation, S = T, for the unknown.

Example: Solving an Equation Using the One-to-One Property of Logarithms

Solve $\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)$ .

Show Solution

$\begin{array}{l}\text{ }\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)\hfill & \hfill \\ \text{ }{x}^{2}=2x+3\hfill & \text{Use the one-to-one property of the logarithm}.\hfill \\ \text{ }{x}^{2}-2x - 3=0\hfill & \text{Get zero on one side before factoring}.\hfill \\ \left(x - 3\right)\left(x+1\right)=0\hfill & \text{Factor using FOIL}.\hfill \\ \text{ }x - 3=0\text{ or }x+1=0\hfill & \text{If a product is zero, one of the factors must be zero}.\hfill \\ \text{ }x=3\text{ or }x=-1\hfill & \text{Solve for }x.\hfill \end{array}$

Analysis of the Solution

There are two solutions: x = 3 or x = –1. The solution x = –1 is negative, but it checks when substituted into the original equation because the argument of the logarithm function is still positive.

Try It

Solve $\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}1$ .

Show Solution

$x=1$ or $x=–1$

Module 4: Inverse, Exponential, and Logarithmic Functions