Define and solve an equation that represents the concentration of a mixture
Propotions
Matryoshka, or nesting dolls.
A proportion is a statement that two ratios are equal to each other. There are many things that can be represented with ratios, including the actual distance on the earth that is represented on a map. In fact, you probably use proportional reasoning on a regular basis and don’t realize it. For example, say you have volunteered to provide drinks for a community event. You are asked to bring enough drinks for 35-40 people. At the store you see that drinks come in packages of 12. You multiply 12 by 3 and get 36 – this may not be enough if 40 people show up, so you decide to buy 4 packages of drinks just to be sure.
This process can also be expressed as a proportional equation and solved using mathematical principles. First, we can express the number of drinks in a package as a ratio:
Then we express the number of people who we are buying drinks for as a ratio with the unknown number of packages we need. We will use the maximum so we have enough.
[latex]\frac{40\text{ people }}{x\text{ packages }}[/latex]
We can find out how many packages to purchase by setting the expressions equal to each other:
[latex]\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}[/latex]
To solve for x, we can use techniques for solving linear equations, or we can cross multiply as a shortcut.
[latex]\begin{array}{l}\,\,\,\,\,\,\,\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\\\text{}\\x\cdot\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\cdot{x}\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,12x=40\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=\frac{40}{12}=\frac{10}{3}=3.33\end{array}[/latex]
We can round up to 4 since it doesn’t make sense to by 0.33 of a package of drinks. Of course, you don’t write out your thinking this way when you are in the grocery store, but doing so helps you to be able to apply the concepts to less obvious problems. In the following example we will show how to use a proportion to find the number of people on the planet who don’t have access to a toilet. Because, why not?
Example
As of March, 2016 the world’s population was estimated at 7.4 billion. [1]. According to water.org, 1 out of every 3 people on the planet lives without access to a toilet. Find the number of people on the planet that do not have access to a toilet.
Show Solution
We can use a proportion to find the unknown number of people who live without a toilet since we are given that 1 in 3 don’t have access, and we are given the population of the planet.
We know that 1 out of every 3 people don’t have access, so we can write that as a ratio (fraction)
[latex]\frac{1}{3}[/latex].
Let the number of people without access to a toilet be x. The ratio of people with and without toilets is then
[latex]\frac{x}{7.4\text{ billion }}[/latex]
Equate the two ratios since they are representing the same fractional amount of the population.
The original units were billions of people, so our answer is [latex]2.46[/latex] billion people don’t have access to a toilet. Wow, that’s a lot of people.
Answer
2.46 billion people don’t have access to a toilet.
In the next example, we will use the length of a person’t femur to estimate their height. This process is used in forensic science and anthropology, and has been found in many scientific studies to be a very good estimate.
Example
It has been shown that a person’s height is proportional to the length of their femur [2]. Given that a person who is 71 inches tall has a femur length of 17.75 inches, how tall is someone with a femur length of 16 inches?
Show Solution
Height and femur length are proportional for everyone, so we can define a ratio with the given height and femur length. We can then use this to write a proportion to find the unknown height.
Let x be the unknown height. Define the ratio of femur length and height for both people using the given measurements.
Person 1: [latex]\frac{\text{femur length}}{\text{height}}=\frac{17.75\text{inches}}{71\text{inches}}[/latex]
Person 2: [latex]\frac{\text{femur length}}{\text{height}}=\frac{16\text{inches}}{x\text{inches}}[/latex]
Equate the ratios, since we are assuming height and femur length are proportional for everyone.
The unknown height of person 2 is 64 inches. In general, we can reduce the fraction [latex]\frac{17.75}{71}=0.25=\frac{1}{4}[/latex] to find a general rule for everyone. This would translate to sayinga person’s height is 4 times the length of their femur.
Another way to describe the ratio of femur length to height that we found in the last example is to say there’s a 1:4 ratio between femur length and height, or 1 to 4.
Ratios are also used in scale drawings. Scale drawings are enlarged or reduced drawings of objects, buildings, roads, and maps. Maps are smaller than what they represent and a drawing of dendritic cells in your brain is most likely larger than what it represents. The scale of the drawing is a ratio that represents a comparison of the length of the actual object and it’s representation in the drawing. The image below shows a map of the us with a scale of 1 inch representing 557 miles. We could write the scale factor as a fraction [latex]\frac{1}{557}[/latex] or as we did with the femur-height relationship, 1:557.
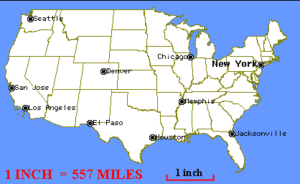
Map with scale factor
In the next example we will use the scale factor given in the image above to find the distance between Seattle Washington and San Jose California.
Example
Given a scale factor of 1:557 on a map of the US, if the distance from Seattle, WA to San Jose, CA is 1.5 inches on the map, define a proportion to find the actual distance between them.
Show Solution
We need to define a proportion to solve for the unknown distance between Seattle and San Jose.
The scale factor is 1:557, and we will call the unknown distance x. The ratio of inches to miles is [latex]\frac{1}{557}[/latex].
We know inches between the two cities, but we don’t know miles, so the ratio that describes the distance between them is [latex]\frac{1.5}{x}[/latex].
The proportion that will help us solve this problem is [latex]\frac{1}{557}=\frac{1.5}{x}[/latex].
Solve using the common denominator [latex]557x[/latex] to clear fractions.
We used the scale factor 1:557 to find an unknown distance between Seattle and San Jose. We also checked our answer of 835.5 miles with Google maps, and found that the distance is 839.9 miles, so we did pretty well!
In the next example, we will find a scale factor given the length between two cities on a map, and their actual distance from each other.
Example
Two cities are 2.5 inches apart on a map. Their actual distance from each other is 325 miles. Write a proportion to represent and solve for the scale factor for one inch of the map.
Show Solution
We know that for each 2.5 inches on the map, it represents 325 actual miles. We are looking for the scale factor for one inch of the map.
The ratio we want is [latex]\frac{1}{x}[/latex] where x is the actual distance represented by one inch on the map. We know that for every 2.5 inches, there are 325 actual miles, so we can define that relationship as [latex]\frac{2.5}{325}[/latex]
We can use a proportion to equate the two ratios and solve for the unknown distance.
The scale factor for one inch on the map is 1:130, or for every inch of map there are 130 actual miles.
In the video that follows, we present an example of using proportions to obtain the correct amount of medication for a patient, as well as finding a desired mixture of coffees.
Rational formulas
Rational formulas can be useful tools for representing real-life situations and for finding answers to real problems. Equations representing direct, inverse, and joint variation are examples of rational formulas that can model many real-life situations. As you will see, if you can find a formula, you can usually make sense of a situation.
When solving problems using rational formulas, it is often helpful to first solve the formula for the specified variable. For example, work problems ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, [latex]W=rt[/latex]. The amount of work done (W) is the product of the rate of work (r) and the time spent working (t). Using algebra, you can write the work formula 3 ways:
[latex]W=rt[/latex]
Find the time (t):[latex] t=\frac{W}{r}[/latex] (divide both sides by r)
Find the rate (r):[latex] r=\frac{W}{t}[/latex](divide both sides by t)
Example
The formula for finding the density of an object is [latex] D=\frac{m}{v}[/latex], where D is the density, m is the mass of the object and v is the volume of the object. Rearrange the formula to solve for the mass (m) and then for the volume (v).
Show Solution
Start with the formula for density.
[latex] D=\frac{m}{v}[/latex]
Multiply both side of the equation by v to isolate m.
[latex] m=D\cdot v[/latex] and [latex] v=\frac{m}{D}[/latex]
Now let’s look at an example using the formula for the volume of a cylinder.
Example
The formula for finding the volume of a cylinder is [latex]V=\pi{r^{2}}h[/latex], where V is the volume, r is the radius and h is the height of the cylinder. Rearrange the formula to solve for the height (h).
Show Solution
Start with the formula for the volume of a cylinder.
[latex] V=\pi{{r}^{2}}h[/latex]
Divide both sides by [latex] \pi {{r}^{2}}[/latex] to isolate h.
Simplify. You find the height, h, is equal to [latex] \frac{V}{\pi {{r}^{2}}}[/latex].
[latex] \frac{V}{\pi {{r}^{2}}}=h[/latex]
Answer
[latex] h=\frac{V}{\pi {{r}^{2}}}[/latex]
In the following video we give another example of solving for a variable in a formula, or as they are also called, a literal equation.
Work
Rational equations can be used to solve a variety of problems that involve rates, times and work. Using rational expressions and equations can help you answer questions about how to combine workers or machines to complete a job on schedule.
A Good Day’s Work
A “work problem” is an example of a real life situation that can be modeled and solved using a rational equation. Work problems often ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, [latex]W=rt[/latex]. (Notice that the work formula is very similar to the relationship between distance, rate, and time, or [latex]d=rt[/latex].) The amount of work done (W) is the product of the rate of work (r) and the time spent working (t). The work formula has 3 versions.
Some work problems include multiple machines or people working on a project together for the same amount of time but at different rates. In that case, you can add their individual work rates together to get a total work rate. Let’s look at an example.
Example
Myra takes 2 hours to plant 50 flower bulbs. Francis takes 3 hours to plant 45 flower bulbs. Working together, how long should it take them to plant 150 bulbs?
Show Solution
Think about how many bulbs each person can plant in one hour. This is their planting rate.
Myra: [latex] \frac{50\,\,\text{bulbs}}{2\,\,\text{hours}}[/latex], or [latex] \frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}[/latex]
Francis: [latex] \frac{45\,\,\text{bulbs}}{3\,\,\text{hours}}[/latex], or [latex] \frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}[/latex]
Combine their hourly rates to determine the rate they work together.
Use one of the work formulas to write a rational equation, for example [latex] r=\frac{W}{t}[/latex]. You know r, the combined work rate, and you know W, the amount of work that must be done. What you don’t know is how much time it will take to do the required work at the designated rate.
[latex] \frac{40}{1}=\frac{150}{t}[/latex]
Solve the equation by multiplying both sides by the common denominator, then isolating t.
It should take 3 hours 45 minutes for Myra and Francis to plant 150 bulbs together.
Other work problems go the other way. You can calculate how long it will take one person to do a job alone when you know how long it takes people working together to complete the job.
Example
Joe and John are planning to paint a house together. John thinks that if he worked alone, it would take him 3 times as long as it would take Joe to paint the entire house. Working together, they can complete the job in 24 hours. How long would it take each of them, working alone, to complete the job?
Show Solution
Choose variables to represent the unknowns. Since it takes John 3 times as long as Joe to paint the house, his time is represented as 3x.
Let x = time it takes Joe to complete the job
3x = time it takes John to complete the job
The work is painting 1 house or 1. Write an expression to represent each person’s rate using the formula [latex] r=\frac{W}{t}[/latex].
Joe’s rate: [latex] \frac{1}{x}[/latex]
John’s rate: [latex] \frac{1}{3x}[/latex]
Their combined rate is the sum of their individual rates. Use this rate to write a new equation using the formula [latex]W=rt[/latex].
The problem states that it takes them 24 hours together to paint a house, so if you multiply their combined hourly rate [latex] \left( \frac{1}{x}+\frac{1}{3x} \right)[/latex] by 24, you will get 1, which is the number of houses they can paint in 24 hours.
The solution checks. Since [latex]x=32[/latex], it takes Joe 32 hours to paint the house by himself. John’s time is 3x, so it would take him 96 hours to do the same amount of work.
Answer
It takes 32 hours for Joe to paint the house by himself and 96 hours for John the paint the house himself.
In the video that follows, we show another example of finding one person’s work rate given a combined work rate.
As shown above, many work problems can be represented by the equation [latex] \frac{t}{a}+\frac{t}{b}=1[/latex], where t is the time to do the job together, a is the time it takes person A to do the job, and b is the time it takes person B to do the job. The 1 refers to the total work done—in this case, the work was to paint 1 house.
The key idea here is to figure out each worker’s individual rate of work. Then, once those rates are identified, add them together, multiply by the time t, set it equal to the amount of work done, and solve the rational equation.
We present another example of two people painting at different rates in the following video.
Motion
We have solved uniform motion problems using the formula [latex]D = rt[/latex] in previous chapters. We used a table like the one below to organize the information and lead us to the equation.
The formula [latex]D=rt[/latex] assumes we know [latex]r[/latex] and [latex]t[/latex] and use them to find [latex]D[/latex]. If we know [latex]D[/latex] and [latex]r[/latex] and need to find [latex]t[/latex], we would solve the equation for [latex]t[/latex] and get the formula [latex]\displaystyle t=\frac{D}{r}[/latex].
ExAMPLE
Greg went to a conference in a city 120 miles away. On the way back, due to road construction he had to drive 10 mph slower which resulted in the return trip taking 2 hours longer. How fast did he drive on the way to the conference?
A man rows down stream for 30 miles then turns around and returns to his original location, the total trip took 8 hours. If the current flows at 2 miles per hour, how fast would the man row in still water?
Mixtures are made of ratios of different substances that may include chemicals, foods, water, or gases. There are many different situations where mixtures may occur both in nature and as a means to produce a desired product or outcome. For example, chemical spills, manufacturing and even biochemical reactions involve mixtures. The thing that can make mixtures interesting mathematically is when components of the mixture are added at different rates and concentrations. In our last example we will define an equation that models the concentration – or ratio of sugar to water – in a large mixing tank over time. You are asked whether the final concentration of sugar is greater than the concentration at the beginning.
Example
A large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed. A tap will open pouring 10 gallons per minute of water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the concentration (pounds per gallon) of sugar in the tank after 12 minutes. Is that a greater concentration than at the beginning?
Show Answer
Let t be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is a linear equation, as is the amount of sugar in the tank. We can write an equation independently for each:
[latex]\begin{cases}\text{water: }W\left(t\right)=100+10t\text{ in gallons}\\ \text{sugar: }S\left(t\right)=5+1t\text{ in pounds}\end{cases}\\[/latex]
The concentration, C, will be the ratio of pounds of sugar to gallons of water
Obialor, Ambrose, Churchill Ihentuge, and Frank Akapuaka. "Determination of Height Using Femur Length in Adult Population of Oguta Local Government Area of Imo State Nigeria." Federation of American Societies for Experimental Biology, April 2015. Accessed June 22, 2016. http://www.fasebj.org/content/29/1_Supplement/LB19.short. ↵
Licenses and Attributions
CC licensed content, Original
Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
Ex: Direct Variation Application - Aluminum Can Usage. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/DLPKiMD_ZZw. License: CC BY: Attribution
Joint Variation: Determine the Variation Constant (Volume of a Cone). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/JREPATMScbM. License: CC BY: Attribution
Ex 1: Rational Equation Application - Painting Together. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/SzSasnDF7Ms. License: CC BY: Attribution
Rational Function Application - Concentration of a Mixture. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/GD6H7BE_0EI. License: CC BY: Attribution
CC licensed content, Shared previously
Unit 15: Rational Expressions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. License: CC BY: Attribution
