Learning Outcomes
- Identify solutions of systems of equations
- Solve systems of equations by graphing
A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a unique solution.
In this section, we will look at systems of linear equations in two variables which consist of two equations that each contain two different variables. For example, consider the following system of linear equations in two variables.
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair [latex](4, 7)[/latex] is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly, we will investigate methods of finding such a solution if it exists.
In addition to considering the number of equations and variables, we can categorize systems of linear equations by the number of solutions. A consistent system of equations has at least one solution. A consistent system is considered to be an independent system if it has a single solution like the example we just explored. The two lines have different slopes and intersect at one point in the plane. A consistent system is considered to be a dependent system if the equations have the same slope and the same y-intercepts. In other words, the lines coincide, so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions.
Another type of system of linear equations is an inconsistent system which is one where the equations represent two parallel lines. The lines have the same slope and different y-intercepts. There are no points common to both lines; hence, there is no solution to the system.
A General Note: Types of Linear Systems
There are three types of systems of linear equations in two variables and three types of solutions.
- An independent system has exactly one solution pair [latex]\left(x,y\right)[/latex]. The point where the two lines intersect is the only solution.
- An inconsistent system has no solution.The two lines are parallel and will never intersect.
- A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.
Below are graphical representations of each type of system.
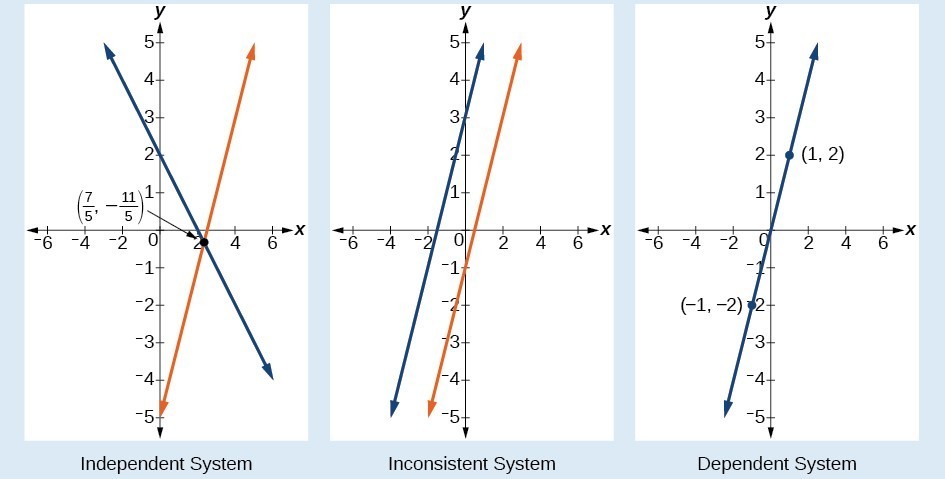
The independent and dependent systems are also consistent because they both have at least one solution.
How To: Given a system of linear equations and an ordered pair, determine whether the ordered pair is a solution
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.
Example
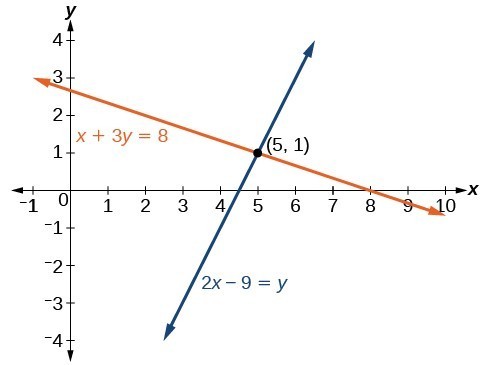
Determine whether the ordered pair [latex]\left(5,1\right)[/latex] is a solution to the given system of equations.
In the following video, we will show another example of how to verify whether an ordered pair is a solution to a system of equations.
Solving Systems of Equations by Graphing
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.
Example
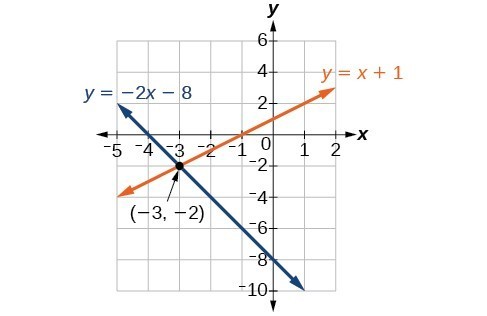
Solve the following system of equations by graphing. Identify the type of system.
[latex]\begin{array}{c}2x+y=-8\\ x-y=-1\end{array}[/latex]
Graphing can be used if the system is inconsistent or dependent. In both cases, we can still graph the system to determine the type of system and solution. If the two lines are parallel, the system has no solution and is inconsistent. If the two lines are identical, the system has infinite solutions and is a dependent system.
In the following video, we show another example of how to identify whether a graphed system has a solution and identify what type of solution is represented.
In our last video, we show how to solve a system of equations by first graphing the lines and then identifying the solution the system has.
Solve Systems by Substitution
Learning Outcomes
- Solve systems of equations by substitution
- Identify inconsistent systems of equations containing two variables
Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. We will consider two more methods of solving a system of linear equations that are more precise than graphing. One such method is solving a system of equations by the substitution method where we solve one of the equations for one variable and then substitute the result into the other equation to solve for the second variable. Recall that we can solve for only one variable at a time which is the reason the substitution method is both valuable and practical.
How To: Given a system of two equations in two variables, solve using the substitution method
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, and then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the other variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
Example
Solve the following system of equations by substitution.
In the following video, you will be given an example of solving a system of two equations using the substitution method.
If you had chosen the other equation to start with in the previous example, you would still be able to find the same solution. It is really a matter of preference, because sometimes solving for a variable will result in having to work with fractions. As you become more experienced with algebra, you will be able to anticipate what choices will lead to more desirable outcomes.
Recall that an inconsistent system consists of parallel lines that have the same slope but different y-intercepts. They will never intersect. When searching for a solution to an inconsistent system, we will come up with a false statement such as [latex]12=0[/latex].
Example
Solve the following system of equations.
[latex]\begin{array}{l}x=9 - 2y\hfill \\ x+2y=13\hfill \end{array}[/latex]
In the next video, we show another example of using substitution to solve a system that has no solution.
In our next video, we show that a system can have an infinite number of solutions.
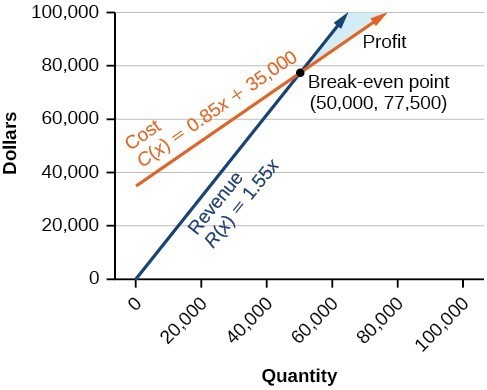
Consider a skateboard manufacturer’s revenue function; this is the function used to calculate the amount of money that comes into the business. It can be represented by the equation [latex]R=xp[/latex], where [latex]x=[/latex] quantity and [latex]p=[/latex] price. The revenue function is shown in orange in the graph below.
The cost function is the function used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs, such as utilities. The cost function is shown in blue in the graph below. The x-axis represents the quantity of skateboards produced and sold in hundreds of units. The y-axis represents either cost or revenue in hundreds of dollars.
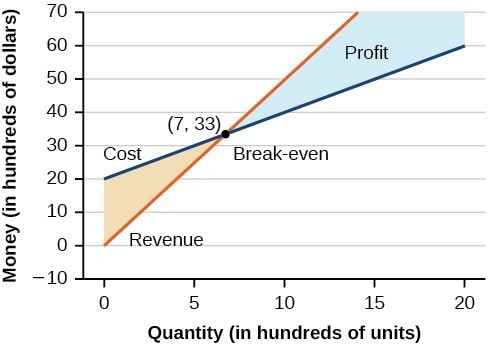
The point at which the two lines intersect is called the break-even point. We can see from the graph that if 700 units are produced, the cost is [latex]$3,300[/latex] and the revenue is also [latex]$3,300[/latex]. In other words, the company breaks even if they produce and sell 700 units. They neither make money nor lose money.
The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss.
Example
Given the cost function [latex]C\left(x\right)=0.85x+35,000[/latex] and the revenue function [latex]R\left(x\right)=1.55x[/latex], find the break-even point.
In the next example, we will show how to write a system of linear equations given attendance and ticket cost data. We will then find the number of tickets purchased based on our system.
Example
The cost of a ticket to the circus is [latex]$25.00[/latex] for children and [latex]$50.00[/latex] for adults. On a certain day, attendance at the circus is [latex]2,000[/latex] and the total gate revenue is [latex]$70,000[/latex]. How many children and how many adults bought tickets?
In our last video example, we show how to set up a system of linear equations that represents the total cost for admission to a museum.
In the next section, we will introduce more methods for solving systems of equations that cannot be easily solved by substitution.