Solutions

Solutions to Try Its

1. [latex]\left(2,\infty \right)\\[/latex]

2. [latex]\left(5,\infty \right)\\[/latex]

3. The domain is [latex]\left(0,\infty \right)\\[/latex], the range is [latex]\left(-\infty ,\infty \right)\\[/latex], and the vertical asymptote is x = 0.
Graph of f(x)=log_(1/5)(x) with labeled points at (1/5, 1) and (1, 0). The y-axis is the asymptote.

4. The domain is [latex]\left(-4,\infty \right)\\[/latex], the range [latex]\left(-\infty ,\infty \right)\\[/latex], and the asymptote x = –4.
Graph of two functions. The parent function is y=log_3(x), with an asymptote at x=0 and labeled points at (1, 0), and (3, 1).The translation function f(x)=log_3(x+4) has an asymptote at x=-4 and labeled points at (-3, 0) and (-1, 1).

5. The domain is [latex]\left(0,\infty \right)\\[/latex], the range is [latex]\left(-\infty ,\infty \right)\\[/latex], and the vertical asymptote is x = 0.
Graph of two functions. The parent function is y=log_2(x), with an asymptote at x=0 and labeled points at (1, 0), and (2, 1).The translation function f(x)=log_2(x)+2 has an asymptote at x=0 and labeled points at (0.25, 0) and (0.5, 1).

6. The domain is [latex]\left(0,\infty \right)\\[/latex], the range is [latex]\left(-\infty ,\infty \right)\\[/latex], and the vertical asymptote is x = 0.
Graph of two functions. The parent function is y=log_4(x), with an asymptote at x=0 and labeled points at (1, 0), and (4, 1).The translation function f(x)=(1/2)log_4(x) has an asymptote at x=0 and labeled points at (1, 0) and (16, 1).

7. The domain is [latex]\left(2,\infty \right)\\[/latex], the range is [latex]\left(-\infty ,\infty \right)\\[/latex], and the vertical asymptote is x = 2.

Graph of f(x)=3log(x-2)+1 with an asymptote at x=2.

8. The domain is [latex]\left(-\infty ,0\right)\\[/latex], the range is [latex]\left(-\infty ,\infty \right)\\[/latex], and the vertical asymptote is x = 0.
Graph of f(x)=-log(-x) with an asymptote at x=0.

9. [latex]x\approx 3.049\\[/latex]

10. x = 1

11. [latex]f\left(x\right)=2\mathrm{ln}\left(x+3\right)-1\\[/latex]

Solutions to Odd-Numbered Exercises

1. Since the functions are inverses, their graphs are mirror images about the line y = x. So for every point [latex]\left(a,b\right)\\[/latex] on the graph of a logarithmic function, there is a corresponding point [latex]\left(b,a\right)\\[/latex] on the graph of its inverse exponential function.

3. Shifting the function right or left and reflecting the function about the y-axis will affect its domain.

5. No. A horizontal asymptote would suggest a limit on the range, and the range of any logarithmic function in general form is all real numbers.

7. Domain: [latex]\left(-\infty ,\frac{1}{2}\right)\\[/latex]; Range: [latex]\left(-\infty ,\infty \right)\\[/latex]

9. Domain: [latex]\left(-\frac{17}{4},\infty \right)\\[/latex]; Range: [latex]\left(-\infty ,\infty \right)\\[/latex]

11. Domain: [latex]\left(5,\infty \right)\\[/latex]; Vertical asymptote: x = 5

13. Domain: [latex]\left(-\frac{1}{3},\infty \right)\\[/latex]; Vertical asymptote: [latex]x=-\frac{1}{3}\\[/latex]

15. Domain: [latex]\left(-3,\infty \right)\\[/latex]; Vertical asymptote: x = –3

17. Domain: [latex]\left(\frac{3}{7},\infty \right)\\[/latex]; Vertical asymptote: [latex]x=\frac{3}{7}\\[/latex] ; End behavior: as [latex]x\to {\left(\frac{3}{7}\right)}^{+},f\left(x\right)\to -\infty \\[/latex] and as [latex]x\to \infty ,f\left(x\right)\to \infty \\[/latex]

19. Domain: [latex]\left(-3,\infty \right)\\[/latex] ; Vertical asymptote: x = –3; End behavior: as [latex]x\to -{3}^{+}\\[/latex] , [latex]f\left(x\right)\to -\infty \\[/latex] and as [latex]x\to \infty \\[/latex] , [latex]f\left(x\right)\to \infty \\[/latex]

21. Domain: [latex]\left(1,\infty \right)\\[/latex]; Range: [latex]\left(-\infty ,\infty \right)\\[/latex]; Vertical asymptote: x = 1; x-intercept: [latex]\left(\frac{5}{4},0\right)\\[/latex]; y-intercept: DNE

23. Domain: [latex]\left(-\infty ,0\right)\\[/latex]; Range: [latex]\left(-\infty ,\infty \right)\\[/latex]; Vertical asymptote: x = 0; x-intercept: [latex]\left(-{e}^{2},0\right)\\[/latex]; y-intercept: DNE

25. Domain: [latex]\left(0,\infty \right)\\[/latex]; Range: [latex]\left(-\infty ,\infty \right)\\[/latex]; Vertical asymptote: x = 0; x-intercept: [latex]\left({e}^{3},0\right)[/latex]; y-intercept: DNE

27. B

29. C

31. B

33. C

35.
Graph of two functions, g(x) = log_(1/2)(x) in orange and f(x)=log(x) in blue.

37.
Graph of two functions, g(x) = ln(1/2)(x) in orange and f(x)=e^(x) in blue.

39. C

41.
Graph of f(x)=log_2(x+2).

43.
Graph of f(x)=ln(-x).

45.
Graph of g(x)=log(6-3x)+1.

47. [latex]f\left(x\right)={\mathrm{log}}_{2}\left(-\left(x - 1\right)\right)\\[/latex]

49. [latex]f\left(x\right)=3{\mathrm{log}}_{4}\left(x+2\right)\\[/latex]

51. x = 2

53. [latex]x\approx \text{2}\text{.303}\\[/latex]

55. [latex]x\approx -0.472\\[/latex]

57. The graphs of [latex]f\left(x\right)={\mathrm{log}}_{\frac{1}{2}}\left(x\right)\\[/latex] and [latex]g\left(x\right)=-{\mathrm{log}}_{2}\left(x\right)\\[/latex] appear to be the same; Conjecture: for any positive base [latex]b\ne 1\\[/latex], [latex]{\mathrm{log}}_{b}\left(x\right)=-{\mathrm{log}}_{\frac{1}{b}}\left(x\right)\\[/latex].

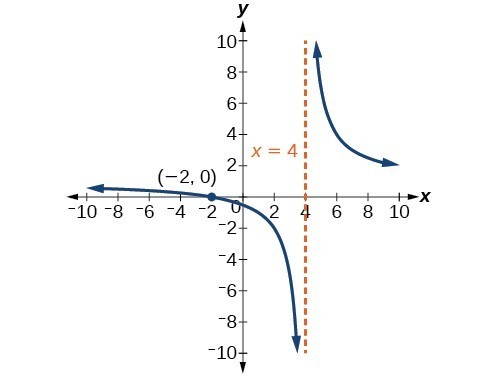
59. Recall that the argument of a logarithmic function must be positive, so we determine where [latex]\frac{x+2}{x - 4}>0\\[/latex] . From the graph of the function [latex]f\left(x\right)=\frac{x+2}{x - 4}\\[/latex], note that the graph lies above the x-axis on the interval [latex]\left(-\infty ,-2\right)\\[/latex] and again to the right of the vertical asymptote, that is [latex]\left(4,\infty \right)\\[/latex]. Therefore, the domain is [latex]\left(-\infty ,-2\right)\cup \left(4,\infty \right)\\[/latex].