Learning Outcomes
- Use the substitution method
- Solve a system of equations using the substitution method.
- Recognize systems of equations that have no solution or an infinite number of solutions
- Use the elimination method without multiplication
- Solve a system of equations when no multiplication is necessary to eliminate a variable
- Use the elimination method with multiplication
- Use multiplication in combination with the elimination method to solve a system of linear equations
- Recognize when the solution to a system of linear equations implies there are an infinite number of solutions
Solve a system of equations using the substitution method
In the last couple sections, we verified that ordered pairs were solutions to systems, and we used graphs to classify how many solutions a system of two linear equations had. What if we are not given a point of intersection, or it is not obvious from a graph? Can we still find a solution to the system? Of course you can, using algebra!
In this section we will learn the substitution method for finding a solution to a system of linear equations in two variables. We have used substitution in different ways throughout this course, for example when we were using the formulas for the area of a triangle and simple interest. We substituted values that we knew into the formula to solve for values that we did not know. The idea is similar when applied to solving systems, there are just a few different steps in the process. You will first solve for one variable, and then substitute that expression into the other equation. Let’s start with an example to see what this means.
Example
Find the value of x for this system.
Equation A: [latex]4x+3y=−14[/latex]
Equation B: [latex]y=2[/latex]
You can substitute a value for a variable even if it is an expression. Here’s an example.
Example
Solve for x and y.
Equation A: [latex]y+x=3[/latex]
Equation B: [latex]x=y+5[/latex]
Remember, a solution to a system of equations must be a solution to each of the equations within the system. The ordered pair [latex](4,−1)[/latex] does work for both equations, so you know that it is a solution to the system as well.
Let’s look at another example whose substitution involves the distributive property.
Example
Solve for x and y.
[latex]\begin{array}{l}y = 3x + 6\\−2x + 4y = 4\end{array}[/latex]
In the examples above, one of the equations was already given to us in terms of the variable x or y. This allowed us to quickly substitute that value into the other equation and solve for one of the unknowns.
Sometimes you may have to rewrite one of the equations in terms of one of the variables first before you can substitute. In the example below, you will first need to isolate one of the variables before you can substitute it into the other equation.
Example
Solve for x and y.
[latex]\begin{array}{r}2x+3y=22\\3x+y=19\end{array}[/latex]
In the following video, you will be given an example of solving a systems of two equations using the substitution method.
If you had chosen the other equation to start with in the previous example, you would still be able to find the same solution. It is really a matter of preference because sometimes solving for a variable will result in having to work with fractions. As you become more experienced with algebra, you will be able to anticipate what choices will lead to more desirable outcomes.
Recognize systems of equations that have no solution or an infinite number of solutions
When we learned methods for solving linear equations in one variable, we found that some equations didn’t have any solutions, and others had an infinite number of solutions. We saw this behavior again when we started describing solutions to systems of equations in two variables.
Recall this example from Module 1 for solving linear equations in one variable:
Solve for x. [latex]12+2x–8=7x+5–5x[/latex]
[latex]\displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\end{array}[/latex]
[latex]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\,\,\,\,\,\,\,\underline{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\,\,\,}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4= \,5\end{array}[/latex]
This false statement implies there are no solutions to this equation. In the same way, you may see an outcome like this when you use the substitution method to find a solution to a system of linear equations in two variables. In the next example, you will see an example of a system of two equations that does not have a solution.
Example
Solve for x and y.
[latex]\begin{array}{l}y=5x+4\\10x−2y=4\end{array}[/latex]
You get the false statement [latex]−8=4[/latex]. What does this mean? The graph of this system sheds some light on what is happening.
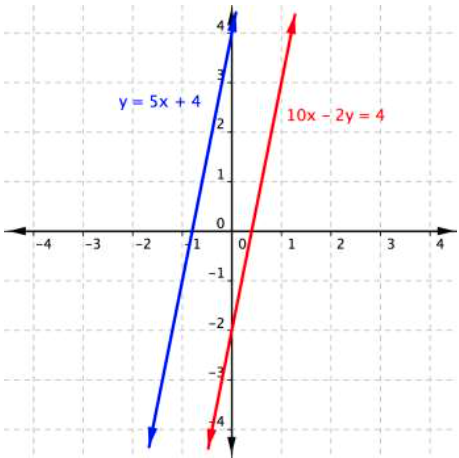
The lines are parallel, they never intersect and there is no solution to this system of linear equations. Note that the result [latex]−8=4[/latex] is not a solution. It is simply a false statement and it indicates that there is no solution.
We have also seen linear equations in one variable and systems of equations in two variables that have an infinite number of solutions. In the next example, you will see what happens when you apply the substitution method to a system with an infinite number of solutions.
Example
Solve for x and y.
[latex]\begin{array}{l}\,\,\,y=−0.5x\\9y=−4.5x\end{array}[/latex]
This time you get a true statement: [latex]−4.5x=−4.5x[/latex]. But what does this type of answer mean? Again, graphing can help you make sense of this system.
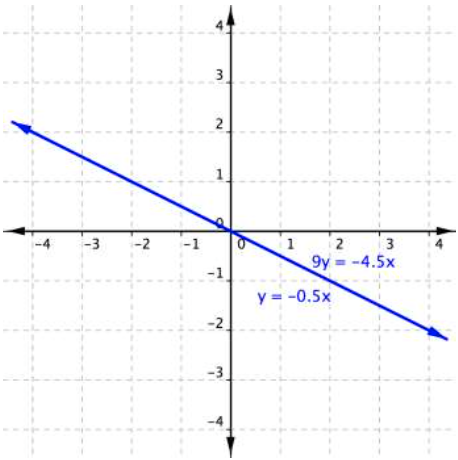
This system consists of two equations that both represent the same line; the two lines are collinear. Every point along the line will be a solution to the system, and that’s why the substitution method yields a true statement. In this case, there are an infinite number of solutions.
In the following video you will see an example of solving a system that has an infinite number of solutions.
In the following video you will see an example of solving a system of equations that has no solutions.
Solve a system of equations using the elimination method
The elimination method for solving systems of linear equations uses the addition property of equality. You can add the same value to each side of an equation to eliminate one of the variable terms. In this method, you may or may not need to multiply the terms in one equation by a number first. We will first look at examples where no multiplication is necessary to use the elimination method. In the next section you will see examples using multiplication after you are familiar with the idea of the elimination method.
It is easier to show rather than tell with this method, so let’s dive right into some examples.
If you add the two equations,
[latex]x–y=−6[/latex] and [latex]x+y=8[/latex] together, watch what happens.
[latex]\displaystyle \begin{array}{l}\,\,\,\,\,x-y=\,-6\\\underline{+\,x+y=\,\,\,8}\\\,2x+0\,=\,\,\,\,2\end{array}[/latex]
You have eliminated the y term, and this equation can be solved using the methods for solving equations with one variable.
Let’s see how this system is solved using the elimination method.
Example
Use elimination to solve the system.
[latex]\begin{array}{r}x–y=−6\\x+y=\,\,\,\,8\end{array}[/latex]
Unfortunately not all systems work out this easily. How about a system like [latex]2x+y=12[/latex] and [latex]−3x+y=2[/latex]. If you add these two equations together, no variables are eliminated.
[latex]\displaystyle \begin{array}{l}\,\,\,\,2x+y=12\\\underline{-3x+y=\,\,\,2}\\-x+2y=14\end{array}[/latex]
But you want to eliminate a variable. So let’s add the opposite of one of the equations to the other equation. This means multiply every term in one of the equations by -1, so that the sign of every terms is opposite.
[latex]\begin{array}{l}\,\,\,\,2x+\,\,y\,=12\rightarrow2x+y=12\rightarrow2x+y=12\\−3x+\,\,y\,=2\rightarrow−\left(−3x+y\right)=−(2)\rightarrow3x–y=−2\\\,\,\,\,5x+0y=10\end{array}[/latex]
You have eliminated the y variable, and the problem can now be solved.
The following video describe a similar problem where you can eliminate one variable by adding the two equations together.
 Caution! When you add the opposite of one entire equation to another, make sure to change the sign of EVERY term on both sides of the equation. This is a very common mistake to make.
Caution! When you add the opposite of one entire equation to another, make sure to change the sign of EVERY term on both sides of the equation. This is a very common mistake to make.Example
Use elimination to solve the system.
[latex]\begin{array}{r}2x+y=12\\−3x+y=2\,\,\,\end{array}[/latex]
The following are two more examples showing how to solve linear systems of equations using elimination.
Example
Use elimination to solve the system.
[latex]\begin{array}{r}−2x+3y=−1\\2x+5y=\,25\end{array}[/latex]
Example
Use elimination to solve for x and y.
[latex]\begin{array}{r}4x+2y=14\\5x+2y=16\end{array}[/latex]
Go ahead and check this last example—substitute (2, 3) into both equations. You get two true statements: 14=14 and 16=16!
Notice that you could have used the opposite of the first equation rather than the second equation and gotten the same result.
Recognize systems that have no solution or an infinite number of solutions
Just as with the substitution method, the elimination method will sometimes eliminate both variables, and you end up with either a true statement or a false statement. Recall that a false statement means that there is no solution.
Let’s look at an example.
Example
Solve for x and y.
[latex]\begin{array}{r}-x–y=-4\\x+y=2\,\,\,\,\end{array}[/latex]
Graphing these lines shows that they are parallel lines and as such do not share any point in common, verifying that there is no solution.
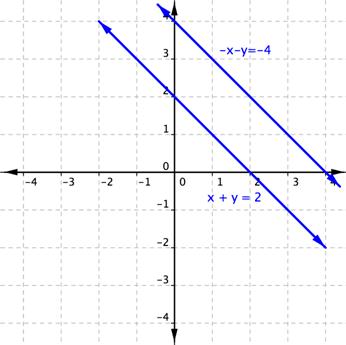
If both variables are eliminated and you are left with a true statement, this indicates that there are an infinite number of ordered pairs that satisfy both of the equations. In fact, the equations are the same line.
Example
Solve for x and y.
[latex]\begin{array}{r}x+y=2\,\,\,\,\\-x−y=-2\end{array}[/latex]
Graphing these two equations will help to illustrate what is happening.

In the following video, a system of equations which has no solutions is solved using the method of elimination.
Solve a system of equations when multiplication is necessary to eliminate a variable
Many times adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Look at the system below.
[latex]\begin{array}{r}3x+4y=52\\5x+y=30\end{array}[/latex]
If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. So let’s now use the multiplication property of equality first. You can multiply both sides of one of the equations by a number that will allow you to eliminate the same variable in the other equation.
We do this with multiplication. Notice that the first equation contains the term 4y, and the second equation contains the term y. If you multiply the second equation by −4, when you add both equations the y variables will add up to 0.
The following example takes you through all the steps to find a solution to this system.
Example
Solve for x and y.
Equation A: [latex]3x+4y=52[/latex]
Equation B: [latex]5x+y=30[/latex]
There are other ways to solve this system. Instead of multiplying one equation in order to eliminate a variable when the equations were added, you could have multiplied both equations by different numbers.
Let’s remove the variable x this time. Multiply Equation A by 5 and Equation B by [latex]−3[/latex].
Example
Solve for x and y.
[latex]\begin{array}{r}3x+4y=52\\5x+y=30\end{array}[/latex]
These equations were multiplied by 5 and [latex]−3[/latex] respectively, because that gave you terms that would add up to 0. Be sure to multiply all of the terms of the equation.
In the following video, you will see an example of using the elimination method for solving a system of equations.
It is possible to use the elimination method with multiplication and get a result that indicates no solutions or infinitely many solutions, just as with the other methods we have learned for finding solutions to systems. In the following example, you will see a system that has infinitely many solutions.
Example
Solve for x and y.
Equation A: [latex]x-3y=-2[/latex]
Equation B: [latex]-2x+6y=4[/latex]
In the following video, the elimination method is used to solve a system of equations. Notice that one of the equations needs to be multiplied by a negative one first. Additionally, this system has an infinite number of solutions.
Summary
The substitution method is one way of solving systems of equations. To use the substitution method, use one equation to find an expression for one of the variables in terms of the other variable. Then substitute that expression in place of that variable in the second equation. You can then solve this equation as it will now have only one variable. Solving using the substitution method will yield one of three results: a single value for each variable within the system (indicating one solution), an untrue statement (indicating no solutions), or a true statement (indicating an infinite number of solutions).
Combining equations is a powerful tool for solving a system of equations. Adding or subtracting two equations in order to eliminate a common variable is called the elimination (or addition) method. Once one variable is eliminated, it becomes much easier to solve for the other one.
Multiplication can be used to set up matching terms in equations before they are combined to aid in finding a solution to a system. When using the multiplication method, it is important to multiply all the terms on both sides of the equation—not just the one term you are trying to eliminate.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex 2: Solve a System of Equations Using Substitution. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/MIXL35YRzRw. License: CC BY: Attribution
- Ex: Solve a System of Equations Using Substitution - Infinite Solutions. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/Pcqb109yK5Q. License: CC BY: Attribution
- Ex: Solve a System of Equations Using Substitution - No Solution. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/kTtKfh5gFUc. License: All Rights Reserved
- Unit 13: Graphing, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
- Ex 1: Solve a System of Equations Using the Elimination Method . Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/M4IEmwcqR3c. License: CC BY: Attribution
- Ex 2: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/_liDhKops2w. License: CC BY: Attribution
- Ex: System of Equations Using Elimination (Infinite Solutions) . Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/NRxh9Q16Ulk. License: CC BY: Attribution
- Ex: System of Equations Using Elimination (Infinite Solutions). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/NRxh9Q16Ulk. License: CC BY: Attribution
- Ex 2: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/_liDhKops2w. License: CC BY: Attribution