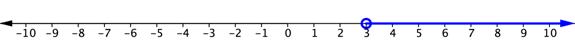Learning Outcomes
- Describe sets as intersections or unions
- Use interval notation to describe intersections and unions
- Use graphs to describe intersections and unions
- Solve compound inequalities—OR
- Solve compound inequalities in the form of or and express the solution graphically and with an interval
- Solve compound inequalities—AND
- Express solutions to inequalities graphically and with interval notation
- Identify solutions for compound inequalities in the form [latex]a<x<b[/latex], including cases with no solution
- Solve absolute value inequalities
- Solve single- and multi-step inequalities containing absolute values
- Identify cases where there are no solutions to absolute value inequalities
Use interval notation to describe sets of numbers as intersections and unions
When two inequalities are joined by the word and, the solution of the compound inequality occurs when both inequalities are true at the same time. It is the overlap, or intersection, of the solutions for each inequality. When the two inequalities are joined by the word or, the solution of the compound inequality occurs when either of the inequalities is true. The solution is the combination, or union, of the two individual solutions.
In this section we will learn how to solve compound inequalities that are joined with the words AND and OR. First, it will help to see some examples of inequalities, intervals, and graphs of compound inequalities. This will help you describe the solutions to compound inequalities properly.
Venn diagrams use the concept of intersections and unions to show how much two or more things share in common. For example, this Venn diagram shows the intersection of people who are breaking your heart and those who are shaking your confidence daily. Apparently Cecilia has both of these qualities; therefore she is the intersection of the two.

In mathematical terms, consider the inequality [latex]x\lt6[/latex] and [latex]x\gt2[/latex]. How would we interpret what numbers x can be, and what would the interval look like?
In words, x must be less than 6 and at the same time, it must be greater than 2, much like the Venn diagram above, where Cecilia is at once breaking your heart and shaking your confidence daily. Let’s look at a graph to see what numbers are possible with these constraints.

The numbers that are shared by both lines on the graph are called the intersection of the two inequalities [latex]x\lt6[/latex] and [latex]x\gt2[/latex]. This is called a bounded inequality and is written as [latex]2\lt{x}\lt6[/latex]. Think about that one for a minute. x must be less than 6 and greater than two—the values for x will fall between two numbers. In interval notation, this looks like [latex]\left(2,6\right)[/latex]. The graph would look like this:

On the other hand, if you need to represent two things that don’t share any common elements or traits, you can use a union. The following Venn diagram shows two things that share no similar traits or elements but are often considered in the same application, such as online shopping or banking.

In mathematical terms, for example, [latex]x>6[/latex] or [latex]x<2[/latex] is an inequality joined by the word or. Using interval notation, we can describe each of these inequalities separately:
[latex]x\gt6[/latex] is the same as [latex]\left(6, \infty\right)[/latex] and [latex]x<2[/latex] is the same as [latex]\left(\infty, 2\right)[/latex]. If we are describing solutions to inequalities, what effect does the or have? We are saying that solutions are either real numbers less than two or real numbers greater than 6. Can you see why we need to write them as two separate intervals? Let’s look at a graph to get a clear picture of what is going on.

When you place both of these inequalities on a graph, we can see that they share no numbers in common. This is what we call a union, as mentioned above. The interval notation associated with a union is a big U, so instead of writing or, we join our intervals with a big U, like this:
[latex]\left(\infty, 2\right)\cup\left(6, \infty\right)[/latex]
It is common convention to construct intervals starting with the value that is furthest left on the number line as the left value, such as [latex]\left(2,6\right)[/latex], where 2 is less than 6. The number on the right should be greater than the number on the left.
Example
Draw the graph of the compound inequality [latex]x\gt3[/latex] or [latex]x\le4[/latex] and describe the set of x-values that will satisfy it with an interval.
In the following video you will see two examples of how to express inequalities involving OR graphically and as an interval.
Examples
Draw a graph of the compound inequality: [latex]x\lt5[/latex] and [latex]x\ge−1[/latex], and describe the set of x-values that will satisfy it with an interval.
Examples
Draw the graph of the compound inequality [latex]x\lt{-3}[/latex] and [latex]x\gt{3}[/latex], and describe the set of x-values that will satisfy it with an interval.
The following video presents two examples of how to draw inequalities involving AND, as well as write the corresponding intervals.
Solve compound inequalities in the form of or
As we saw in the last section, the solution of a compound inequality that consists of two inequalities joined with the word or is the union of the solutions of each inequality. Unions allow us to create a new set from two that may or may not have elements in common.
In this section you will see that some inequalities need to be simplified before their solution can be written or graphed.
In the following example, you will see an example of how to solve a one-step inequality in the OR form. Note how each inequality is treated independently until the end where the solution is described in terms of both inequalities. You will use the same properties to solve compound inequalities that you used to solve regular inequalities.
Example
Solve for x. [latex]3x–1<8[/latex] or [latex]x–5>0[/latex]
Remember to apply the properties of inequality when you are solving compound inequalities. The next example involves dividing by a negative to isolate a variable.
Example
Solve for y. [latex]2y+7\lt13\text{ or }−3y–2\lt10[/latex]
In the last example, the final answer included solutions whose intervals overlapped, causing the answer to include all the numbers on the number line. In words, we call this solution “all real numbers.” Any real number will produce a true statement for either [latex]y<3\text{ or }y\ge -4[/latex], when it is substituted for x.
Example
Solve for z. [latex]5z–3\gt−18[/latex] or [latex]−2z–1\gt15[/latex]
The following video contains an example of solving a compound inequality involving OR, and drawing the associated graph.
In the next section you will see examples of how to solve compound inequalities containing and.
Solve compound inequalities in the form of and and express the solution graphically
The solution of a compound inequality that consists of two inequalities joined with the word and is the intersection of the solutions of each inequality. In other words, both statements must be true at the same time. The solution to an and compound inequality are all the solutions that the two inequalities have in common. As we saw in the last sections, this is where the two graphs overlap.
In this section we will see more examples where we have to simplify the compound inequalities before we can express their solutions graphically or with an interval.
Example
Solve for x. [latex] \displaystyle 1-4x\le 21\,\,\,\,\text{and}\,\,\,\,5x+2\ge22[/latex]
Example
Solve for x: [latex] \displaystyle {5}{x}-{2}\le{3}\text{ and }{4}{x}{+7}>{3}[/latex]
Compound inequalities in the form [latex]a<x<b[/latex]
Rather than splitting a compound inequality in the form of [latex]a<x<b[/latex] into two inequalities [latex]x<b[/latex] and [latex]x>a[/latex], you can more quickly to solve the inequality by applying the properties of inequality to all three segments of the compound inequality.
Example
Solve for x. [latex]3\lt2x+3\leq 7[/latex]
In the video below, you will see another example of how to solve an inequality in the form [latex]a<x<b[/latex]
To solve inequalities like [latex]a<x<b[/latex], use the addition and multiplication properties of inequality to solve the inequality for x. Whatever operation you perform on the middle portion of the inequality, you must also perform to each of the outside sections as well. Pay particular attention to division or multiplication by a negative.
The solution to a compound inequality with and is always the overlap between the solution to each inequality. There are three possible outcomes for compound inequalities joined by the word and:
| Case 1: | |
|---|---|
| Description | The solution could be all the values between two endpoints |
| Inequalities | [latex]x\le{1}[/latex] and [latex]x\gt{-1}[/latex], or as a bounded inequality: [latex]{-1}\lt{x}\le{1}[/latex] |
| Interval | [latex]\left(-1,1\right][/latex] |
| Graphs |

|
| Case 2: | |
| Description | The solution could begin at a point on the number line and extend in one direction. |
| Inequalities | [latex]x\gt3[/latex] and [latex]x\ge4[/latex] |
| Interval | [latex]\left[4,\infty\right)[/latex] |
| Graphs |
|
| Case 3: | |
| Description | In cases where there is no overlap between the two inequalities, there is no solution to the compound inequality |
| Inequalities | [latex]x\lt{-3}[/latex] and [latex]x\gt{3}[/latex] |
| Intervals | [latex]\left(-\infty,-3\right)[/latex] and [latex]\left(3,\infty\right)[/latex] |
| Graph |  |
In the example below, there is no solution to the compound inequality because there is no overlap between the inequalities.
Example
Solve for x. [latex]x+2>5[/latex] and [latex]x+4<5[/latex]
Solve inequalities containing absolute values
Let’s apply what you know about solving equations that contain absolute values and what you know about inequalities to solve inequalities that contain absolute values. Let’s start with a simple inequality.
[latex]\left|x\right|\leq 4[/latex]
This inequality is read, “the absolute value of x is less than or equal to 4.” If you are asked to solve for x, you want to find out what values of x are 4 units or less away from 0 on a number line. You could start by thinking about the number line and what values of x would satisfy this equation.
4 and [latex]−4[/latex] are both four units away from 0, so they are solutions. 3 and [latex]−3[/latex] are also solutions because each of these values is less than 4 units away from 0. So are 1 and [latex]−1[/latex], 0.5 and [latex]−0.5[/latex], and so on—there are an infinite number of values for x that will satisfy this inequality.
The graph of this inequality will have two closed circles, at 4 and [latex]−4[/latex]. The distance between these two values on the number line is colored in blue because all of these values satisfy the inequality.

The solution can be written this way:
Inequality: [latex]-4\leq x\leq4[/latex]
Interval: [latex]\left[-4,4\right][/latex]
The situation is a little different when the inequality sign is “greater than” or “greater than or equal to.” Consider the simple inequality [latex]\left|x\right|>3[/latex]. Again, you could think of the number line and what values of x are greater than 3 units away from zero. This time, 3 and [latex]−3[/latex] are not included in the solution, so there are open circles on both of these values. 2 and [latex]−2[/latex] would not be solutions because they are not more than 3 units away from 0. But 5 and [latex]−5[/latex] would work, and so would all of the values extending to the left of [latex]−3[/latex] and to the right of 3. The graph would look like the one below.

The solution to this inequality can be written this way:
Inequality: [latex]x<−3[/latex] or [latex]x>3[/latex].
Interval: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex]
In the following video, you will see examples of how to solve and express the solution to absolute value inequalities involving both AND and OR.
Writing Solutions to Absolute Value Inequalities
For any positive value of a and x, a single variable, or any algebraic expression:
| Absolute Value Inequality | Equivalent Inequality | Interval Notation |
| [latex]\left|{ x }\right|\le{ a}[/latex] | [latex]{ -a}\le{x}\le{ a}[/latex] | [latex]\left[-a, a\right][/latex] |
| [latex]\left| x \right|\lt{a}[/latex] | [latex]{ -a}\lt{x}\lt{ a}[/latex] | [latex]\left(-a, a\right)[/latex] |
| [latex]\left| x \right|\ge{ a}[/latex] | [latex]{x}\le\text{−a}[/latex] or [latex]{x}\ge{ a}[/latex] | [latex]\left(-\infty,-a\right]\cup\left[a,\infty\right)[/latex] |
| [latex]\left| x \right|\gt\text{a}[/latex] | [latex]\displaystyle{x}\lt\text{−a}[/latex] or [latex]{x}\gt{ a}[/latex] | [latex]\left(-\infty,-a\right)\cup\left(a,\infty\right)[/latex] |
Let’s look at a few more examples of inequalities containing absolute values.
Example
Solve for x. [latex]\left|x+3\right|\gt4[/latex]
Example
Solve for y. [latex] \displaystyle \mathsf{3}\left| \mathsf{2}\mathrm{y}\mathsf{+6} \right|-\mathsf{9<27}[/latex]
In the following video, you will see an example of solving multi-step absolute value inequalities involving an OR situation.
In the following video you will see an example of solving multi-step absolute value inequalities involving an AND situation.
In the last video that follows, you will see an example of solving an absolute value inequality where you need to isolate the absolute value first.
Identify cases of inequalities containing absolute values that have no solutions
As with equations, there may be instances in which there is no solution to an inequality.
Example
Solve for x. [latex]\left|2x+3\right|+9\leq 7[/latex]
Summary
A compound inequality is a statement of two inequality statements linked together either by the word or or by the word and. Sometimes, an and compound inequality is shown symbolically, like [latex]a<x<b[/latex], and does not even need the word and. Because compound inequalities represent either a union or intersection of the individual inequalities, graphing them on a number line can be a helpful way to see or check a solution. Compound inequalities can be manipulated and solved in much the same way any inequality is solved, by paying attention to the properties of inequalities and the rules for solving them.
Absolute inequalities can be solved by rewriting them using compound inequalities. The first step to solving absolute inequalities is to isolate the absolute value. The next step is to decide whether you are working with an OR inequality or an AND inequality. If the inequality is greater than a number, we will use OR. If the inequality is less than a number, we will use AND. Remember that if we end up with an absolute value greater than or less than a negative number, there is no solution.