Exponential and Logarithmic Functions

Learning Outcomes

  • Recognize the derivative and integral of the exponential function.
  • Prove properties of logarithms and exponential functions using integrals.
  • Express general logarithmic and exponential functions in terms of natural logarithms and exponentials.

The Exponential Function

We now turn our attention to the function [latex]{e}^{x}.[/latex] Note that the natural logarithm is one-to-one and therefore has an inverse function. For now, we denote this inverse function by [latex]\text{exp}x.[/latex] Then,

[latex]\text{exp}(\text{ln}x)=x\text{ for }x>0\text{ and }\text{ln}(\text{exp}x)=x\text{ for all }x.[/latex]

 

The following figure shows the graphs of [latex]\text{exp}x[/latex] and [latex]\text{ln}x.[/latex]

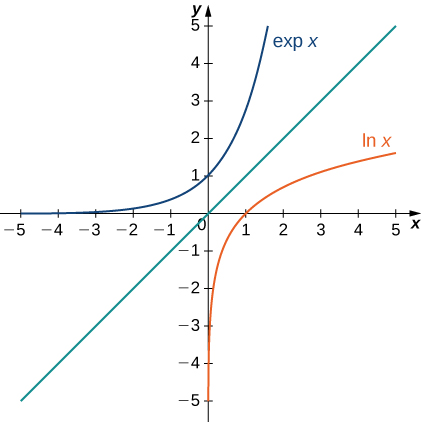
This figure is a graph. It has three curves. The first curve is labeled exp x. It is an increasing curve with the x-axis as a horizontal asymptote. It intersects the y-axis at y=1. The second curve is a diagonal line through the origin. The third curve is labeled lnx. It is an increasing curve with the y-axis as an vertical axis. It intersects the x-axis at x=1.

Figure 4. The graphs of [latex]\text{ln}x[/latex] and [latex]\text{exp}x.[/latex]

We hypothesize that [latex]\text{exp}x={e}^{x}.[/latex] For rational values of [latex]x,[/latex] this is easy to show. If [latex]x[/latex] is rational, then we have [latex]\text{ln}({e}^{x})=x\text{ln}e=x.[/latex] Thus, when [latex]x[/latex] is rational, [latex]{e}^{x}=\text{exp}x.[/latex] For irrational values of [latex]x,[/latex] we simply define [latex]{e}^{x}[/latex] as the inverse function of [latex]\text{ln}x.[/latex]

Definition

For any real number [latex]x,[/latex] define [latex]y={e}^{x}[/latex] to be the number for which

[latex]\text{ln}y=\text{ln}({e}^{x})=x[/latex]

 

Then we have [latex]{e}^{x}=\text{exp}(x)[/latex] for all [latex]x,[/latex] and thus

[latex]{e}^{\text{ln}x}=x\text{ for }x>0\text{ and }\text{ln}({e}^{x})=x[/latex]

 

for all [latex]x.[/latex]

Properties of the Exponential Function

Since the exponential function was defined in terms of an inverse function, and not in terms of a power of [latex]e,[/latex] we must verify that the usual laws of exponents hold for the function [latex]{e}^{x}.[/latex]

Properties of the Exponential Function

If [latex]p[/latex] and [latex]q[/latex] are any real numbers and [latex]r[/latex] is a rational number, then

  1. [latex]{e}^{p}{e}^{q}={e}^{p+q}[/latex]
  2. [latex]\frac{{e}^{p}}{{e}^{q}}={e}^{p-q}[/latex]
  3. [latex]{({e}^{p})}^{r}={e}^{pr}[/latex]

Proof

Note that if [latex]p[/latex] and [latex]q[/latex] are rational, the properties hold. However, if [latex]p[/latex] or [latex]q[/latex] are irrational, we must apply the inverse function definition of [latex]{e}^{x}[/latex] and verify the properties. Only the first property is verified here; the other two are left to you. We have

[latex]\text{ln}({e}^{p}{e}^{q})=\text{ln}({e}^{p})+\text{ln}({e}^{q})=p+q=\text{ln}({e}^{p+q}).[/latex]

 

Since [latex]\text{ln}x[/latex] is one-to-one, then

[latex]{e}^{p}{e}^{q}={e}^{p+q}.[/latex]

[latex]_\blacksquare[/latex]

As with part iv. of the logarithm properties, we can extend property iii. to irrational values of [latex]r,[/latex] and we do so by the end of the section.

We also want to verify the differentiation formula for the function [latex]y={e}^{x}.[/latex] To do this, we need to use implicit differentiation. Let [latex]y={e}^{x}.[/latex] Then

[latex]\begin{array}{ccc}\hfill \text{ln}y& =\hfill & x\hfill \\ \hfill \frac{d}{dx}\text{ln}y& =\hfill & \frac{d}{dx}x\hfill \\ \hfill \frac{1}{y}\frac{dy}{dx}& =\hfill & 1\hfill \\ \hfill \frac{dy}{dx}& =\hfill & y.\hfill \end{array}[/latex]

 

Thus, we see

[latex]\frac{d}{dx}{e}^{x}={e}^{x}[/latex]

 

as desired, which leads immediately to the integration formula

[latex]\displaystyle\int {e}^{x}dx={e}^{x}+C[/latex]

 

We apply these formulas in the following examples.

Example: Using Properties of Exponential Functions

Evaluate the following derivatives:

  1. [latex]\frac{d}{dt}{e}^{3t}{e}^{{t}^{2}}[/latex]
  2. [latex]\frac{d}{dx}{e}^{3{x}^{2}}[/latex]

Try It

Evaluate the following derivatives:

  1. [latex]\frac{d}{dx}(\frac{{e}^{{x}^{2}}}{{e}^{5x}})[/latex]
  2. [latex]\frac{d}{dt}{({e}^{2t})}^{3}[/latex]

Hint

Use the properties of exponential functions and the chain rule as necessary.

Watch the following video to see the worked solution to the above Try It.

Example: Using Properties of Exponential Functions

Evaluate the following integral: [latex]\displaystyle\int 2x{e}^{\text{−}{x}^{2}}dx.[/latex]

 

Try It

Evaluate the following integral: [latex]\displaystyle\int \frac{4}{{e}^{3x}}dx.[/latex]

Hint

Use the properties of exponential functions and [latex]u\text{-substitution}[/latex] as necessary.

Watch the following video to see the worked solution to the above Try It.

Try It

General Logarithmic and Exponential Functions

We close this section by looking at exponential functions and logarithms with bases other than [latex]e.[/latex] Exponential functions are functions of the form [latex]f(x)={a}^{x}.[/latex] Note that unless [latex]a=e,[/latex] we still do not have a mathematically rigorous definition of these functions for irrational exponents. Let’s rectify that here by defining the function [latex]f(x)={a}^{x}[/latex] in terms of the exponential function [latex]{e}^{x}.[/latex] We then examine logarithms with bases other than [latex]e[/latex] as inverse functions of exponential functions.

Definition

For any [latex]a>0,[/latex] and for any real number [latex]x,[/latex] define [latex]y={a}^{x}[/latex] as follows:

[latex]y={a}^{x}={e}^{x\text{ln}a}[/latex]

 

Now [latex]{a}^{x}[/latex] is defined rigorously for all values of [latex]x[/latex]. This definition also allows us to generalize property iv. of logarithms and property iii. of exponential functions to apply to both rational and irrational values of [latex]r.[/latex] It is straightforward to show that properties of exponents hold for general exponential functions defined in this way.

Let’s now apply this definition to calculate a differentiation formula for [latex]{a}^{x}.[/latex] We have

[latex]\frac{d}{dx}{a}^{x}=\frac{d}{dx}{e}^{x\text{ln}a}={e}^{x\text{ln}a}\text{ln}a={a}^{x}\text{ln}a.[/latex]

 

The corresponding integration formula follows immediately.

Derivatives and Integrals Involving General Exponential Functions

Let [latex]a>0.[/latex] Then,

[latex]\frac{d}{dx}{a}^{x}={a}^{x}\text{ln}a[/latex]

 

and

[latex]\displaystyle\int {a}^{x}dx=\frac{1}{\text{ln}a}{a}^{x}+C[/latex]

 

If [latex]a\ne 1,[/latex] then the function [latex]{a}^{x}[/latex] is one-to-one and has a well-defined inverse. Its inverse is denoted by [latex]{\text{log}}_{a}x.[/latex] Then,

[latex]y={\text{log}}_{a}x\text{if and only if}x={a}^{y}[/latex]

 

Note that general logarithm functions can be written in terms of the natural logarithm. Let [latex]y={\text{log}}_{a}x.[/latex] Then, [latex]x={a}^{y}.[/latex] Taking the natural logarithm of both sides of this second equation, we get

[latex]\begin{array}{ccc}\hfill \text{ln}x& =\hfill & \text{ln}({a}^{y})\hfill \\ \hfill \text{ln}x& =\hfill & y\text{ln}a\hfill \\ \hfill y& =\hfill & \frac{\text{ln}x}{\text{ln}a}\hfill \\ \hfill {\text{log}}_{}x& =\hfill & \frac{\text{ln}x}{\text{ln}a}.\hfill \end{array}[/latex]

 

Thus, we see that all logarithmic functions are constant multiples of one another. Next, we use this formula to find a differentiation formula for a logarithm with base [latex]a.[/latex] Again, let [latex]y={\text{log}}_{a}x.[/latex] Then,

[latex]\begin{array}{cc}\hfill \frac{dy}{dx}& =\frac{d}{dx}({\text{log}}_{a}x)\hfill \\ & =\frac{d}{dx}(\frac{\text{ln}x}{\text{ln}a})\hfill \\ & =(\frac{1}{\text{ln}a})\frac{d}{dx}(\text{ln}x)\hfill \\ & =\frac{1}{\text{ln}a}·\frac{1}{x}\hfill \\ & =\frac{1}{x\text{ln}a}.\hfill \end{array}[/latex]

 

Derivatives of General Logarithm Functions

Let [latex]a>0.[/latex] Then,

[latex]\frac{d}{dx}{\text{log}}_{a}x=\frac{1}{x\text{ln}a}[/latex]

 

Example: Calculating Derivatives of General Exponential and Logarithm Functions

Evaluate the following derivatives:

  1. [latex]\frac{d}{dt}({4}^{t}·{2}^{{t}^{2}})[/latex]
  2. [latex]\frac{d}{dx}{\text{log}}_{8}(7{x}^{2}+4)[/latex]

Try It

Evaluate the following derivatives:

  1. [latex]\frac{d}{dt}{4}^{{t}^{4}}[/latex]
  2. [latex]\frac{d}{dx}{\text{log}}_{3}(\sqrt{{x}^{2}+1})[/latex]

Watch the following video to see the worked solution to the above Try It.

Example: Integrating General Exponential Functions

Evaluate the following integral: [latex]\displaystyle\int \frac{3}{{2}^{3x}}dx.[/latex]

 

Try It

Evaluate the following integral: [latex]\displaystyle\int {x}^{2}{2}^{{x}^{3}}dx.[/latex]

Hint

Use the properties of exponential functions and [latex]u\text{-substitution}[/latex] as necessary.

Watch the following video to see the worked solution to the above Try It.