Derivative Function Graphs

We have already discussed how to graph a function, so given the equation of a function or the equation of a derivative function, we could graph it. Given both, we would expect to see a correspondence between the graphs of these two functions, since [latex]f^{\prime}(x)[/latex] gives the rate of change of a function [latex]f(x)[/latex] (or slope of the tangent line to [latex]f(x)[/latex]). It may be useful here to recall the characteristics of lines with certain slopes.

In the first example we found that for [latex]f(x)=\sqrt{x}, \, f^{\prime}(x)=\frac{1}{2}\sqrt{x}[/latex]. If we graph these functions on the same axes, as in Figure 2, we can use the graphs to understand the relationship between these two functions. First, we notice that [latex]f(x)[/latex] is increasing over its entire domain, which means that the slopes of its tangent lines at all points are positive. Consequently, we expect [latex]f^{\prime}(x)>0[/latex] for all values of [latex]x[/latex] in its domain. Furthermore, as [latex]x[/latex] increases, the slopes of the tangent lines to [latex]f(x)[/latex] are decreasing and we expect to see a corresponding decrease in [latex]f^{\prime}(x)[/latex]. We also observe that [latex]f(0)[/latex] is undefined and that [latex]\underset{x\to 0^+}{\lim}f^{\prime}(x)=+\infty[/latex], corresponding to a vertical tangent to [latex]f(x)[/latex] at 0.

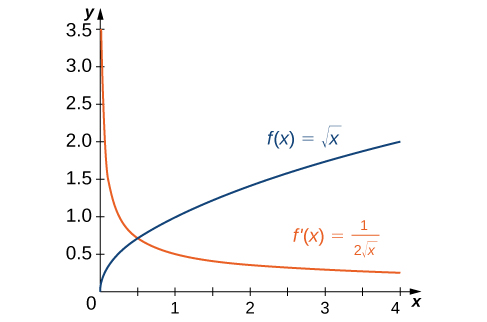
Figure 2. The derivative [latex]f^{\prime}(x)[/latex] is positive everywhere because the function [latex]f(x)[/latex] is increasing.

In the second example we found that for [latex]f(x)=x^2-2x, \, f^{\prime}(x)=2x-2[/latex]. The graphs of these functions are shown in Figure 3. Observe that [latex]f(x)[/latex] is decreasing for [latex]x<1[/latex]. For these same values of [latex]x, \, f^{\prime}(x)<0[/latex]. For values of [latex]x>1, \, f(x)[/latex] is increasing and [latex]f^{\prime}(x)>0[/latex]. Also, [latex]f(x)[/latex] has a horizontal tangent at [latex]x=1[/latex] and [latex]f^{\prime}(1)=0[/latex].

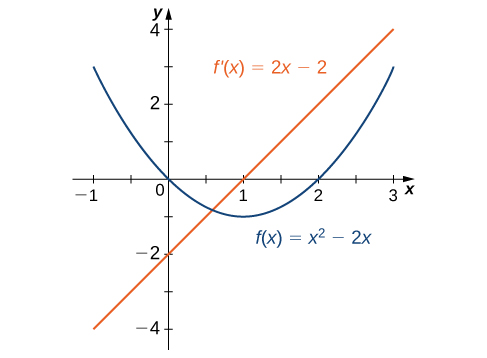
Figure 3. The derivative [latex]f^{\prime}(x)<0[/latex] where the function [latex]f(x)[/latex] is decreasing and [latex]f^{\prime}(x)>0[/latex] where [latex]f(x)[/latex] is increasing. The derivative is zero where the function has a horizontal tangent.

Example: Sketching a Derivative Using a Function

Use the following graph of [latex]f(x)[/latex] to sketch a graph of [latex]f^{\prime}(x)[/latex].

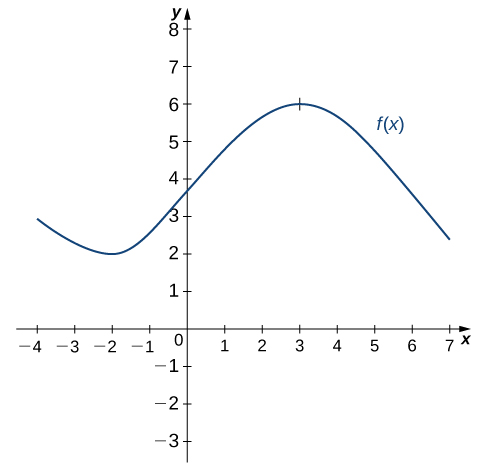
Figure 4. Graph of [latex]f(x)[/latex].

Show Solution

The solution is shown in the following graph. Observe that [latex]f(x)[/latex] is increasing and [latex]f^{\prime}(x)>0[/latex] on [latex](–2,3)[/latex]. Also, [latex]f(x)[/latex] is decreasing and [latex]f^{\prime}(x)<0[/latex] on [latex](−\infty ,-2)[/latex] and on [latex](3,+\infty)[/latex]. Also note that [latex]f(x)[/latex] has horizontal tangents at -2 and 3, and [latex]f^{\prime}(-2)=0[/latex] and [latex]f^{\prime}(3)=0[/latex].

Figure 5. Graph of [latex]f^{\prime}(x)[/latex].

Watch the following video to see the worked solution to Example: Sketching a Derivative Using a Function.

Derivatives and Continuity

Now that we can graph a derivative, let’s examine the behavior of the graphs. First, we consider the relationship between differentiability and continuity. We will see that if a function is differentiable at a point, it must be continuous there; however, a function that is continuous at a point need not be differentiable at that point. In fact, a function may be continuous at a point and fail to be differentiable at the point for one of several reasons.

Proof

If [latex]f(x)[/latex] is differentiable at [latex]a[/latex], then [latex]f^{\prime}(a)[/latex] exists and

We want to show that [latex]f(x)[/latex] is continuous at [latex]a[/latex] by showing that [latex]\underset{x\to a}{\lim}f(x)=f(a)[/latex]. Thus,

Therefore, since [latex]f(a)[/latex] is defined and [latex]\underset{x\to a}{\lim}f(x)=f(a)[/latex], we conclude that [latex]f[/latex] is continuous at [latex]a[/latex].

[latex]_\blacksquare[/latex]

We have just proven that differentiability implies continuity, but now we consider whether continuity implies differentiability. To determine an answer to this question, we examine the function [latex]f(x)=|x|[/latex]. This function is continuous everywhere; however, [latex]f^{\prime}(0)[/latex] is undefined. This observation leads us to believe that continuity does not imply differentiability. Let’s explore further. For [latex]f(x)=|x|[/latex],

This limit does not exist because

See Figure 6.

Figure 6. The function [latex]f(x)=|x|[/latex] is continuous at 0 but is not differentiable at 0.

Let’s consider some additional situations in which a continuous function fails to be differentiable. Consider the function [latex]f(x)=\sqrt[3]{x}[/latex]:

Thus [latex]f^{\prime}(0)[/latex] does not exist. A quick look at the graph of [latex]f(x)=\sqrt[3]{x}[/latex] clarifies the situation. The function has a vertical tangent line at 0 (Figure 7).

Figure 7. The function [latex]f(x)=\sqrt[3]{x}[/latex] has a vertical tangent at [latex]x=0[/latex]. It is continuous at 0 but is not differentiable at 0.

The function [latex]f(x)=\begin{cases} x \sin\left(\frac{1}{x}\right) & \text{ if } \, x \ne 0 \\ 0 & \text{ if } \, x = 0 \end{cases}[/latex] also has a derivative that exhibits interesting behavior at 0. We see that

This limit does not exist, essentially because the slopes of the secant lines continuously change direction as they approach zero (Figure 8).

Figure 8. The function [latex]f(x)=\begin{cases} x \sin(\frac{1}{x}) & \text{ if } \, x \ne 0 \\ 0 & \text{ if } \, x = 0 \end{cases}[/latex] is not differentiable at 0.

In summary:

1. We observe that if a function is not continuous, it cannot be differentiable, since every differentiable function must be continuous. However, if a function is continuous, it may still fail to be differentiable.
2. We saw that [latex]f(x)=|x|[/latex] failed to be differentiable at 0 because the limit of the slopes of the tangent lines on the left and right were not the same. Visually, this resulted in a sharp corner on the graph of the function at 0. From this we conclude that in order to be differentiable at a point, a function must be “smooth” at that point.
3. As we saw in the example of [latex]f(x)=\sqrt[3]{x}[/latex], a function fails to be differentiable at a point where there is a vertical tangent line.
4. As we saw with [latex]f(x)=\begin{cases} x \sin(\frac{1}{x}) & \text{ if } \, x \ne 0 \\ 0 & \text{ if } \, x = 0 \end{cases}[/latex] a function may fail to be differentiable at a point in more complicated ways as well.

Example: A Piecewise Function that is Continuous and Differentiable

A toy company wants to design a track for a toy car that starts out along a parabolic curve and then converts to a straight line (Figure 9). The function that describes the track is to have the form [latex]f(x)=\begin{cases} \frac{1}{10}x^2 + bx + c & \text{ if } \, x < -10 \\ -\frac{1}{4}x + \frac{5}{2} & \text{ if } \, x \ge -10 \end{cases}[/latex], where [latex]x[/latex] and [latex]f(x)[/latex] are in inches. For the car to move smoothly along the track, the function [latex]f(x)[/latex] must be both continuous and differentiable at -10. Find values of [latex]b[/latex] and [latex]c[/latex] that make [latex]f(x)[/latex] both continuous and differentiable.

Figure 9. For the car to move smoothly along the track, the function must be both continuous and differentiable.

Show Solution

For the function to be continuous at [latex]x=-10, \, \underset{x\to 10^-}{\lim}f(x)=f(-10)[/latex]. Thus, since

[latex]\underset{x\to −10^-}{\lim}f(x)=\frac{1}{10}(-10)^2-10b+c=10-10b+c[/latex]

 

and [latex]f(-10)=5[/latex], we must have [latex]10-10b+c=5[/latex]. Equivalently, we have [latex]c=10b-5[/latex].

For the function to be differentiable at -10,

[latex]f^{\prime}(10)=\underset{x\to −10}{\lim}\frac{f(x)-f(-10)}{x+10}[/latex]

 

must exist. Since [latex]f(x)[/latex] is defined using different rules on the right and the left, we must evaluate this limit from the right and the left and then set them equal to each other:

[latex]\begin{array}{lllll} \underset{x\to −10^-}{\lim}\frac{f(x)-f(-10)}{x+10} & =\underset{x\to −10^-}{\lim}\frac{\frac{1}{10}x^2+bx+c-5}{x+10} & & & \\ & =\underset{x\to −10^-}{\lim}\frac{\frac{1}{10}x^2+bx+(10b-5)-5}{x+10} & & & \text{Substitute} \, c=10b-5. \\ & =\underset{x\to −10^-}{\lim}\frac{x^2-100+10bx+100b}{10(x+10)} & & & \\ & =\underset{x\to −10^-}{\lim}\frac{(x+10)(x-10+10b)}{10(x+10)} & & & \text{Factor by grouping.} \\ & =b-2 & & & \end{array}[/latex]

 

We also have

[latex]\begin{array}{ll} \underset{x\to −10^+}{\lim}\frac{f(x)-f(-10)}{x+10} & =\underset{x\to −10^+}{\lim}\frac{-\frac{1}{4}x+\frac{5}{2}-5}{x+10} \\ & =\underset{x\to −10^+}{\lim}\frac{−(x+10)}{4(x+10)} \\ & =-\frac{1}{4} \end{array}[/latex]

 

This gives us [latex]b-2=-\frac{1}{4}[/latex].

Thus [latex]b=\frac{7}{4}[/latex] and [latex]c=10(\frac{7}{4})-5=\frac{25}{2}[/latex].

Watch the following video to see the worked solution to Example: A Piecewise Function that is Continuous and Differentiable.