Skills Review for Review of Functions

Learning Outcomes

  • Plot points on a rectangular coordinate system
  • Identify the x- and y-intercepts from the equation of a line
  • Multiply binomials – FOIL

Some of the topics covered in the Review for Functions section include drawing the graph of a function, using intercepts to graph a function, and performing operations on functions. How to plot points in the Cartesian coordinate system is reviewed here to prepare you for graphing functions. To prepare you for using intercepts to graph a function, how to find intercepts of functions is also reviewed. Finally, how to square a binomial will be discussed; this will come in handy when performing operations on functions.

Plot Points

The Cartesian coordinate system, also called the rectangular coordinate system, is based on a two-dimensional plane consisting of the x-axis and the y-axis. Perpendicular to each other, the axes divide the plane into four sections. Each section is called a quadrant; the quadrants are numbered counterclockwise as shown in the figure below.

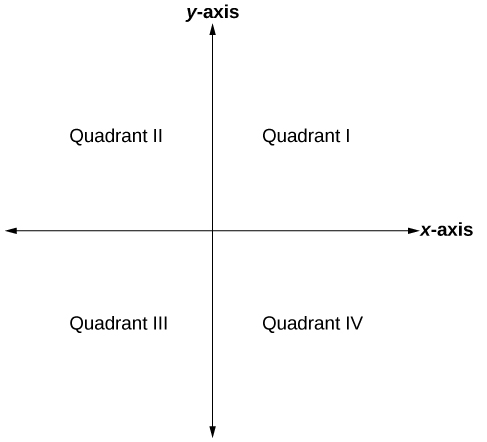
This is an image of an x, y plane with the axes labeled. The upper right section is labeled: Quadrant I. The upper left section is labeled: Quadrant II. The lower left section is labeled: Quadrant III. The lower right section is labeled: Quadrant IV.

The Cartesian coordinate system with all four quadrants labeled.

The center of the plane is the point at which the two axes cross. It is known as the origin or point [latex]\left(0,0\right)[/latex].

Each point in the plane is identified by its x-coordinate, or horizontal displacement from the origin, and its y-coordinate, or vertical displacement from the origin. Together we write them as an ordered pair indicating the combined distance from the origin in the form [latex]\left(x,y\right)[/latex]. An ordered pair is also known as a coordinate pair because it consists of x and y-coordinates. For example, we can represent the point [latex]\left(3,-1\right)[/latex] in the plane by moving three units to the right of the origin in the horizontal direction and one unit down in the vertical direction.

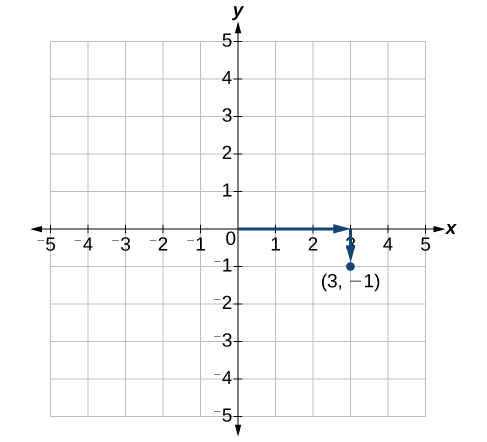
This is an image of an x, y coordinate plane. The x and y axis range from negative 5 to 5. The point (3, -1) is labeled. An arrow extends rightward from the origin 3 units and another arrow extends downward one unit from the end of that arrow to the point.

An illustration of how to plot the point (3,-1).

Cartesian Coordinate System

A two-dimensional plane where the

  • x-axis is the horizontal axis
  • y-axis is the vertical axis

A point in the plane is defined as an ordered pair, [latex]\left(x,y\right)[/latex], such that x is determined by its horizontal distance from the origin and y is determined by its vertical distance from the origin.

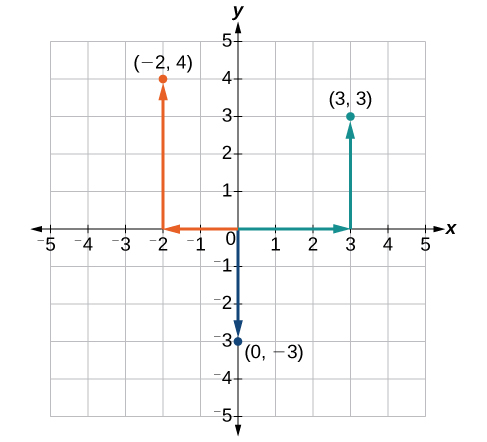
Example: Plotting Points in a Rectangular Coordinate System

Plot the points [latex]\left(-2,4\right)[/latex], [latex]\left(3,3\right)[/latex], and [latex]\left(0,-3\right)[/latex] in the coordinate plane.

Try It

Find Intercepts

The intercepts of a graph are points where the graph crosses the axes. The x-intercept is the point where the graph crosses the x-axis. At this point, the y-coordinate is zero. The y-intercept is the point where the graph crosses the y-axis. At this point, the x-coordinate is zero.

Regardless of the type of equation or function we are dealing with, to determine the x-intercept, we set y equal to zero and solve for x. Similarly, to determine the y-intercept, we set x equal to zero and solve for y. For example, lets find the intercepts of the equation [latex]y=3x - 1[/latex].

To find the x-intercept, set [latex]y=0[/latex].

[latex]\begin{array}{llllll}y=3x - 1\hfill & \hfill \\ 0=3x - 1\hfill & \hfill \\ 1=3x\hfill & \hfill \\ \frac{1}{3}=x\hfill & \hfill \\ \left(\frac{1}{3},0\right)\hfill & x\text{-intercept}\hfill \end{array}[/latex]

To find the y-intercept, set [latex]x=0[/latex].

[latex]\begin{array}{lllll}y=3x - 1\hfill & \hfill \\ y=3\left(0\right)-1\hfill & \hfill \\ y=-1\hfill & \hfill \\ \left(0,-1\right)\hfill & y\text{-intercept}\hfill \end{array}[/latex]

We can confirm that our results make sense by observing a graph of the equation. Notice that the graph crosses the axes where we predicted it would.

This is an image of a line graph on an x, y coordinate plane. The x and y-axis range from negative 4 to 4. The function y = 3x – 1 is plotted on the coordinate plane

Given an equation, find the intercepts

  1. Find the x-intercept by setting [latex]y=0[/latex] and solving for [latex]x[/latex].
  2. Find the y-intercept by setting [latex]x=0[/latex] and solving for [latex]y[/latex].

Example: Finding the Intercepts of the Given Equation

Find the intercepts of the equation [latex]y=-3x - 4[/latex]. Then sketch the graph using only the intercepts.

Try It

Find the intercepts of the equation and sketch the graph: [latex]y=-\frac{3}{4}x+3[/latex].

Square Binomials

When a binomial is squared, the result is called a perfect square trinomial. We can square a binomial by multiplying the binomial by itself. However, there is always a certain form that results from squaring a binomial. Memorizing the form makes squaring binomials much easier. Let’s look at a few binomials squared to familiarize ourselves with the form.

[latex]\begin{array}{ccc}\hfill \text{ }{\left(x+5\right)}^{2}& =& \text{ }{x}^{2}+10x+25\hfill \\ \hfill {\left(x - 3\right)}^{2}& =& \text{ }{x}^{2}-6x+9\hfill \\ \hfill {\left(4x - 1\right)}^{2}& =& 4{x}^{2}-8x+1\hfill \end{array}[/latex]

Notice that the first term of each trinomial is the square of the first term of the binomial and, similarly, the last term of each trinomial is the square of the last term of the binomial. The middle term is double the product of the two terms. Lastly, we see that the first sign of the trinomial is the same as the sign of the binomial.

Squaring a Binomial

When a binomial is squared, the result is the first term squared added to double the product of both terms and the last term squared.

[latex]{\left(x+a\right)}^{2}=\left(x+a\right)\left(x+a\right)={x}^{2}+2ax+{a}^{2}[/latex]

 

Given a binomial, square it using the Binomial Squaring Shortcut:

  1. Square the first term of the binomial.
  2. Square the last term of the binomial.
  3. For the middle term of the trinomial, double the product of the two terms.
  4. Add and simplify.

Example: Expanding Perfect Squares

Expand [latex]{\left(3x - 8\right)}^{2}[/latex].

Try It

Expand

a. [latex]{\left(4x - 1\right)}^{2}[/latex]

b. [latex]{\left(5y + 3\right)}^{2}[/latex]

c. [latex]{\left(w + 4z\right)}^{2}[/latex]

Try It