1. Derive the formula for the volume of a sphere using the slicing method.
2. Use the slicing method to derive the formula for the volume of a cone.
3. Use the slicing method to derive the formula for the volume of a tetrahedron with side length [latex]a.[/latex]
4. Use the disk method to derive the formula for the volume of a trapezoidal cylinder.
5. Explain when you would use the disk method versus the washer method. When are they interchangeable?
For the following exercises (6-10), draw a typical slice and find the volume using the slicing method for the given volume.
6. A pyramid with height 6 units and square base of side 2 units, as pictured here.

7. A pyramid with height 4 units and a rectangular base with length 2 units and width 3 units, as pictured here.

8. A tetrahedron with a base side of 4 units, as seen here.

9. A pyramid with height 5 units, and an isosceles triangular base with lengths of 6 units and 8 units, as seen here.

10. A cone of radius [latex]r[/latex] and height [latex]h[/latex] has a smaller cone of radius [latex]r\text{/}2[/latex] and height [latex]h\text{/}2[/latex] removed from the top, as seen here. The resulting solid is called a frustum.

For the following exercises (11-16), draw an outline of the solid and find the volume using the slicing method.
11. The base is a circle of radius [latex]a.[/latex] The slices perpendicular to the base are squares.
12. The base is a triangle with vertices [latex](0,0),(1,0),[/latex] and [latex](0,1).[/latex] Slices perpendicular to the xy-plane are semicircles.
13. The base is the region under the parabola [latex]y=1-{x}^{2}[/latex] in the first quadrant. Slices perpendicular to the xy-plane are squares.
14. The base is the region under the parabola [latex]y=1-{x}^{2}[/latex] and above the [latex]x\text{-axis}\text{.}[/latex] Slices perpendicular to the [latex]y\text{-axis}[/latex] are squares.
15. The base is the region enclosed by [latex]y={x}^{2}[/latex] and [latex]y=9.[/latex] Slices perpendicular to the [latex]x[/latex]-axis are right isosceles triangles.
16. The base is the area between [latex]y=x[/latex] and [latex]y={x}^{2}.[/latex] Slices perpendicular to the [latex]x[/latex]-axis are semicircles.
For the following exercises (17-24), draw the region bounded by the curves. Then, use the disk method to find the volume when the region is rotated around the [latex]x[/latex]-axis.
17. [latex]x+y=8,x=0,\text{ and }y=0[/latex]
18. [latex]y=2{x}^{2},x=0,x=4,\text{ and }y=0[/latex]
19. [latex]y={e}^{x}+1,x=0,x=1,\text{ and }y=0[/latex]
20. [latex]y={x}^{4},x=0,\text{ and }y=1[/latex]
21. [latex]y=\sqrt{x},x=0,x=4,\text{ and }y=0[/latex]
22. [latex]y= \sin x,y= \cos x,\text{ and }x=0[/latex]
23. [latex]y=\frac{1}{x},x=2,\text{ and }y=3[/latex]
24. [latex]{x}^{2}-{y}^{2}=9\text{ and }x+y=9,y=0\text{ and }x=0[/latex]
For the following exercises (25-32), draw the region bounded by the curves. Then, find the volume when the region is rotated around the [latex]y[/latex]-axis.
25. [latex]y=4-\frac{1}{2}x,x=0,\text{ and }y=0[/latex]
26. [latex]y=2{x}^{3},x=0,x=1,\text{ and }y=0[/latex]
27. [latex]y=3{x}^{2},x=0,\text{ and }y=3[/latex]
28. [latex]y=\sqrt{4-{x}^{2}},y=0,\text{ and }x=0[/latex]
29. [latex]y=\frac{1}{\sqrt{x+1}},x=0,\text{ and }x=3[/latex]
30. [latex]x= \sec (y)\text{ and }y=\frac{\pi }{4},y=0\text{ and }x=0[/latex]
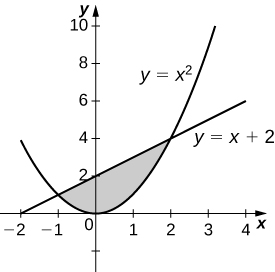
31. [latex]y=\frac{1}{x+1},x=0,\text{ and }x=2[/latex]
32. [latex]y=4-x,y=x,\text{ and }x=0[/latex]
For the following exercises (33-40), draw the region bounded by the curves. Then, find the volume when the region is rotated around the [latex]x[/latex]-axis.
33. [latex]y=x+2,y=x+6,x=0,\text{ and }x=5[/latex]
34. [latex]y={x}^{2}\text{ and }y=x+2[/latex]
35. [latex]{x}^{2}={y}^{3}\text{ and }{x}^{3}={y}^{2}[/latex]
36. [latex]y=4-{x}^{2}\text{ and }y=2-x[/latex]
37. [T] [latex]y= \cos x,y={e}^{\text{−}x},x=0,\text{ and }x=1.2927[/latex]
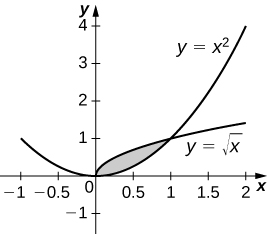
38. [latex]y=\sqrt{x}\text{ and }y={x}^{2}[/latex]
39. [latex]y= \sin x\text{,}y=5 \sin x,x=0\text{ and }x=\pi[/latex]
40. [latex]y=\sqrt{1+{x}^{2}}\text{ and }y=\sqrt{4-{x}^{2}}[/latex]
For the following exercises (41-45), draw the region bounded by the curves. Then, use the washer method to find the volume when the region is revolved around the [latex]y[/latex]-axis.
41. [latex]y=\sqrt{x},x=4,\text{ and }y=0[/latex]
42. [latex]y=x+2,y=2x-1,\text{ and }x=0[/latex]
43. [latex]y=\sqrt[3]{x}\text{ and }y={x}^{3}[/latex]
44. [latex]x={e}^{2y},x={y}^{2},y=0,\text{ and }y=\text{ln}(2)[/latex]
45. [latex]x=\sqrt{9-{y}^{2}},x={e}^{\text{−}y},y=0,\text{ and }y=3[/latex]
46. Yogurt containers can be shaped like frustums. Rotate the line [latex]y=\frac{1}{m}x[/latex] around the [latex]y[/latex]-axis to find the volume between [latex]y=a\text{ and }y=b.[/latex]

47. Rotate the ellipse [latex]({x}^{2}\text{/}{a}^{2})+({y}^{2}\text{/}{b}^{2})=1[/latex] around the [latex]x[/latex]-axis to approximate the volume of a football, as seen here.

48. Rotate the ellipse [latex]({x}^{2}\text{/}{a}^{2})+({y}^{2}\text{/}{b}^{2})=1[/latex] around the [latex]y[/latex]-axis to approximate the volume of a football.
49. A better approximation of the volume of a football is given by the solid that comes from rotating [latex]y= \sin x[/latex] around the [latex]x[/latex]-axis from [latex]x=0[/latex] to [latex]x=\pi .[/latex] What is the volume of this football approximation, as seen here?

50. What is the volume of the Bundt cake that comes from rotating [latex]y= \sin x[/latex] around the [latex]y[/latex]-axis from [latex]x=0[/latex] to [latex]x=\pi ?[/latex]

For the following exercises (51-56), find the volume of the solid described.
51. The base is the region between [latex]y=x[/latex] and [latex]y={x}^{2}.[/latex] Slices perpendicular to the [latex]x[/latex]-axis are semicircles.
52. The base is the region enclosed by the generic ellipse [latex]({x}^{2}\text{/}{a}^{2})+({y}^{2}\text{/}{b}^{2})=1.[/latex] Slices perpendicular to the [latex]x[/latex]-axis are semicircles.
53. Bore a hole of radius [latex]a[/latex] down the axis of a right cone and through the base of radius [latex]b,[/latex] as seen here.

54. Find the volume common to two spheres of radius [latex]r[/latex] with centers that are [latex]2h[/latex] apart, as shown here.

55. Find the volume of a spherical cap of height [latex]h[/latex] and radius [latex]r[/latex] where [latex]h
56. Find the volume of a sphere of radius [latex]R[/latex] with a cap of height [latex]h[/latex] removed from the top, as seen here.

Candela Citations
- Calculus Volume 1. Authored by: Gilbert Strang, Edwin (Jed) Herman. Provided by: OpenStax. Located at: https://openstax.org/details/books/calculus-volume-1. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike. License Terms: Access for free at https://openstax.org/books/calculus-volume-1/pages/1-introduction