Natural Logarithms

Learning Outcomes

  • Write the definition of the natural logarithm as an integral
  • Recognize the derivative of the natural logarithm
  • Integrate functions involving the natural logarithmic function
  • Define the number 𝑒 through an integral

The Natural Logarithm as an Integral

Recall the power rule for integrals:

[latex]\displaystyle\int {x}^{n}dx=\frac{{x}^{n+1}}{n+1}+C,n\ne \text{−}1.[/latex]

Clearly, this does not work when [latex]n=-1,[/latex] as it would force us to divide by zero. So, what do we do with [latex]\displaystyle\int \frac{1}{x}dx?[/latex] Recall from the Fundamental Theorem of Calculus that [latex]{\displaystyle\int }_{1}^{x}\dfrac{1}{t}dt[/latex] is an antiderivative of [latex]\frac{1}{x}.[/latex] Therefore, we can make the following definition.

Definition

For [latex]x>0,[/latex] define the natural logarithm function by

[latex]\text{ln}x={\displaystyle\int }_{1}^{x}\frac{1}{t}dt[/latex]

 

For [latex]x>1,[/latex] this is just the area under the curve [latex]y=1\text{/}t[/latex] from 1 to [latex]x.[/latex] For [latex]x<1,[/latex] we have [latex]{\displaystyle\int }_{1}^{x}\frac{1}{t}dt=\text{−}{\displaystyle\int }_{x}^{1}\frac{1}{t}dt,[/latex] so in this case it is the negative of the area under the curve from [latex]x\text{ to }1[/latex] (see the following figure).

 

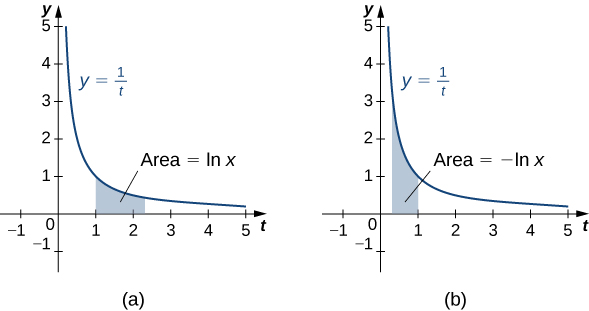
This figure has two graphs. The first is the curve y=1/t. It is decreasing and in the first quadrant. Under the curve is a shaded area. The area is bounded to the left at x=1. The area is labeled “area=lnx”. The second graph is the same curve y=1/t. It has shaded area under the curve bounded to the right by x=1. It is labeled “area=-lnx”.

Figure 1. (a) When [latex]x>1,[/latex] the natural logarithm is the area under the curve [latex]y=\frac{1}{t}[/latex] from [latex]1\text{ to }x.[/latex] (b) When [latex]x<1,[/latex] the natural logarithm is the negative of the area under the curve from [latex]x[/latex] to 1.

Notice that [latex]\text{ln}1=0.[/latex] Furthermore, the function [latex]y=\frac{1}{t}>0[/latex] for [latex]x>0.[/latex] Therefore, by the properties of integrals, it is clear that [latex]\text{ln}x[/latex] is increasing for [latex]x>0.[/latex]

Properties of the Natural Logarithm

Because of the way we defined the natural logarithm, the following differentiation formula falls out immediately as a result of to the Fundamental Theorem of Calculus.

Derivative of the Natural Logarithm

For [latex]x>0,[/latex] the derivative of the natural logarithm is given by

[latex]\frac{d}{dx}\text{ln}x=\dfrac{1}{x}.[/latex]

 

Corollary to the Derivative of the Natural Logarithm

The function [latex]\text{ln}x[/latex] is differentiable; therefore, it is continuous.

A graph of [latex]\text{ln}x[/latex] is shown in Figure 2. Notice that it is continuous throughout its domain of [latex](0,\infty ).[/latex]

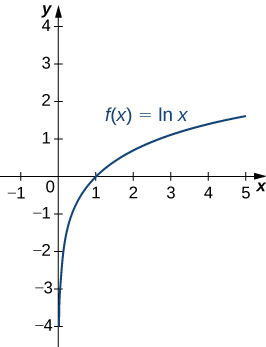
This figure is a graph. It is an increasing curve labeled f(x)=lnx. The curve is increasing with the y-axis as an asymptote. The curve intersects the x-axis at x=1.

Figure 2. The graph of [latex]f(x)=\text{ln}x[/latex] shows that it is a continuous function.

Example: Calculating Derivatives of Natural Logarithms

Calculate the following derivatives:

  1. [latex]\frac{d}{dx}\text{ln}(5{x}^{3}-2)[/latex]
  2. [latex]\frac{d}{dx}{(\text{ln}(3x))}^{2}[/latex]

Try It

Calculate the following derivatives:

  1. [latex]\frac{d}{dx}\text{ln}(2{x}^{2}+x)[/latex]
  2. [latex]\frac{d}{dx}{(\text{ln}({x}^{3}))}^{2}[/latex]

Watch the following video to see the worked solution to the above Try It.

Try It

Note that if we use the absolute value function and create a new function [latex]\text{ln}|x|,[/latex] we can extend the domain of the natural logarithm to include [latex]x<0.[/latex] Then [latex](d\text{/}(dx))\text{ln}|x|=1\text{/}x.[/latex] This gives rise to the familiar integration formula.

Integral of (1/[latex]u[/latex]) du

The natural logarithm is the antiderivative of the function [latex]f(u)=1\text{/}u\text{:}[/latex]

[latex]\displaystyle\int \frac{1}{u}du=\text{ln}|u|+C[/latex]

 

Example: Calculating Integrals Involving Natural Logarithms

Calculate the integral [latex]\displaystyle\int \frac{x}{{x}^{2}+4}dx.[/latex]

Try It

Calculate the integral [latex]\displaystyle\int \frac{{x}^{2}}{{x}^{3}+6}dx.[/latex]

Watch the following video to see the worked solution to the above Try It.

Try It

Although we have called our function a “logarithm,” we have not actually proved that any of the properties of logarithms hold for this function. We do so here.

Properties of the Natural Logarithm

If [latex]a,b>0[/latex] and [latex]r[/latex] is a rational number, then

  1. [latex]\text{ln}1=0[/latex]
  2. [latex]\text{ln}(ab)=\text{ln}a+\text{ln}b[/latex]
  3. [latex]\text{ln}(\frac{a}{b})=\text{ln}a-\text{ln}b[/latex]
  4. [latex]\text{ln}({a}^{r})=r\text{ln}a[/latex]

Proof

  1. By definition, [latex]\text{ln}1={\displaystyle\int }_{1}^{1}\frac{1}{t}dt=0.[/latex]
  2. We have
    [latex]\text{ln}(ab)={\displaystyle\int }_{1}^{ab}\frac{1}{t}dt={\displaystyle\int }_{1}^{a}\frac{1}{t}dt+{\displaystyle\int }_{a}^{ab}\frac{1}{t}dt.[/latex]

    Use [latex]u\text{-substitution}[/latex] on the last integral in this expression. Let [latex]u=t\text{/}a.[/latex] Then [latex]du=(1\text{/}a)dt.[/latex] Furthermore, when [latex]t=a,u=1,[/latex] and when [latex]t=ab,u=b.[/latex] So we get

    [latex]\text{ln}(ab)={\displaystyle\int }_{1}^{a}\frac{1}{t}dt+{\displaystyle\int }_{a}^{ab}\frac{1}{t}dt={\displaystyle\int }_{1}^{a}\frac{1}{t}dt+{\displaystyle\int }_{1}^{ab}\frac{a}{t}·\frac{1}{a}dt={\displaystyle\int }_{1}^{a}\frac{1}{t}dt+{\displaystyle\int }_{1}^{b}\frac{1}{u}du=\text{ln}a+\text{ln}b.[/latex]

     

  3. Note that
    [latex]\frac{d}{dx}\text{ln}({x}^{r})=\frac{r{x}^{r-1}}{{x}^{r}}=\frac{r}{x}.[/latex]

    Furthermore,

    [latex]\frac{d}{dx}(r\text{ln}x)=\frac{r}{x}.[/latex]

    Since the derivatives of these two functions are the same, by the Fundamental Theorem of Calculus, they must differ by a constant. So we have

    [latex]\text{ln}({x}^{r})=r\text{ln}x+C[/latex]

    for some constant [latex]C.[/latex] Taking [latex]x=1,[/latex] we get

    [latex]\begin{array}{ccc}\hfill \text{ln}({1}^{r})& =\hfill & r\text{ln}(1)+C\hfill \\ \hfill 0& =\hfill & r(0)+C\hfill \\ \hfill C& =\hfill & 0.\hfill \end{array}[/latex]

    Thus [latex]\text{ln}({x}^{r})=r\text{ln}x[/latex] and the proof is complete. Note that we can extend this property to irrational values of [latex]r[/latex] later in this section.
    Part iii. follows from parts ii. and iv. and the proof is left to you.

[latex]_\blacksquare[/latex]

Example: Using Properties of Logarithms

Use properties of logarithms to simplify the following expression into a single logarithm:

[latex]\text{ln}9-2\text{ln}3+\text{ln}(\frac{1}{3})[/latex] 

Try It

Use properties of logarithms to simplify the following expression into a single logarithm:

[latex]\text{ln}8-\text{ln}2-\text{ln}(\frac{1}{4}).[/latex]

Defining the Number [latex]e[/latex]

Now that we have the natural logarithm defined, we can use that function to define the number [latex]e.[/latex]

Definition

The number [latex]e[/latex] is defined to be the real number such that

[latex]\text{ln}e=1[/latex]

 

To put it another way, the area under the curve [latex]y=1\text{/}t[/latex] between [latex]t=1[/latex] and [latex]t=e[/latex] is 1 (Figure 3). The proof that such a number exists and is unique is left to you. (Hint: Use the Intermediate Value Theorem to prove existence and the fact that [latex]\text{ln}x[/latex] is increasing to prove uniqueness.)

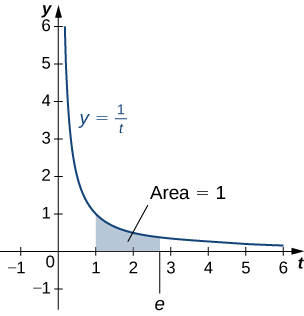
This figure is a graph. It is the curve y=1/t. It is decreasing and in the first quadrant. Under the curve is a shaded area. The area is bounded to the left at x=1 and to the right at x=e. The area is labeled “area=1”.

Figure 3. The area under the curve from 1 to [latex]e[/latex] is equal to one.

The number [latex]e[/latex] can be shown to be irrational, although we won’t do so here (see the activity in Taylor and Maclaurin Series in Calculus 2). Its approximate value is given by

[latex]e\approx 2.71828182846[/latex]