Skills Review for Basic Classes of Functions

Learning Outcomes

  • Evaluate a piecewise function
  • Identify important features of the graphs of “toolkit” functions

In Section 1.2, you will graph piecewise-defined functions and basic toolkit “parent” functions using transformations. To prepare you for graphing piecewise-defined functions, how to evaluate them is reviewed here. An introduction to basic toolkit “parent” functions is also provided here in order to reacquaint you with these functions so you can graph them using transformations.

Evaluate Piecewise-defined Functions

Sometimes, we come across a function that requires more than one formula in order to obtain the given output. A piecewise-defined function is a function in which more than one formula is used to define the output over different pieces of the domain.

We use piecewise functions to describe situations in which a rule or relationship changes as the input value crosses certain “boundaries.” For example, we often encounter situations in business for which the cost per piece of a certain item is discounted once the number ordered exceeds a certain value. Tax brackets are another real-world example of piecewise functions. For example, consider a simple tax system in which incomes up to [latex]$10,000[/latex] are taxed at [latex]10%[/latex], and any additional income is taxed at [latex]20\%[/latex]. The tax on a total income, [latex]S[/latex] , would be [latex]0.1S[/latex] if [latex]{S}\le$10,000[/latex]  and [latex]1000 + 0.2 (S - $10,000)[/latex] , if [latex]S> $10,000[/latex] .

A General Note: Piecewise-defined Functions

A piecewise-defined function is a function in which more than one formula is used to define the output. Each formula has its own domain, and the domain of the function is the union of all these smaller domains. We notate this idea like this:

[latex]f\left(x\right)=\begin{cases}\text{formula 1 if x is in domain 1}\\ \text{formula 2 if x is in domain 2}\\ \text{formula 3 if x is in domain 3}\end{cases}[/latex]

How To: Given a piecewise-Defined function, Evaluate it at a particular domain value

  1. Identify which piece of the function is defined at the given domain value.
  2. Plug the domain value into the piece where it is defined.
  3. Evaluate.

Example: Evaluating a Piecewise-Defined Function

A cell phone company uses the function below to determine the cost, [latex]C[/latex], in dollars for [latex]g[/latex] gigabytes of data transfer.

[latex]C\left(g\right)=\begin{cases}\begin{align}{25} \hspace{2mm}&\text{ if }\hspace{2mm}{ 0 }<{ g }<{ 2 }\\ { 25+10 }\left(g - 2\right) \hspace{2mm}&\text{ if }\hspace{2mm}{ g}\ge{ 2 }\end{align}\end{cases}[/latex]

Find the cost of using 1.5 gigabytes of data and the cost of using 4 gigabytes of data.

Try It

Try It

Identify Basic Toolkit “Parent” Functions

Below you will see information about basic toolkit “parent” functions, some of which will be useful in Section 1.2. It will be very helpful if we can recognize these toolkit functions and their features quickly by name, formula, graph, and basic table properties. The graphs and sample table values are included with each function shown below.

Toolkit Functions
Name Function Graph
Constant [latex]f\left(x\right)=c[/latex], where [latex]c[/latex] is a constant 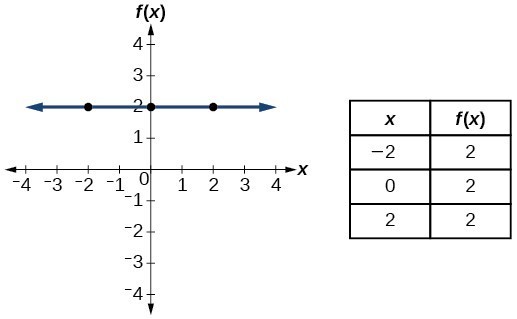Graph of a constant function.
Identity [latex]f\left(x\right)=x[/latex] Graph of a straight line.
Absolute value [latex]f\left(x\right)=|x|[/latex] 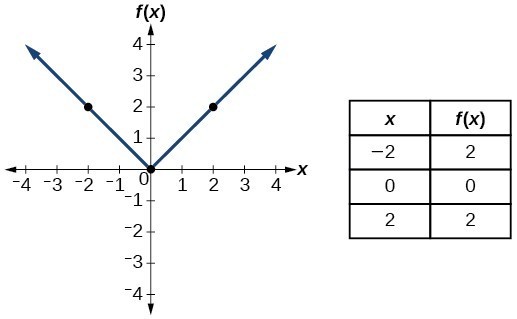Graph of absolute function.
Quadratic [latex]f\left(x\right)={x}^{2}[/latex] Graph of a parabola.
Cubic [latex]f\left(x\right)={x}^{3}[/latex] 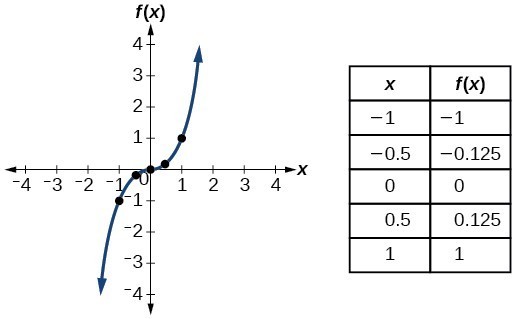Graph of f(x) = x^3.
Reciprocal/ Rational [latex]f\left(x\right)=\frac{1}{x}[/latex] 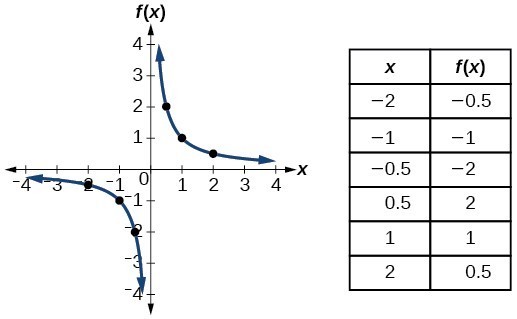Graph of f(x)=1/x.
Reciprocal / Rational squared [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex] 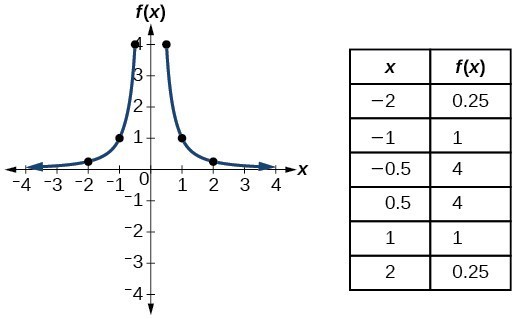Graph of f(x)=1/x^2.
Square root [latex]f\left(x\right)=\sqrt{x}[/latex] 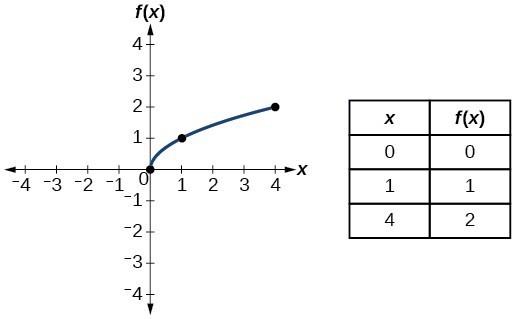Graph of f(x)=sqrt(x).
Cube root [latex]f\left(x\right)=\sqrt[3]{x}[/latex] 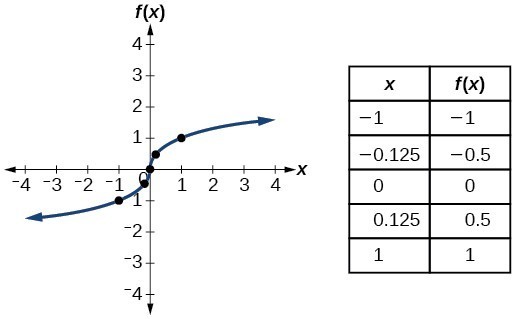Graph of f(x)=x^(1/3).

Try It