Learning Outcomes
- Identify reference angles for angles measured in both radians and degrees
- Evaluate trigonometric functions using the unit circle
- Use properties of even and odd trigonometric functions
In the Trigonometric Functions section, you will learn how to evaluate trigonometric functions at various angle measures and also graph trigonometric functions. Understanding how to find a reference angle of a given angle is an important skill needed to evaluate trigonometric functions and is reviewed here. Even-odd properties are also reviewed here, which will both help with evaluating trigonometric functions and graphing them.
Find Reference Angles
You will learn that it is easiest to evaluate trigonometric functions when an angle is in the first quadrant. When the original angle is given in quadrant two, three, or four, a reference angle should be found.
An angle’s reference angle is the acute angle, [latex]t[/latex], formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis. A reference angle is always an angle between [latex]0[/latex] and [latex]90^\circ[/latex], or [latex]0[/latex] and [latex]\frac{\pi }{2}[/latex] radians. As we can see in the figure below, for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.

A visual of the corresponding reference angles for each of the quadrants.
How To: Given an angle between [latex]0[/latex] and [latex]2\pi[/latex], find its reference angle.
- An angle in the first quadrant is its own reference angle.
- For an angle in the second or third quadrant, the reference angle is [latex]|\pi -t|[/latex] or [latex]|180^\circ \mathrm{-t}|[/latex].
- For an angle in the fourth quadrant, the reference angle is [latex]2\pi -t[/latex] or [latex]360^\circ \mathrm{-t}[/latex].
- If an angle is less than [latex]0[/latex] or greater than [latex]2\pi[/latex], add or subtract [latex]2\pi[/latex] as many times as needed to find an equivalent angle between [latex]0[/latex] and [latex]2\pi[/latex].
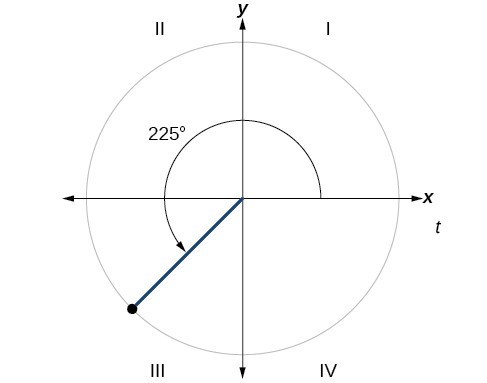
Example: Finding a Reference Angle
Find the reference angle of [latex]225^\circ[/latex] as shown in below.
Try It
Find the reference angle of [latex]\frac{5\pi }{3}[/latex].
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles. The quadrant of the original angle determines whether the answer is positive or negative. To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “A Smart Trig Class.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Smart,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Trig,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Class,” only cosine and its reciprocal function, secant, are positive.
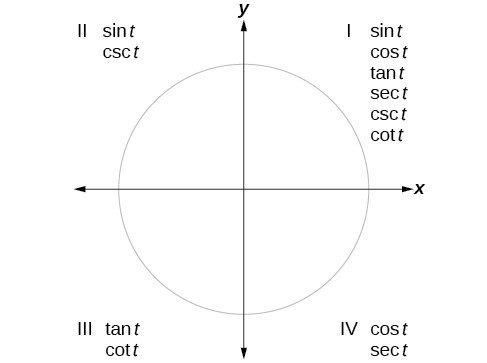
An illustration of which trigonometric functions are positive in each of the quadrants.
Evaluate Trigonometric Functions Using the Unit Circle
The unit circle tells us the value of cosine and sine at any of the given angle measures seen below. The first coordinate in each ordered pair is the value of cosine at the given angle measure, while the second coordinate in each ordered pair is the value of sine at the given angle measure. You will learn in Section 1.3 that all trigonometric functions can be written in terms of sine and cosine. Thus, if you can evaluate sine and cosine at various angle values, you can also evaluate the other trigonometric functions at various angle values. Take time to learn the [latex]\left(x,y\right)[/latex] coordinates of all of the major angles in the first quadrant of the unit circle.
Remember, every angle in quadrant two, three, or four has a reference angle that lies in quadrant one. The quadrant of the original angle only affects the sign (positive or negative) of a trigonometric function’s value at a given angle.
How To: Given the angle of a point on The Unit circle, find the Value of Cosine (Or Sine) using quadrant one.
- Find the reference angle using the appropriate reference angle formula from the first portion of this review section.
- Find the value of cosine (or sine) at the reference angle by looking at quadrant one of the unit circle.
- Determine the appropriate sign of your found value for cosine (or sine) based on the quadrant of the original angle.
Example: Using the Unit Circle to Find the Value of cosine
Use quadrant one of the unit circle to find the value of cosine at an angle of [latex]\frac{7\pi }{6}[/latex].
Try It
Use quadrant one of the unit circle to find the value of sine at an angle of [latex]\frac{5\pi }{3}[/latex].
Determine Even and Odd Trigonometric Functions
To be able to use our six trigonometric functions freely with both positive and negative angle inputs, we should examine how each function treats a negative input. As it turns out, there is an important difference among the functions in this regard.
Consider the function [latex]f\left(x\right)={x}^{2}[/latex], shown below. The graph of the function is symmetrical about the y-axis. All along the curve, any two points with opposite x-values have the same function value. This matches the result of calculation: [latex]{\left(4\right)}^{2}={\left(-4\right)}^{2}[/latex], [latex]{\left(-5\right)}^{2}={\left(5\right)}^{2}[/latex], and so on. So [latex]f\left(x\right)={x}^{2}[/latex] is an even function, a function such that two inputs that are opposites have the same output. That means [latex]f\left(-x\right)=f\left(x\right)[/latex].

The function [latex]f\left(x\right)={x}^{2}[/latex] is an even function.
Now consider the function [latex]f\left(x\right)={x}^{3}[/latex], shown below. The graph is not symmetrical about the y-axis. All along the graph, any two points with opposite x-values also have opposite y-values. So [latex]f\left(x\right)={x}^{3}[/latex] is an odd function, one such that two inputs that are opposites have outputs that are also opposites. That means [latex]f\left(-x\right)=-f\left(x\right)[/latex].

The function [latex]f\left(x\right)={x}^{3}[/latex] is an odd function.
A General Note: Even and Odd Trigonometric Functions
An even function is one in which [latex]f\left(-x\right)=f\left(x\right)[/latex].
An odd function is one in which [latex]f\left(-x\right)=-f\left(x\right)[/latex].
Cosine and secant are even:
[latex]\begin{gathered}\cos \left(-t\right)=\cos t \\ \sec \left(-t\right)=\sec t \end{gathered}[/latex]
Sine, tangent, cosecant, and cotangent are odd:
[latex]\begin{gathered}\sin \left(-t\right)=-\sin t \\ \tan \left(-t\right)=-\tan t \\ \csc \left(-t\right)=-\csc t \\ \cot \left(-t\right)=-\cot t \end{gathered}[/latex]
Example: Using Even and Odd Properties of Trigonometric Functions
If [latex]\sec t=2[/latex], what is the [latex]\sec (-t)[/latex]?
Try It
If [latex]\cot t=\sqrt{3}[/latex], what is [latex]\cot (-t)[/latex]?
Candela Citations
- Modification and Revision. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra Corequisite. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/waymakercollegealgebracorequisite/. License: CC BY: Attribution
- Precalculus. Provided by: Lumen Learning. Located at: https://courses.lumenlearning.com/precalculus/. License: CC BY: Attribution

