Applying L’Hôpital’s Rule

Learning Outcomes

Recognize when to apply L’Hôpital’s rule

Applying L’Hôpital’s Rule

L’Hôpital’s rule can be used to evaluate limits involving the quotient of two functions. Consider

lim_{x \to a} \frac{f (x)}{g (x)}

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}$

If $\underset{x\to a}{\lim}f(x)=L_1$ and $\underset{x\to a}{\lim}g(x)=L_2 \ne 0$ , then

lim_{x \to a} \frac{f (x)}{g (x)} = \frac{L_{1}}{L_{2}}

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}=\dfrac{L_1}{L_2}$

However, what happens if $\underset{x\to a}{\lim}f(x)=0$ and $\underset{x\to a}{\lim}g(x)=0$ ? We call this one of the indeterminate forms, of type $\frac{0}{0}$ . This is considered an indeterminate form because we cannot determine the exact behavior of $\frac{f(x)}{g(x)}$ as $x\to a$ without further analysis. We have seen examples of this earlier in the text. For example, consider

lim_{x \to 2} \frac{x^{2} - 4}{x - 2}

$\underset{x\to 2}{\lim}\dfrac{x^2-4}{x-2}$ and

lim_{x \to 0} \frac{\sin x}{x}

$\underset{x\to 0}{\lim}\dfrac{ \sin x}{x}$

For the first of these examples, we can evaluate the limit by factoring the numerator and writing

lim_{x \to 2} \frac{x^{2} - 4}{x - 2} = lim_{x \to 2} \frac{(x + 2) (x - 2)}{x - 2} = lim_{x \to 2} (x + 2) = 2 + 2 = 4

$\underset{x\to 2}{\lim}\dfrac{x^2-4}{x-2}=\underset{x\to 2}{\lim}\dfrac{(x+2)(x-2)}{x-2}=\underset{x\to 2}{\lim}(x+2)=2+2=4$

For $\underset{x\to 0}{\lim}\frac{\sin x}{x}$ we were able to show, using a geometric argument, that

lim_{x \to 0} \frac{\sin x}{x} = 1

$\underset{x\to 0}{\lim}\dfrac{\sin x}{x}=1$

Here we use a different technique for evaluating limits such as these. Not only does this technique provide an easier way to evaluate these limits, but also, and more important, it provides us with a way to evaluate many other limits that we could not calculate previously.

The idea behind L’Hôpital’s rule can be explained using local linear approximations. Consider two differentiable functions $f$ and $g$ such that $\underset{x\to a}{\lim}f(x)=0=\underset{x\to a}{\lim}g(x)$ and such that $g^{\prime}(a)\ne 0$ For $x$ near $a$ , we can write

f (x) \approx f (a) + f^{'} (a) (x - a)

$f(x)\approx f(a)+f^{\prime}(a)(x-a)$

and

g (x) \approx g (a) + g^{'} (a) (x - a)

$g(x)\approx g(a)+g^{\prime}(a)(x-a)$

Therefore,

\frac{f (x)}{g (x)} \approx \frac{f (a) + f^{'} (a) (x - a)}{g (a) + g^{'} (a) (x - a)}

$\dfrac{f(x)}{g(x)}\approx \dfrac{f(a)+f^{\prime}(a)(x-a)}{g(a)+g^{\prime}(a)(x-a)}$

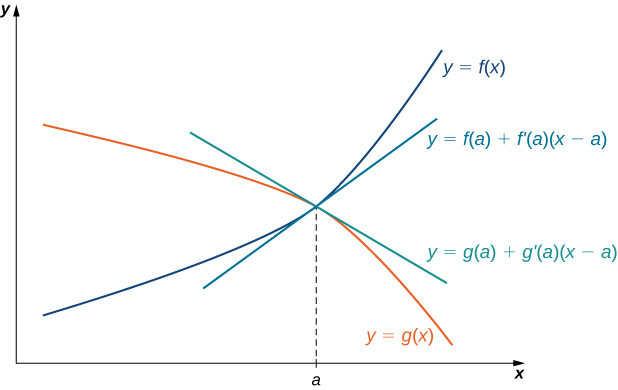
Two functions y = f(x) and y = g(x) are drawn such that they cross at a point above x = a. The linear approximations of these two functions y = f(a) + f’(a)(x – a) and y = g(a) + g’(a)(x – a) are also drawn.

Figure 1. If $\underset{x\to a}{\lim}f(x)=\underset{x\to a}{\lim}g(x)$ , then the ratio $f(x)/g(x)$ is approximately equal to the ratio of their linear approximations near $a$ .

Since $f$ is differentiable at $a$ , then $f$ is continuous at $a$ , and therefore $f(a)=\underset{x\to a}{\lim}f(x)=0$ . Similarly, $g(a)=\underset{x\to a}{\lim}g(x)=0$ . If we also assume that $f^{\prime}$ and $g^{\prime}$ are continuous at $x=a$ , then $f^{\prime}(a)=\underset{x\to a}{\lim}f^{\prime}(x)$ and $g^{\prime}(a)=\underset{x\to a}{\lim}g^{\prime}(x)$ . Using these ideas, we conclude that

lim_{x \to a} \frac{f (x)}{g (x)} = lim_{x \to a} \frac{f^{'} (x) (x - a)}{g^{'} (x) (x - a)} = lim_{x \to a} \frac{f^{'} (x)}{g^{'} (x)}

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}=\underset{x\to a}{\lim}\dfrac{f^{\prime}(x)(x-a)}{g^{\prime}(x)(x-a)}=\underset{x\to a}{\lim}\dfrac{f^{\prime}(x)}{g^{\prime}(x)}$

Note that the assumption that $f^{\prime}$ and $g^{\prime}$ are continuous at $a$ and $g^{\prime}(a)\ne 0$ can be loosened. We state L’Hôpital’s rule formally for the indeterminate form $\frac{0}{0}$ . Also note that the notation $\frac{0}{0}$ does not mean we are actually dividing zero by zero. Rather, we are using the notation $\frac{0}{0}$ to represent a quotient of limits, each of which is zero.

L’Hôpital’s Rule (0/0 Case)

Suppose $f$ and $g$ are differentiable functions over an open interval containing $a$ , except possibly at $a$ . If $\underset{x\to a}{\lim}f(x)=0$ and $\underset{x\to a}{\lim}g(x)=0$ , then

lim_{x \to a} \frac{f (x)}{g (x)} = lim_{x \to a} \frac{f^{'} (x)}{g^{'} (x)}

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}=\underset{x\to a}{\lim}\dfrac{f^{\prime}(x)}{g^{\prime}(x)}$ ,

assuming the limit on the right exists or is $\infty$ or $−\infty$ . This result also holds if we are considering one-sided limits, or if $a=\infty$ or $-\infty$ .

Proof

We provide a proof of this theorem in the special case when $f, \, g, \, f^{\prime}$ , and $g^{\prime}$ are all continuous over an open interval containing $a$ . In that case, since $\underset{x\to a}{\lim}f(x)=0=\underset{x\to a}{\lim}g(x)$ and $f$ and $g$ are continuous at $a$ , it follows that $f(a)=0=g(a)$ . Therefore,

\begin{array}{lllll} lim_{x \to a} \frac{f (x)}{g (x)} & = lim_{x \to a} \frac{f (x) - f (a)}{g (x) - g (a)} & since f (a) = 0 = g (a) \\ = lim_{x \to a} \frac{\frac{f (x) - f (a)}{x - a}}{\frac{g (x) - g (a)}{x - a}} & multiplying numerator and denominator by \frac{1}{x - a} \\ = \frac{lim_{x \to a} \frac{f (x) - f (a)}{x - a}}{lim_{x \to a} \frac{g (x) - g (a)}{x - a}} & limit of a quotient \\ = \frac{f^{'} (a)}{g^{'} (a)} & definition of the derivative \\ = \frac{lim_{x \to a} f^{'} (x)}{lim_{x \to a} g^{'} (x)} & continuity of f^{'} and g^{'} \\ = lim_{x \to a} \frac{f^{'} (x)}{g^{'} (x)} & limit of a quotient \end{array}

$\begin{array}{lllll} \underset{x\to a}{\lim}\frac{f(x)}{g(x)} & =\underset{x\to a}{\lim}\frac{f(x)-f(a)}{g(x)-g(a)} & & & \text{since} \, f(a)=0=g(a) \\ & =\underset{x\to a}{\lim}\frac{\frac{f(x)-f(a)}{x-a}}{\frac{g(x)-g(a)}{x-a}} & & & \text{multiplying numerator and denominator by} \, \frac{1}{x-a} \\ & =\frac{\underset{x\to a}{\lim}\frac{f(x)-f(a)}{x-a}}{\underset{x\to a}{\lim}\frac{g(x)-g(a)}{x-a}} & & & \text{limit of a quotient} \\ & =\frac{f^{\prime}(a)}{g^{\prime}(a)} & & & \text{definition of the derivative} \\ & =\frac{\underset{x\to a}{\lim}f^{\prime}(x)}{\underset{x\to a}{\lim}g^{\prime}(x)} & & & \text{continuity of} \, f^{\prime} \, \text{and} \, g^{\prime} \\ & =\underset{x\to a}{\lim}\frac{f^{\prime}(x)}{g^{\prime}(x)} & & & \text{limit of a quotient} \end{array}$

Note that L’Hôpital’s rule states we can calculate the limit of a quotient $\frac{f}{g}$ by considering the limit of the quotient of the derivatives $\frac{f^{\prime}}{g^{\prime}}$ . It is important to realize that we are not calculating the derivative of the quotient $\frac{f}{g}$ .

$_\blacksquare$

Example: Applying L’Hôpital’s Rule (0/0 Case)

Evaluate each of the following limits by applying L’Hôpital’s rule.

$\underset{x\to 0}{\lim}\dfrac{1- \cos x}{x}$
$\underset{x\to 1}{\lim}\dfrac{\sin (\pi x)}{\ln x}$
$\underset{x\to \infty }{\lim}\dfrac{e^{\frac{1}{x}}-1}{\frac{1}{x}}$
$\underset{x\to 0}{\lim}\dfrac{\sin x-x}{x^2}$

Show Solution

Since the numerator $1- \cos x\to 0$ and the denominator $x\to 0$ , we can apply L’Hôpital’s rule to evaluate this limit. We have
$\begin{array}{ll} \underset{x\to 0}{\lim}\frac{1- \cos x}{x} & =\underset{x\to 0}{\lim}\frac{\frac{d}{dx}(1- \cos x)}{\frac{d}{dx}(x)} \\ & =\underset{x\to 0}{\lim}\frac{\sin x}{1} \\ & =\frac{\underset{x\to 0}{\lim}(\sin x)}{\underset{x\to 0}{\lim}(1)} \\ & =\frac{0}{1}=0 \end{array}$
As $x\to 1$ , the numerator $\sin (\pi x)\to 0$ and the denominator $\ln x \to 0$ . Therefore, we can apply L’Hôpital’s rule. We obtain
$\begin{array}{ll} \underset{x\to 1}{\lim}\frac{\sin (\pi x)}{\ln x} & =\underset{x\to 1}{\lim}\frac{\pi \cos (\pi x)}{1/x} \\ & =\underset{x\to 1}{\lim}(\pi x) \cos (\pi x) \\ & =(\pi \cdot 1)(-1)=−\pi \end{array}$
As $x\to \infty$ , the numerator $e^{1/x}-1\to 0$ and the denominator $(\frac{1}{x})\to 0$ . Therefore, we can apply L’Hôpital’s rule. We obtain
$\underset{x\to \infty }{\lim}\frac{e^{1/x}-1}{\frac{1}{x}}=\underset{x\to \infty }{\lim}\frac{e^{1/x}(\frac{-1}{x^2})}{(\frac{-1}{x^2})}=\underset{x\to \infty}{\lim} e^{1/x}=e^0=1$
As $x\to 0$ , both the numerator and denominator approach zero. Therefore, we can apply L’Hôpital’s rule. We obtain
$\underset{x\to 0}{\lim}\frac{\sin x-x}{x^2}=\underset{x\to 0}{\lim}\frac{\cos x-1}{2x}$ .

Since the numerator and denominator of this new quotient both approach zero as $x\to 0$ , we apply L’Hôpital’s rule again. In doing so, we see that

$\underset{x\to 0}{\lim}\frac{\cos x-1}{2x}=\underset{x\to 0}{\lim}\frac{−\sin x}{2}=0$ .

Therefore, we conclude that

$\underset{x\to 0}{\lim}\frac{\sin x-x}{x^2}=0$ .

Watch the following video to see the worked solution to Example: Applying L’Hôpital’s Rule (0/0 Case).

Closed Captioning and Transcript Information for Video

Try It

Evaluate $\underset{x\to 0}{\lim}\dfrac{x}{\tan x}$ .

Hint

$\frac{d}{dx} \tan x= \sec ^2 x$

Show Solution

$1$

We can also use L’Hôpital’s rule to evaluate limits of quotients $\frac{f(x)}{g(x)}$ in which $f(x)\to \pm \infty$ and $g(x)\to \pm \infty$ . Limits of this form are classified as indeterminate forms of type $\infty / \infty$ . Again, note that we are not actually dividing $\infty$ by $\infty$ . Since $\infty$ is not a real number, that is impossible; rather, $\infty / \infty$ is used to represent a quotient of limits, each of which is $\infty$ or $−\infty$ .

L’Hôpital’s Rule ( $\infty / \infty$ Case)

Suppose $f$ and $g$ are differentiable functions over an open interval containing $a$ , except possibly at $a$ . Suppose $\underset{x\to a}{\lim}f(x)=\infty$ (or $−\infty$ ) and $\underset{x\to a}{\lim}g(x)=\infty$ (or $−\infty$ ). Then,

lim_{x \to a} \frac{f (x)}{g (x)} = lim_{x \to a} \frac{f^{'} (x)}{g^{'} (x)}

$\underset{x\to a}{\lim}\dfrac{f(x)}{g(x)}=\underset{x\to a}{\lim}\dfrac{f^{\prime}(x)}{g^{\prime}(x)}$ ,

assuming the limit on the right exists or is $\infty$ or $−\infty$ . This result also holds if the limit is infinite, if $a=\infty$ or $−\infty$ , or the limit is one-sided.

Example: Applying L’Hôpital’s Rule ( $\infty /\infty$ Case)

Evaluate each of the following limits by applying L’Hôpital’s rule.

$\underset{x\to \infty }{\lim}\dfrac{3x+5}{2x+1}$
$\underset{x\to 0^+}{\lim}\dfrac{\ln x}{\cot x}$

Show Solution

Since $3x+5$ and $2x+1$ are first-degree polynomials with positive leading coefficients, $\underset{x\to \infty }{\lim}(3x+5)=\infty$ and $\underset{x\to \infty }{\lim}(2x+1)=\infty$ . Therefore, we apply L’Hôpital’s rule and obtain
$\underset{x\to \infty}{\lim}\dfrac{3x+5}{2x+\frac{1}{x}}=\underset{x\to \infty }{\lim}\dfrac{3}{2}=\dfrac{3}{2}$ .

Note that this limit can also be calculated without invoking L’Hôpital’s rule. Earlier in the module we showed how to evaluate such a limit by dividing the numerator and denominator by the highest power of $x$ in the denominator. In doing so, we saw that

$\underset{x\to \infty }{\lim}\dfrac{3x+5}{2x+1}=\underset{x\to \infty }{\lim}\dfrac{3+\frac{5}{x}}{2+\frac{1}{x}}=\dfrac{3}{2}$ .

L’Hôpital’s rule provides us with an alternative means of evaluating this type of limit.
Here, $\underset{x\to 0^+}{\lim} \ln x=−\infty$ and $\underset{x\to 0^+}{\lim} \cot x=\infty$ . Therefore, we can apply L’Hôpital’s rule and obtain
$\underset{x\to 0^+}{\lim}\dfrac{\ln x}{\cot x}=\underset{x\to 0^+}{\lim}\dfrac{\frac{1}{x}}{−\csc^2 x}=\underset{x\to 0^+}{\lim}\dfrac{1}{−x \csc^2 x}$ .

Now as $x\to 0^+$ , $\csc^2 x\to \infty$ . Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In such a case, anything can happen with the product. Therefore, we cannot make any conclusion yet. To evaluate the limit, we use the definition of $\csc x$ to write

$\underset{x\to 0^+}{\lim}\dfrac{1}{−x \csc^2 x}=\underset{x\to 0^+}{\lim}\dfrac{\sin^2 x}{−x}$ .

Now $\underset{x\to 0^+}{\lim} \sin^2 x=0$ and $\underset{x\to 0^+}{\lim} x=0$ , so we apply L’Hôpital’s rule again. We find

$\underset{x\to 0^+}{\lim}\dfrac{\sin^2 x}{−x}=\underset{x\to 0^+}{\lim}\dfrac{2 \sin x \cos x}{-1}=\dfrac{0}{-1}=0$ .

We conclude that

$\underset{x\to 0^+}{\lim}\dfrac{\ln x}{\cot x}=0$ .

Try It

Evaluate $\underset{x\to \infty }{\lim}\dfrac{\ln x}{5x}$

Hint

$\frac{d}{dx}\ln x=\frac{1}{x}$

Show Solution

As mentioned, L’Hôpital’s rule is an extremely useful tool for evaluating limits. It is important to remember, however, that to apply L’Hôpital’s rule to a quotient $\frac{f(x)}{g(x)}$ , it is essential that the limit of $\frac{f(x)}{g(x)}$ be of the form $0/0$ or $\infty / \infty$ Consider the following example.

Example: When L’Hôpital’s Rule Does Not Apply

Consider $\underset{x\to 1}{\lim}\dfrac{x^2+5}{3x+4}$ . Show that the limit cannot be evaluated by applying L’Hôpital’s rule.

Show Solution

Because the limits of the numerator and denominator are not both zero and are not both infinite, we cannot apply L’Hôpital’s rule. If we try to do so, we get

\frac{d}{d x} (x^{2} + 5) = 2 x

$\frac{d}{dx}(x^2+5)=2x$

and

\frac{d}{d x} (3 x + 4) = 3

$\frac{d}{dx}(3x+4)=3$

At which point we would conclude erroneously that

lim_{x \to 1} \frac{x^{2} + 5}{3 x + 4} = lim_{x \to 1} \frac{2 x}{3} = \frac{2}{3}

$\underset{x\to 1}{\lim}\frac{x^2+5}{3x+4}=\underset{x\to 1}{\lim}\frac{2x}{3}=\frac{2}{3}$

However, since $\underset{x\to 1}{\lim}(x^2+5)=6$ and $\underset{x\to 1}{\lim}(3x+4)=7$ , we actually have

lim_{x \to 1} \frac{x^{2} + 5}{3 x + 4} = \frac{6}{7}

$\underset{x\to 1}{\lim}\frac{x^2+5}{3x+4}=\frac{6}{7}$

We can conclude that

lim_{x \to 1} \frac{x^{2} + 5}{3 x + 4} \neq lim_{x \to 1} \frac{\frac{d}{d x} (x^{2} + 5)}{\frac{d}{d x} (3 x + 4)}

$\underset{x\to 1}{\lim}\frac{x^2+5}{3x+4}\ne \underset{x\to 1}{\lim}\frac{\frac{d}{dx}(x^2+5)}{\frac{d}{dx}(3x+4)}$ .

Try It

Explain why we cannot apply L’Hôpital’s rule to evaluate $\underset{x\to 0^+}{\lim}\dfrac{\cos x}{x}$ . Evaluate $\underset{x\to 0^+}{\lim}\dfrac{\cos x}{x}$ by other means.

Hint

Show Solution

$\underset{x\to 0^+}{\lim} \cos x=1$ . Therefore, we cannot apply L’Hôpital’s rule. The limit of the quotient is $\infty$

Watch the following video to see the worked solution to the above Try It.

Closed Captioning and Transcript Information for Video

Module 4: Applications of Derivatives