Calculus of Hyperbolic and Inverse Hyperbolic Functions

Learning Outcomes

Apply the formulas for derivatives and integrals of the hyperbolic functions
Apply the formulas for the derivatives of the inverse hyperbolic functions and their associated integrals

Derivatives and Integrals of the Hyperbolic Functions

Recall that the hyperbolic sine and hyperbolic cosine are defined as

sinh x = \frac{e^{x} - e^{− x}}{2} and cosh x = \frac{e^{x} + e^{− x}}{2}

$\text{sinh}x=\dfrac{{e}^{x}-{e}^{\text{−}x}}{2}\text{ and }\text{cosh}x=\dfrac{{e}^{x}+{e}^{\text{−}x}}{2}$

The other hyperbolic functions are then defined in terms of $\text{sinh}x$ and $\text{cosh}x.$ The graphs of the hyperbolic functions are shown in the following figure.

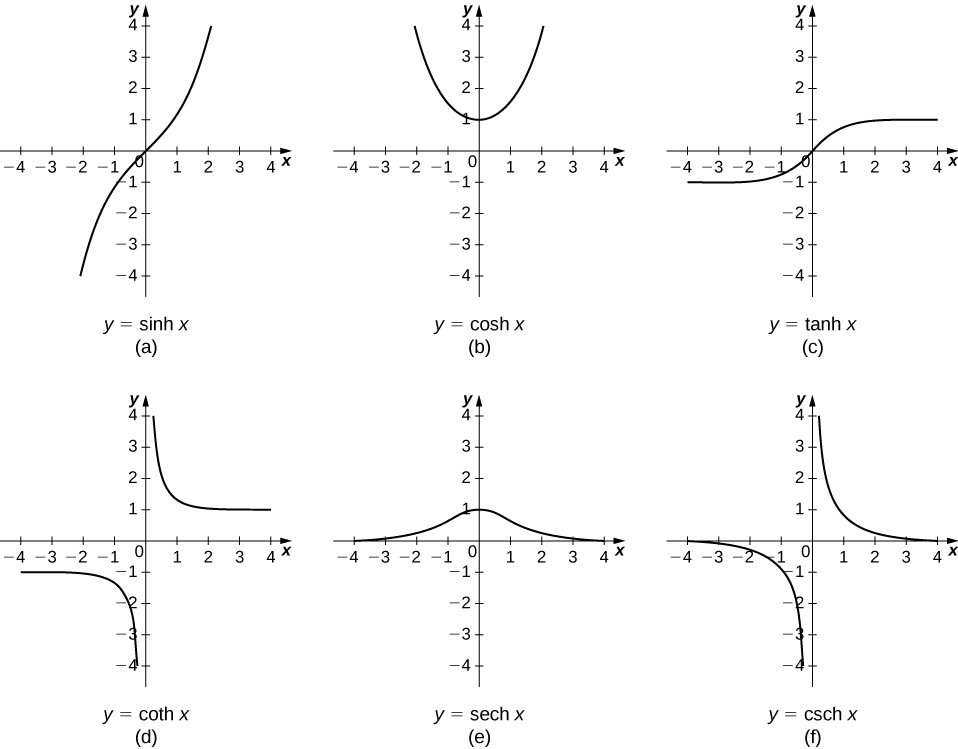
This figure has six graphs. The first graph labeled “a” is of the function y=sinh(x). It is an increasing function from the 3rd quadrant, through the origin to the first quadrant. The second graph is labeled “b” and is of the function y=cosh(x). It decreases in the second quadrant to the intercept y=1, then becomes an increasing function. The third graph labeled “c” is of the function y=tanh(x). It is an increasing function from the third quadrant, through the origin, to the first quadrant. The fourth graph is labeled “d” and is of the function y=coth(x). It has two pieces, one in the third quadrant and one in the first quadrant with a vertical asymptote at the y-axis. The fifth graph is labeled “e” and is of the function y=sech(x). It is a curve above the x-axis, increasing in the second quadrant, to the y-axis at y=1 and then decreases. The sixth graph is labeled “f” and is of the function y=csch(x). It has two pieces, one in the third quadrant and one in the first quadrant with a vertical asymptote at the y-axis.

Figure 1. Graphs of the hyperbolic functions.

It is easy to develop differentiation formulas for the hyperbolic functions. For example, looking at $\text{sinh}x$ we have

\begin{array}{cc} \frac{d}{d x} (sinh x) & = \frac{d}{d x} (\frac{e^{x} - e^{− x}}{2}) \\ = \frac{1}{2} [\frac{d}{d x} (e^{x}) - \frac{d}{d x} (e^{− x})] \\ = \frac{1}{2} [e^{x} + e^{− x}] = cosh x . \end{array}

$\begin{array}{cc}\hfill \frac{d}{dx}(\text{sinh}x)& =\frac{d}{dx}(\frac{{e}^{x}-{e}^{\text{−}x}}{2})\hfill \\ & =\frac{1}{2}\left[\frac{d}{dx}({e}^{x})-\frac{d}{dx}({e}^{\text{−}x})\right]\hfill \\ & =\frac{1}{2}\left[{e}^{x}+{e}^{\text{−}x}\right]=\text{cosh}x.\hfill \end{array}$

Similarly, $(\frac{d}{dx})\text{cosh}x=\text{sinh}x.$ We summarize the differentiation formulas for the hyperbolic functions in the following table.

Derivatives of the Hyperbolic Functions
$f(x)$	$\frac{d}{dx}f(x)$
$\text{sinh}x$	$\text{cosh}x$
$\text{cosh}x$	$\text{sinh}x$
$\text{tanh}x$	${\text{sech}}^{2}x$
$\text{coth}x$	$\text{−}{\text{csch}}^{2}x$
$\text{sech}x$	$\text{−}\text{sech}x\text{tanh}x$
$\text{csch}x$	$\text{−}\text{csch}x\text{coth}x$

Let’s take a moment to compare the derivatives of the hyperbolic functions with the derivatives of the standard trigonometric functions. There are a lot of similarities, but differences as well. For example, the derivatives of the sine functions match: $(\frac{d}{dx}) \sin x= \cos x$ and $(\frac{d}{dx})\text{sinh}x=\text{cosh}x.$ The derivatives of the cosine functions, however, differ in sign: $(\frac{d}{dx}) \cos x=\text{−} \sin x,$ but $(\frac{d}{dx})\text{cosh}x=\text{sinh}x.$ As we continue our examination of the hyperbolic functions, we must be mindful of their similarities and differences to the standard trigonometric functions.

These differentiation formulas for the hyperbolic functions lead directly to the following integral formulas.

\begin{array}{cccccccc} \int sinh u d u & = & cosh u + C & \int {csch}^{2} u d u & = & − coth u + C \\ \int cosh u d u & = & sinh u + C & \int sech u tanh u d u & = & − sech u + C \\ \int {sech}^{2} u d u & = & tanh u + C & \int csch u coth u d u & = & − csch u + C \end{array}

$\begin{array}{cccccccc}\hfill \displaystyle\int \text{sinh}udu& =\hfill & \text{cosh}u+C\hfill & & & \hfill \displaystyle\int {\text{csch}}^{2}udu& =\hfill & \text{−}\text{coth}u+C\hfill \\ \hfill \displaystyle\int \text{cosh}udu& =\hfill & \text{sinh}u+C\hfill & & & \hfill \displaystyle\int \text{sech}u\text{tanh}udu& =\hfill & \text{−}\text{sech}u+C\hfill \\ \hfill \displaystyle\int {\text{sech}}^{2}udu& =\hfill & \text{tanh}u+C\hfill & & & \hfill \displaystyle\int \text{csch}u\text{coth}udu& =\hfill & \text{−}\text{csch}u+C\hfill \end{array}$

Example: Differentiating Hyperbolic Functions

Evaluate the following derivatives:

$\frac{d}{dx}(\text{sinh}({x}^{2}))$
$\frac{d}{dx}{(\text{cosh}x)}^{2}$

Show Solution

Using the formulas in the table on derivatives of the hyperbolic functions and the chain rule, we get

$\frac{d}{dx}(\text{sinh}({x}^{2}))=\text{cosh}({x}^{2})·2x$
$\frac{d}{dx}{(\text{cosh}x)}^{2}=2\text{cosh}x\text{sinh}x$

Try It

Evaluate the following derivatives:

$\frac{d}{dx}(\text{tanh}({x}^{2}+3x))$
$\frac{d}{dx}(\dfrac{1}{{(\text{sinh}x)}^{2}})$

Show Solution

$\frac{d}{dx}(\text{tanh}({x}^{2}+3x))=({\text{sech}}^{2}({x}^{2}+3x))(2x+3)$
$\frac{d}{dx}(\frac{1}{{(\text{sinh}x)}^{2}})=\frac{d}{dx}{(\text{sinh}x)}^{-2}=-2{(\text{sinh}x)}^{-3}\text{cosh}x$

Hint

Use the formulas in the last example and apply the chain rule as necessary.

Watch the following video to see the worked solution to Example: Differentiating Hyperbolic Functions and the above Try It.

Closed Captioning and Transcript Information for Video

example: Integrals Involving Hyperbolic Functions

Evaluate the following integrals:

$\displaystyle\int x\text{cosh}({x}^{2})dx$
$\displaystyle\int \text{tanh}xdx$

Show Solution

We can use $u$ -substitution in both cases.

Let $u={x}^{2}.$ Then, $du=2xdx$ and
$\displaystyle\int x\text{cosh}({x}^{2})dx=\displaystyle\int \frac{1}{2}\text{cosh}udu=\frac{1}{2}\text{sinh}u+C=\frac{1}{2}\text{sinh}({x}^{2})+C.$
Let $u=\text{cosh}x.$ Then, $du=\text{sinh}xdx$ and
$\displaystyle\int \text{tanh}xdx=\displaystyle\int \frac{\text{sinh}x}{\text{cosh}x}dx=\displaystyle\int \frac{1}{u}du=\text{ln}|u|+C=\text{ln}|\text{cosh}x|+C.$

Note that $\text{cosh}x>0$ for all $x,$ so we can eliminate the absolute value signs and obtain

$\displaystyle\int \text{tanh}xdx=\text{ln}(\text{cosh}x)+C.$

Try It

Evaluate the following integrals:

$\displaystyle\int {\text{sinh}}^{3}x\text{cosh}xdx$
$\displaystyle\int {\text{sech}}^{2}(3x)dx$

Show Solution

$\displaystyle\int {\text{sinh}}^{3}x\text{cosh}xdx=\frac{{\text{sinh}}^{4}x}{4}+C$
$\displaystyle\int {\text{sech}}^{2}(3x)dx=\frac{\text{tanh}(3x)}{3}+C$

Hint

Use the formulas above and apply $u$ -substitution as necessary.

Watch the following video to see the worked solution to the above Try It.

Closed Captioning and Transcript Information for Video

Try It

Calculus of Inverse Hyperbolic Functions

Looking at the graphs of the hyperbolic functions, we see that with appropriate range restrictions, they all have inverses. Most of the necessary range restrictions can be discerned by close examination of the graphs. The domains and ranges of the inverse hyperbolic functions are summarized in the following table.

Domains and Ranges of the Inverse Hyperbolic Functions
Function	Domain	Range
${\text{sinh}}^{-1}x$	$(\text{−}\infty ,\infty )$	$(\text{−}\infty ,\infty )$
${\text{cosh}}^{-1}x$	$(1,\infty )$	$[0,\infty )$
${\text{tanh}}^{-1}x$	$(-1,1)$	$(\text{−}\infty ,\infty )$
${\text{coth}}^{-1}x$	$(\text{−}\infty ,-1)\cup (1,\infty )$	$(\text{−}\infty ,0)\cup (0,\infty )$
${\text{sech}}^{-1}x$	$(0\text{, 1})$	$[0,\infty )$
${\text{csch}}^{-1}x$	$(\text{−}\infty ,0)\cup (0,\infty )$	$(\text{−}\infty ,0)\cup (0,\infty )$

The graphs of the inverse hyperbolic functions are shown in the following figure.

This figure has six graphs. The first graph labeled “a” is of the function y=sinh^-1(x). It is an increasing function from the 3rd quadrant, through the origin to the first quadrant. The second graph is labeled “b” and is of the function y=cosh^-1(x). It is in the first quadrant, beginning on the x-axis at 2 and increasing. The third graph labeled “c” is of the function y=tanh^-1(x). It is an increasing function from the third quadrant, through the origin, to the first quadrant. The fourth graph is labeled “d” and is of the function y=coth^-1(x). It has two pieces, one in the third quadrant and one in the first quadrant with a vertical asymptote at the y-axis. The fifth graph is labeled “e” and is of the function y=sech^-1(x). It is a curve decreasing in the first quadrant and stopping on the x-axis at x=1. The sixth graph is labeled “f” and is of the function y=csch^-1(x). It has two pieces, one in the third quadrant and one in the first quadrant with a vertical asymptote at the y-axis.

Figure 2. Graphs of the inverse hyperbolic functions.

To find the derivatives of the inverse functions, we use implicit differentiation. We have

\begin{array}{ccc} y & = & {sinh}^{- 1} x \\ sinh y & = & x \\ \frac{d}{d x} sinh y & = & \frac{d}{d x} x \\ cosh y \frac{d y}{d x} & = & 1. \end{array}

$\begin{array}{ccc}\hfill y& =\hfill & {\text{sinh}}^{-1}x\hfill \\ \hfill \text{sinh}y& =\hfill & x\hfill \\ \hfill \frac{d}{dx}\text{sinh}y& =\hfill & \frac{d}{dx}x\hfill \\ \hfill \text{cosh}y\frac{dy}{dx}& =\hfill & 1.\hfill \end{array}$

Recall that ${\text{cosh}}^{2}y-{\text{sinh}}^{2}y=1,$ so $\text{cosh}y=\sqrt{1+{\text{sinh}}^{2}y}.$ Then,

\frac{d y}{d x} = \frac{1}{cosh y} = \frac{1}{\sqrt{1 + {sinh}^{2} y}} = \frac{1}{\sqrt{1 + x^{2}}} .

$\frac{dy}{dx}=\frac{1}{\text{cosh}y}=\frac{1}{\sqrt{1+{\text{sinh}}^{2}y}}=\frac{1}{\sqrt{1+{x}^{2}}}.$

We can derive differentiation formulas for the other inverse hyperbolic functions in a similar fashion. These differentiation formulas are summarized in the following table.

Derivatives of the Inverse Hyperbolic Functions
$f(x)$	$\frac{d}{dx}f(x)$
${\text{sinh}}^{-1}x$	$\frac{1}{\sqrt{1+{x}^{2}}}$
${\text{cosh}}^{-1}x$	$\frac{1}{\sqrt{{x}^{2}-1}}$
${\text{tanh}}^{-1}x$	$\frac{1}{1-{x}^{2}}$
${\text{coth}}^{-1}x$	$\frac{1}{1-{x}^{2}}$
${\text{sech}}^{-1}x$	$\frac{-1}{x\sqrt{1-{x}^{2}}}$
${\text{csch}}^{-1}x$	$\frac{-1}{\|x\|\sqrt{1+{x}^{2}}}$

Note that the derivatives of ${\text{tanh}}^{-1}x$ and ${\text{coth}}^{-1}x$ are the same. Thus, when we integrate $1\text{/}(1-{x}^{2}),$ we need to select the proper antiderivative based on the domain of the functions and the values of $x.$ Integration formulas involving the inverse hyperbolic functions are summarized as follows.

\begin{array}{cccccccc} \int \frac{1}{\sqrt{1 + u^{2}}} d u & = & {sinh}^{- 1} u + C & \int \frac{1}{u \sqrt{1 - u^{2}}} d u & = & − {sech}^{- 1} | u | + C \\ \int \frac{1}{\sqrt{u^{2} - 1}} d u & = & {cosh}^{- 1} u + C & \int \frac{1}{u \sqrt{1 + u^{2}}} d u & = & − {csch}^{- 1} | u | + C \\ \int \frac{1}{1 - u^{2}} d u & = & {\begin{matrix} {tanh}^{- 1} u + C if | u | < 1 \\ {coth}^{- 1} u + C if | u | > 1 \end{matrix} \end{array}

$\begin{array}{cccccccc}\hfill \displaystyle\int \frac{1}{\sqrt{1+{u}^{2}}}du& =\hfill & {\text{sinh}}^{-1}u+C\hfill & & & \hfill \displaystyle\int \frac{1}{u\sqrt{1-{u}^{2}}}du& =\hfill & \text{−}{\text{sech}}^{-1}|u|+C\hfill \\ \hfill \displaystyle\int \frac{1}{\sqrt{{u}^{2}-1}}du& =\hfill & {\text{cosh}}^{-1}u+C\hfill & & & \hfill \displaystyle\int \frac{1}{u\sqrt{1+{u}^{2}}}du& =\hfill & \text{−}{\text{csch}}^{-1}|u|+C\hfill \\ \hfill \displaystyle\int \frac{1}{1-{u}^{2}}du& =\hfill & \bigg\{\begin{array}{c}{\text{tanh}}^{-1}u+C\text{ if }|u|<1\hfill \\ {\text{coth}}^{-1}u+C\text{ if }|u|>1\hfill \end{array}\hfill & & & & & \end{array}$

Example: Differentiating Inverse Hyperbolic Functions

Evaluate the following derivatives:

$\frac{d}{dx}({\text{sinh}}^{-1}(\frac{x}{3}))$
$\frac{d}{dx}{({\text{tanh}}^{-1}x)}^{2}$

Show Solution

Using the formulas in the table on derivatives of the inverse hyperbolic functions and the chain rule, we obtain the following results:

$\frac{d}{dx}({\text{sinh}}^{-1}(\frac{x}{3}))=\frac{1}{3\sqrt{1+\frac{{x}^{2}}{9}}}=\frac{1}{\sqrt{9+{x}^{2}}}$
$\frac{d}{dx}{({\text{tanh}}^{-1}x)}^{2}=\frac{2({\text{tanh}}^{-1}x)}{1-{x}^{2}}$

Try It

Evaluate the following derivatives:

$\frac{d}{dx}({\text{cosh}}^{-1}(3x))$
$\frac{d}{dx}{({\text{coth}}^{-1}x)}^{3}$

Show Solution

$\frac{d}{dx}({\text{cosh}}^{-1}(3x))=\frac{3}{\sqrt{9{x}^{2}-1}}$
$\frac{d}{dx}{({\text{coth}}^{-1}x)}^{3}=\frac{3{({\text{coth}}^{-1}x)}^{2}}{1-{x}^{2}}$

Hint

Use the formulas in the table on derivatives of the inverse hyperbolic functions above and apply the chain rule as necessary.

Watch the following video to see the worked solution to the above Try It.

Closed Captioning and Transcript Information for Video

Example: Integrals Involving Inverse Hyperbolic Functions

Evaluate the following integrals:

$\displaystyle\int \frac{1}{\sqrt{4{x}^{2}-1}}dx$
$\displaystyle\int \frac{1}{2x\sqrt{1-9{x}^{2}}}dx$

Show Solution

We can use $u\text{-substitution}$ in both cases.

Let $u=2x.$ Then, $du=2dx$ and we have
$\displaystyle\int \frac{1}{\sqrt{4{x}^{2}-1}}dx=\displaystyle\int \frac{1}{2\sqrt{{u}^{2}-1}}du=\frac{1}{2}{\text{cosh}}^{-1}u+C=\frac{1}{2}{\text{cosh}}^{-1}(2x)+C.$
Let $u=3x.$ Then, $du=3dx$ and we obtain
$\displaystyle\int \frac{1}{2x\sqrt{1-9{x}^{2}}}dx=\frac{1}{2}\displaystyle\int \frac{1}{u\sqrt{1-{u}^{2}}}du=-\frac{1}{2}{\text{sech}}^{-1}|u|+C=-\frac{1}{2}{\text{sech}}^{-1}|3x|+C.$

Try It

Evaluate the following integrals:

$\displaystyle\int \frac{1}{\sqrt{{x}^{2}-4}}dx,\text{}x>2$
$\displaystyle\int \frac{1}{\sqrt{1-{e}^{2x}}}dx$

Show Solution

$\displaystyle\int \frac{1}{\sqrt{{x}^{2}-4}}dx={\text{cosh}}^{-1}(\frac{x}{2})+C$
$\displaystyle\int \frac{1}{\sqrt{1-{e}^{2x}}}dx=\text{−}{\text{sech}}^{-1}({e}^{x})+C$

Hint

Use the formulas above and apply $u\text{-substitution}$ as necessary.

Watch the following video to see the worked solution to the above Try It.

Closed Captioning and Transcript Information for Video

Module 6: Applications of Integration