Continuity at a Point

Learning Outcomes

  • Explain the three conditions for continuity at a point
  • Describe three kinds of discontinuities

We begin our investigation of continuity by exploring what it means for a function to have continuity at a point. Intuitively, a function is continuous at a particular point if there is no break in its graph at that point.

Before we look at a formal definition of what it means for a function to be continuous at a point, let’s consider various functions that fail to meet our intuitive notion of what it means to be continuous at a point. We then create a list of conditions that prevent such failures.

Our first function of interest is shown in Figure 1. We see that the graph of [latex]f(x)[/latex] has a hole at [latex]a[/latex]. In fact, [latex]f(a)[/latex] is undefined. At the very least, for [latex]f(x)[/latex] to be continuous at [latex]a[/latex], we need the following conditions:

i. [latex]f(a)[/latex] is defined.
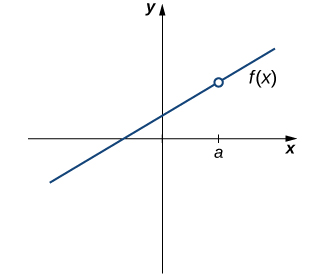
A graph of an increasing linear function f(x) which crosses the x axis from quadrant three to quadrant two and which crosses the y axis from quadrant two to quadrant one. A point a greater than zero is marked on the x axis. The point on the function f(x) above a is an open circle; the function is not defined at a.

Figure 1. The function [latex]f(x)[/latex] is not continuous at a because [latex]f(a)[/latex] is undefined.

However, as we see in Figure 2, this condition alone is insufficient to guarantee continuity at the point [latex]a[/latex]. Although [latex]f(a)[/latex] is defined, the function has a gap at [latex]a[/latex]. In this example, the gap exists because [latex]\underset{x\to a}{\lim}f(x)[/latex] does not exist. We must add another condition for continuity at [latex]a[/latex]—namely,

ii. [latex]\underset{x\to a}{\lim}f(x)[/latex] exists.
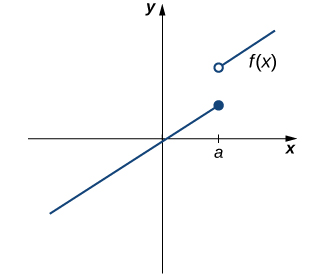
The graph of a piecewise function f(x) with two parts. The first part is an increasing linear function that crosses from quadrant three to quadrant one at the origin. A point a greater than zero is marked on the x axis. At fa. on this segment, there is a solid circle. The other segment is also an increasing linear function. It exists in quadrant one for values of x greater than a. At x=a, this segment has an open circle.

Figure 2. The function [latex]f(x)[/latex] is not continuous at a because [latex]\underset{x\to a}{\lim}f(x)[/latex] does not exist.

However, as we see in Figure 3, these two conditions by themselves do not guarantee continuity at a point. The function in this figure satisfies both of our first two conditions, but is still not continuous at [latex]a[/latex]. We must add a third condition to our list:

iii. [latex]\underset{x\to a}{\lim}f(x)=f(a)[/latex].
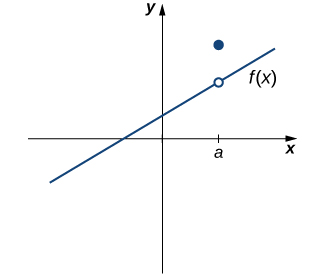
The graph of a piecewise function with two parts. The first part is an increasing linear function that crosses the x axis from quadrant three to quadrant two and which crosses the y axis from quadrant two to quadrant one. A point a greater than zero is marked on the x axis. At this point, there is an open circle on the linear function. The second part is a point at x=a above the line.

Figure 3. The function [latex]f(x)[/latex] is not continuous at a because [latex]\underset{x\to a}{\lim}f(x)\ne f(a)[/latex].

Now we put our list of conditions together and form a definition of continuity at a point.

Definition

A function [latex]f(x)[/latex] is continuous at a point [latex]a[/latex] if and only if the following three conditions are satisfied:

  1. [latex]f(a)[/latex] is defined
  2. [latex]\underset{x\to a}{\lim}f(x)[/latex] exists
  3. [latex]\underset{x\to a}{\lim}f(x)=f(a)[/latex]

A function is discontinuous at a point [latex]a[/latex] if it fails to be continuous at [latex]a[/latex].

The following procedure can be used to analyze the continuity of a function at a point using this definition.

Problem-Solving Strategy: Determining Continuity at a Point

  1. Check to see if [latex]f(a)[/latex] is defined. If [latex]f(a)[/latex] is undefined, we need go no further. The function is not continuous at [latex]a[/latex]. If [latex]f(a)[/latex] is defined, continue to step 2.
  2. Compute [latex]\underset{x\to a}{\lim}f(x)[/latex]. In some cases, we may need to do this by first computing [latex]\underset{x\to a^-}{\lim}f(x)[/latex] and [latex]\underset{x\to a^+}{\lim}f(x)[/latex]. If [latex]\underset{x\to a}{\lim}f(x)[/latex] does not exist (that is, it is not a real number), then the function is not continuous at [latex]a[/latex] and the problem is solved. If [latex]\underset{x\to a}{\lim}f(x)[/latex] exists, then continue to step 3.
  3. Compare [latex]f(a)[/latex] and [latex]\underset{x\to a}{\lim}f(x)[/latex]. If [latex]\underset{x\to a}{\lim}f(x)\ne f(a)[/latex], then the function is not continuous at [latex]a[/latex]. If [latex]\underset{x\to a}{\lim}f(x)=f(a)[/latex], then the function is continuous at [latex]a[/latex].

The next three examples demonstrate how to apply this definition to determine whether a function is continuous at a given point. These examples illustrate situations in which each of the conditions for continuity in the definition succeed or fail.

Example: Determining Continuity at a Point, Condition 1

Using the definition, determine whether the function [latex]f(x)=\dfrac{(x^2-4)}{(x-2)}[/latex] is continuous at [latex]x=2[/latex]. Justify the conclusion.

Example: Determining Continuity at a Point, Condition 2

Using the definition, determine whether the function [latex]f(x)=\begin{cases} -x^2+4 & \text{ if } \, x \le 3 \\ 4x-8 & \text{ if } \, x > 3 \end{cases}[/latex] is continuous at [latex]x=3[/latex]. Justify the conclusion.

Example: Determining Continuity at a Point, Condition 3

Using the definition, determine whether the function [latex]f(x)=\begin{cases} \frac{\sin x}{x} & \text{ if } \, x \ne 0 \\ 1 & \text{ if } \, x = 0 \end{cases}[/latex] is continuous at [latex]x=0[/latex].

Watch the following video to see the worked solution to the three Example: Determining Continuity at a Point conditions.

Try It

Using the definition, determine whether the function [latex]f(x)=\begin{cases} 2x+1 & \text{ if } \, x < 1 \\ 2 & \text{ if } \, x = 1 \\ -x+4 & \text{ if } \, x > 1 \end{cases}[/latex] is continuous at [latex]x=1[/latex]. If the function is not continuous at 1, indicate the condition for continuity at a point that fails to hold.

Try It

By applying the definition of continuity and previously established theorems concerning the evaluation of limits, we can state the following theorem.

Continuity of Polynomials and Rational Functions

Polynomials and rational functions are continuous at every point in their domains.

Proof

Previously, we showed that if [latex]p(x)[/latex] and [latex]q(x)[/latex] are polynomials, [latex]\underset{x\to a}{\lim}p(x)=p(a)[/latex] for every polynomial [latex]p(x)[/latex] and [latex]\underset{x\to a}{\lim}\dfrac{p(x)}{q(x)}=\dfrac{p(a)}{q(a)}[/latex] as long as [latex]q(a)\ne 0[/latex]. Therefore, polynomials and rational functions are continuous on their domains.

[latex]_\blacksquare[/latex]

Recall: Domain of polynomial and rational functions

The domain of every polynomial function is all real numbers. 

The domain of a rational functional can be found by:

  1. Set the denominator equal to zero.
  2. Solve to find the values of the variable that cause the denominator to equal zero.
  3. The domain contains all real numbers except those found in Step 2.

We now apply continuity of polynomials and rational functions to determine the points at which a given rational function is continuous.

Example: Continuity of a Rational Function

For what values of [latex]x[/latex] is [latex]f(x)=\dfrac{x+1}{x-5}[/latex] continuous?

Try It

For what values of [latex]x[/latex] is [latex]f(x)=3x^4-4x^2[/latex] continuous?

Types of Discontinuities

As we have seen in the earlier examples, discontinuities take on several different appearances. We classify the types of discontinuities we have seen thus far as removable discontinuities, infinite discontinuities, or jump discontinuities. Intuitively, a removable discontinuity is a discontinuity for which there is a hole in the graph, a jump discontinuity is a noninfinite discontinuity for which the sections of the function do not meet up, and an infinite discontinuity is a discontinuity located at a vertical asymptote. Figure 6 illustrates the differences in these types of discontinuities. Although these terms provide a handy way of describing three common types of discontinuities, keep in mind that not all discontinuities fit neatly into these categories.

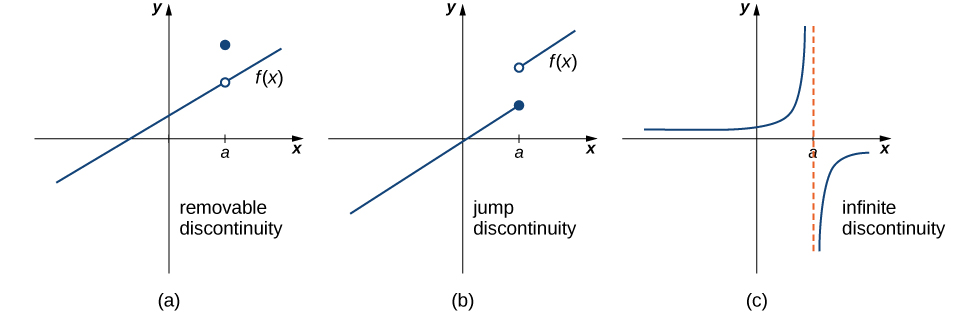
"Three 0, there is an open circle on the line and a closed circle a few units above the line. The second is a jump discontinuity. Here, there are two lines with positive slope. The first line exists for x<=a, and the second exists for x>a, where a>0. The first line ends at a solid circle where x=a, and the second begins a few units up with an open circle at x=a. The third discontinuity type is infinite discontinuity. Here, the function has two parts separated by an asymptote x=a. The first segment is a curve stretching along the x axis to 0 as x goes to negative infinity and along the y axis to infinity as x goes to zero. The second segment is a curve stretching along the y axis to negative infinity as x goes to zero and along the x axis to 0 as x goes to infinity." width="975" height="315"

Figure 6. Discontinuities are classified as (a) removable, (b) jump, or (c) infinite.

These three discontinuities are formally defined as follows:

Definition

If [latex]f(x)[/latex] is discontinuous at [latex]a[/latex], then

  1. [latex]f[/latex] has a removable discontinuity at [latex]a[/latex] if [latex]\underset{x\to a}{\lim}f(x)[/latex] exists. (Note: When we state that [latex]\underset{x\to a}{\lim}f(x)[/latex] exists, we mean that [latex]\underset{x\to a}{\lim}f(x)=L[/latex], where [latex]L[/latex] is a real number.)
  2. [latex]f[/latex] has a jump discontinuity at [latex]a[/latex] if [latex]\underset{x\to a^-}{\lim}f(x)[/latex] and [latex]\underset{x\to a^+}{\lim}f(x)[/latex] both exist, but [latex]\underset{x\to a^-}{\lim}f(x)\ne \underset{x\to a^+}{\lim}f(x)[/latex]. (Note: When we state that [latex]\underset{x\to a^-}{\lim}f(x)[/latex] and [latex]\underset{x\to a^+}{\lim}f(x)[/latex] both exist, we mean that both are real-valued and that neither take on the values [latex]\pm \infty[/latex].)
  3. [latex]f[/latex] has an infinite discontinuity at [latex]a[/latex] if [latex]\underset{x\to a^-}{\lim}f(x)=\pm \infty [/latex] or [latex]\underset{x\to a^+}{\lim}f(x)=\pm \infty[/latex].

Example: Classifying a Discontinuity 1

In an earlier example, we showed that [latex]f(x)=\dfrac{x^2-4}{x-2}[/latex] is discontinuous at [latex]x=2[/latex]. Classify this discontinuity as removable, jump, or infinite.

Example: Classifying a Discontinuity 2

In an earlier example, we showed that [latex]f(x)=\begin{cases} -x^2+4 & \text{ if } \, x \le 3 \\ 4x-8 & \text{ if } \, x > 3 \end{cases}[/latex] is discontinuous at [latex]x=3[/latex]. Classify this discontinuity as removable, jump, or infinite.

Example: Classifying a Discontinuity 3

Determine whether [latex]f(x)=\dfrac{x+2}{x+1}[/latex] is continuous at −1. If the function is discontinuous at −1, classify the discontinuity as removable, jump, or infinite.

Watch the following video to see the worked solution to the three Example: Classifying a Discontinuity conditions.

Try It

For [latex]f(x)=\begin{cases} x^2 & \text{ if } \, x \ne 1 \\ 3 & \text{ if } \, x = 1 \end{cases}[/latex], decide whether [latex]f[/latex] is continuous at 1. If [latex]f[/latex] is not continuous at 1, classify the discontinuity as removable, jump, or infinite.