Again, we are working with a solid of revolution. As before, we define a region [latex]R,[/latex] bounded above by the graph of a function [latex]y=f(x),[/latex] below by the [latex]x\text{-axis,}[/latex] and on the left and right by the lines [latex]x=a[/latex] and [latex]x=b,[/latex] respectively, as shown in Figure 1(a). We then revolve this region around the [latex]y[/latex]-axis, as shown in Figure 1(b). Note that this is different from what we have done before. Previously, regions defined in terms of functions of [latex]x[/latex] were revolved around the [latex]x\text{-axis}[/latex] or a line parallel to it.

Figure 1. (a) A region bounded by the graph of a function of [latex]x.[/latex] (b) The solid of revolution formed when the region is revolved around the [latex]y\text{-axis}\text{.}[/latex]

As we have done many times before, partition the interval [latex]\left[a,b\right][/latex] using a regular partition, [latex]P=\left\{{x}_{0},{x}_{1}\text{,…},{x}_{n}\right\}[/latex] and, for [latex]i=1,2\text{,…},n,[/latex] choose a point [latex]{x}_{i}^{*}\in \left[{x}_{i-1},{x}_{i}\right].[/latex] Then, construct a rectangle over the interval [latex]\left[{x}_{i-1},{x}_{i}\right][/latex] of height [latex]f({x}_{i}^{*})[/latex] and width [latex]\text{Δ}x.[/latex] A representative rectangle is shown in Figure 2(a). When that rectangle is revolved around the [latex]y[/latex]-axis, instead of a disk or a washer, we get a cylindrical shell, as shown in the following figure.

Figure 2. (a) A representative rectangle. (b) When this rectangle is revolved around the [latex]y\text{-axis},[/latex] the result is a cylindrical shell. (c) When we put all the shells together, we get an approximation of the original solid.

To calculate the volume of this shell, consider Figure 3.

Figure 3. Calculating the volume of the shell.

Notice that the rectangle we are using is parallel to the axis of revolution (y axis), not perpendicular like the disk and washer method. This could be very useful, particularly for y axis revolutions.

The shell is a cylinder, so its volume is the cross-sectional area multiplied by the height of the cylinder. The cross-sections are annuli (ring-shaped regions—essentially, circles with a hole in the center), with outer radius [latex]{x}_{i}[/latex] and inner radius [latex]{x}_{i-1}.[/latex] Thus, the cross-sectional area is [latex]\pi {x}_{i}^{2}-\pi {x}_{i-1}^{2}.[/latex] The height of the cylinder is [latex]f({x}_{i}^{*}).[/latex] Then the volume of the shell is

Note that [latex]{x}_{i}-{x}_{i-1}=\text{Δ}x,[/latex] so we have

Furthermore, [latex]\frac{{x}_{i}+{x}_{i-1}}{2}[/latex] is both the midpoint of the interval [latex]\left[{x}_{i-1},{x}_{i}\right][/latex] and the average radius of the shell, and we can approximate this by [latex]{x}_{i}^{*}.[/latex] We then have

Another way to think of this is to think of making a vertical cut in the shell and then opening it up to form a flat plate (Figure 4).

Figure 4. (a) Make a vertical cut in a representative shell. (b) Open the shell up to form a flat plate.

In reality, the outer radius of the shell is greater than the inner radius, and hence the back edge of the plate would be slightly longer than the front edge of the plate. However, we can approximate the flattened shell by a flat plate of height [latex]f({x}_{i}^{*}),[/latex] width [latex]2\pi {x}_{i}^{*},[/latex] and thickness [latex]\text{Δ}x[/latex] (Figure 4). The volume of the shell, then, is approximately the volume of the flat plate. Multiplying the height, width, and depth of the plate, we get

which is the same formula we had before.

To calculate the volume of the entire solid, we then add the volumes of all the shells and obtain

Here we have another Riemann sum, this time for the function [latex]2\pi xf(x).[/latex] Taking the limit as [latex]n\to \infty[/latex] gives us

This leads to the following rule for the method of cylindrical shells.

Now let’s consider an example.

Example: The Method of Cylindrical Shells 1

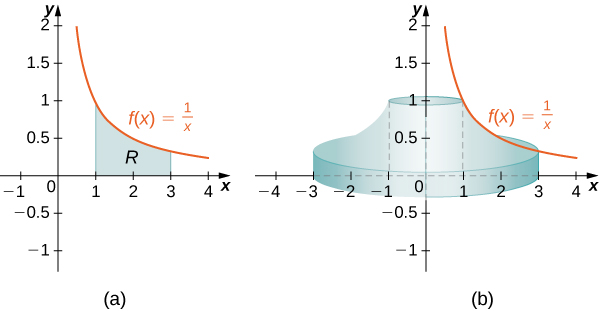
Define [latex]R[/latex] as the region bounded above by the graph of [latex]f(x)=1\text{/}x[/latex] and below by the [latex]x\text{-axis}[/latex] over the interval [latex]\left[1,3\right].[/latex] Find the volume of the solid of revolution formed by revolving [latex]R[/latex] around the [latex]y\text{-axis}.[/latex]

Show Solution

First we must graph the region [latex]R[/latex] and the associated solid of revolution, as shown in the following figure.

Figure 5. (a) The region [latex]R[/latex] under the graph of [latex]f(x)=1\text{/}x[/latex] over the interval [latex]\left[1,3\right].[/latex] (b) The solid of revolution generated by revolving [latex]R[/latex] about the [latex]y\text{-axis}.[/latex]

Then the volume of the solid is given by

[latex]\begin{array}{cc}\hfill V& ={\displaystyle\int }_{a}^{b}(2\pi xf(x))dx\hfill \\ & ={\displaystyle\int }_{1}^{3}(2\pi x(\frac{1}{x}))dx\hfill \\ & ={\displaystyle\int }_{1}^{3}2\pi dx={2\pi x|}_{1}^{3}=4\pi {\text{units}}^{3}\text{.}\hfill \end{array}[/latex]

example: The Method of Cylindrical Shells 2

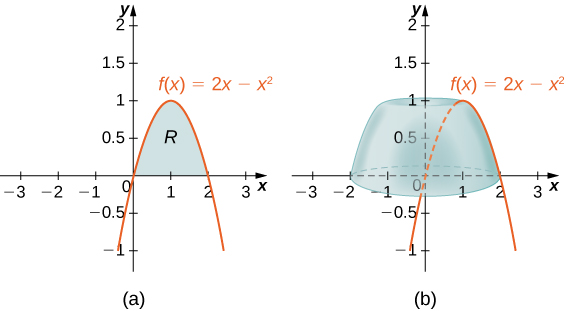
Define [latex]R[/latex] as the region bounded above by the graph of [latex]f(x)=2x-{x}^{2}[/latex] and below by the [latex]x\text{-axis}[/latex] over the interval [latex]\left[0,2\right].[/latex] Find the volume of the solid of revolution formed by revolving [latex]R[/latex] around the [latex]y\text{-axis}.[/latex]

Show Solution

First graph the region [latex]R[/latex] and the associated solid of revolution, as shown in the following figure.

Figure 6. (a) The region [latex]R[/latex] under the graph of [latex]f(x)=2x-{x}^{2}[/latex] over the interval [latex]\left[0,2\right].[/latex] (b) The volume of revolution obtained by revolving [latex]R[/latex] about the [latex]y\text{-axis}.[/latex]

Then the volume of the solid is given by

[latex]\begin{array}{cc}\hfill V& ={\displaystyle\int }_{a}^{b}(2\pi xf(x))dx\hfill \\ & ={\displaystyle\int }_{0}^{2}(2\pi x(2x-{x}^{2}))dx=2\pi {\displaystyle\int }_{0}^{2}(2{x}^{2}-{x}^{3})dx\hfill \\ & ={2\pi \left[\frac{2{x}^{3}}{3}-\frac{{x}^{4}}{4}\right]|}_{0}^{2}=\frac{8\pi }{3}{\text{units}}^{3}\text{.}\hfill \end{array}[/latex]

As with the disk method and the washer method, we can use the method of cylindrical shells with solids of revolution, revolved around the [latex]x\text{-axis},[/latex] when we want to integrate with respect to [latex]y.[/latex] The analogous rule for this type of solid is given here.

example: The Method of Cylindrical Shells for a Solid Revolved around the [latex]x[/latex]-axis

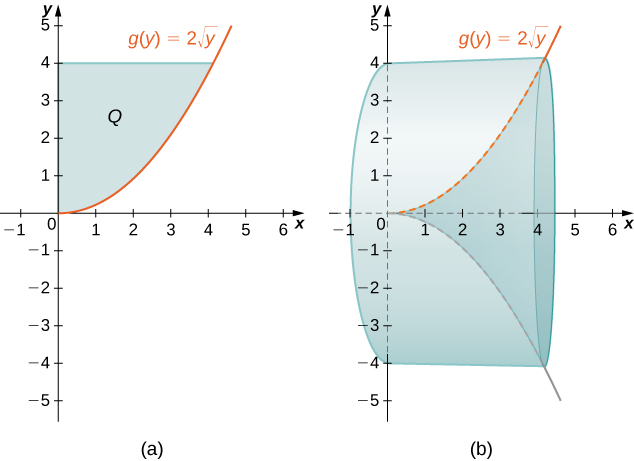
Define [latex]Q[/latex] as the region bounded on the right by the graph of [latex]g(y)=2\sqrt{y}[/latex] and on the left by the [latex]y\text{-axis}[/latex] for [latex]y\in \left[0,4\right].[/latex] Find the volume of the solid of revolution formed by revolving [latex]Q[/latex] around the [latex]x[/latex]-axis.

Show Solution

First, we need to graph the region [latex]Q[/latex] and the associated solid of revolution, as shown in the following figure.

Figure 7. (a) The region [latex]Q[/latex] to the left of the function [latex]g(y)[/latex] over the interval [latex]\left[0,4\right].[/latex] (b) The solid of revolution generated by revolving [latex]Q[/latex] around the [latex]x\text{-axis}.[/latex]

Label the shaded region [latex]Q.[/latex] Then the volume of the solid is given by

[latex]\begin{array}{cc}\hfill V& ={\displaystyle\int }_{c}^{d}(2\pi yg(y))dy\hfill \\ & ={\displaystyle\int }_{0}^{4}(2\pi y(2\sqrt{y}))dy=4\pi {\displaystyle\int }_{0}^{4}{y}^{3\text{/}2}dy\hfill \\ & ={4\pi \left[\frac{2{y}^{5\text{/}2}}{5}\right]|}_{0}^{4}=\frac{256\pi }{5}{\text{units}}^{3}\text{.}\hfill \end{array}[/latex]

Watch the following video to see the worked solution to the above Try It.

For the next example, we look at a solid of revolution for which the graph of a function is revolved around a line other than one of the two coordinate axes. To set this up, we need to revisit the development of the method of cylindrical shells. Recall that we found the volume of one of the shells to be given by

This was based on a shell with an outer radius of [latex]{x}_{i}[/latex] and an inner radius of [latex]{x}_{i-1}.[/latex] If, however, we rotate the region around a line other than the [latex]y\text{-axis},[/latex] we have a different outer and inner radius. Suppose, for example, that we rotate the region around the line [latex]x=\text{−}k,[/latex] where [latex]k[/latex] is some positive constant. Then, the outer radius of the shell is [latex]{x}_{i}+k[/latex] and the inner radius of the shell is [latex]{x}_{i-1}+k.[/latex] Substituting these terms into the expression for volume, we see that when a plane region is rotated around the line [latex]x=\text{−}k,[/latex] the volume of a shell is given by

As before, we notice that [latex]\frac{{x}_{i}+{x}_{i-1}}{2}[/latex] is the midpoint of the interval [latex]\left[{x}_{i-1},{x}_{i}\right][/latex] and can be approximated by [latex]{x}_{i}^{*}.[/latex] Then, the approximate volume of the shell is

The remainder of the development proceeds as before, and we see that

We could also rotate the region around other horizontal or vertical lines, such as a vertical line in the right half plane. In each case, the volume formula must be adjusted accordingly. Specifically, the [latex]x\text{-term}[/latex] in the integral must be replaced with an expression representing the radius of a shell. To see how this works, consider the following example.

Example: A Region of Revolution Revolved around a Line

Define [latex]R[/latex] as the region bounded above by the graph of [latex]f(x)=x[/latex] and below by the [latex]x\text{-axis}[/latex] over the interval [latex]\left[1,2\right].[/latex] Find the volume of the solid of revolution formed by revolving [latex]R[/latex] around the line [latex]x=-1.[/latex]

Show Solution

First, graph the region [latex]R[/latex] and the associated solid of revolution, as shown in the following figure.

Figure 8. (a) The region [latex]R[/latex] between the graph of [latex]f(x)[/latex] and the [latex]x\text{-axis}[/latex] over the interval [latex]\left[1,2\right].[/latex] (b) The solid of revolution generated by revolving [latex]R[/latex] around the line [latex]x=-1.[/latex]

Note that the radius of a shell is given by [latex]x+1.[/latex] Then the volume of the solid is given by

[latex]\begin{array}{cc}\hfill V& ={\displaystyle\int }_{1}^{2}(2\pi (x+1)f(x))dx\hfill \\ & ={\displaystyle\int }_{1}^{2}(2\pi (x+1)x)dx=2\pi {\displaystyle\int }_{1}^{2}({x}^{2}+x)dx\hfill \\ & ={2\pi \left[\frac{{x}^{3}}{3}+\frac{{x}^{2}}{2}\right]|}_{1}^{2}=\frac{23\pi }{3}{\text{units}}^{3}\text{.}\hfill \end{array}[/latex]

Watch the following video to see the worked solution to the above Try It.

For our final example in this section, let’s look at the volume of a solid of revolution for which the region of revolution is bounded by the graphs of two functions.

Example: A Region of Revolution Bounded by the Graphs of Two Functions

Define [latex]R[/latex] as the region bounded above by the graph of the function [latex]f(x)=\sqrt{x}[/latex] and below by the graph of the function [latex]g(x)=\frac{1}{x}[/latex] over the interval [latex]\left[1,4\right].[/latex] Find the volume of the solid of revolution generated by revolving [latex]R[/latex] around the [latex]y\text{-axis}.[/latex]

Show Solution

First, graph the region [latex]R[/latex] and the associated solid of revolution, as shown in the following figure.

Figure 9. (a) The region [latex]R[/latex] between the graph of [latex]f(x)[/latex] and the graph of [latex]g(x)[/latex] over the interval [latex]\left[1,4\right].[/latex] (b) The solid of revolution generated by revolving [latex]R[/latex] around the [latex]y\text{-axis}.[/latex]

Note that the axis of revolution is the [latex]y\text{-axis},[/latex] so the radius of a shell is given simply by [latex]x.[/latex] We don’t need to make any adjustments to the [latex]x[/latex]-term of our integrand. The height of a shell, though, is given by [latex]f(x)-g(x),[/latex] so in this case we need to adjust the [latex]f(x)[/latex] term of the integrand. Then the volume of the solid is given by

[latex]\begin{array}{cc}\hfill V& ={\displaystyle\int }_{1}^{4}(2\pi x(f(x)-g(x)))dx\hfill \\ & ={\displaystyle\int }_{1}^{4}(2\pi x(\sqrt{x}-\frac{1}{x}))dx=2\pi {\displaystyle\int }_{1}^{4}({x}^{3\text{/}2}-1)dx\hfill \\ & ={2\pi \left[\frac{2{x}^{5\text{/}2}}{5}-x\right]|}_{1}^{4}=\frac{94\pi }{5}{\text{units}}^{3}.\hfill \end{array}[/latex]