Derivative Functions

Learning Outcomes

  • Define the derivative function of a given function

The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined. We can formally define a derivative function as follows.

Definition

Let [latex]f[/latex] be a function. The derivative function, denoted by [latex]f^{\prime}[/latex], is the function whose domain consists of those values of [latex]x[/latex] such that the following limit exists:

[latex]f^{\prime}(x)=\underset{h\to 0}{\lim}\dfrac{f(x+h)-f(x)}{h}[/latex]

 

A function [latex]f(x)[/latex] is said to be differentiable at [latex]a[/latex] if [latex]f^{\prime}(a)[/latex] exists. More generally, a function is said to be differentiable on [latex]S[/latex] if it is differentiable at every point in an open set [latex]S[/latex], and a differentiable function is one in which [latex]f^{\prime}(x)[/latex] exists on its domain.

In the next few examples we use the definition to find the derivative of a function. There are a few algebraic techniques that are commonly used when using this definition. It may be useful to recall these techniques.

Recall: Factoring out a greatest common factor

The greatest common factor (GCF) of a polynomial is the largest polynomial that divides evenly into each term of the polynomial.

When using the difference quotient, there will be many times where you will need to factor out a GCF of h. 

Recall: Rationalizing a numerator or denominator with rational and irrational terms

For a numerator or a denominator containing the sum or difference of a rational and an irrational term, multiply the numerator and denominator by the conjugate, which is found by changing the sign of the radical portion of the denominator. If the denominator is [latex]a+b\sqrt{c}[/latex], then the conjugate is [latex]a-b\sqrt{c}[/latex].

Example: Finding the Derivative of a Square-Root Function

Find the derivative of [latex]f(x)=\sqrt{x}[/latex].

Example: Finding the Derivative of a Quadratic Function

Find the derivative of the function [latex]f(x)=x^2-2x[/latex].

Try It

Find the derivative of [latex]f(x)=x^2[/latex].

Watch the following video to see the worked solution to the above Try It.

Try It

We use a variety of different notations to express the derivative of a function. In the previous example, we showed that if [latex]f(x)=x^2-2x[/latex], then [latex]f^{\prime}(x)=2x-2[/latex]. If we had expressed this function in the form [latex]y=x^2-2x[/latex], we could have expressed the derivative as [latex]y^{\prime}=2x-2[/latex] or [latex]\frac{dy}{dx}=2x-2[/latex]. We could have conveyed the same information by writing [latex]\frac{d}{dx}(x^2-2x)=2x-2[/latex]. Thus, for the function [latex]y=f(x)[/latex], each of the following notations represents the derivative of [latex]f(x)[/latex]:

[latex]f^{\prime}(x), \,\, \dfrac{dy}{dx}, \,\, y^{\prime}, \,\, \dfrac{d}{dx}(f(x))[/latex]

 

In place of [latex]f^{\prime}(a)[/latex] we may also use [latex]\frac{dy}{dx}\Big|_{x=a}[/latex] Use of the [latex]\frac{dy}{dx}[/latex] notation (called Leibniz notation) is quite common in engineering and physics. To understand this notation better, recall that the derivative of a function at a point is the limit of the slopes of secant lines as the secant lines approach the tangent line. The slopes of these secant lines are often expressed in the form [latex]\frac{\Delta y}{\Delta x}[/latex] where [latex]\Delta y[/latex] is the difference in the [latex]y[/latex] values corresponding to the difference in the [latex]x[/latex] values, which are expressed as [latex]\Delta x[/latex] (Figure 1). Thus the derivative, which can be thought of as the instantaneous rate of change of [latex]y[/latex] with respect to [latex]x[/latex], is expressed as

[latex]\dfrac{dy}{dx}=\underset{\Delta x\to 0}{\lim}\dfrac{\Delta y}{\Delta x}[/latex]

 

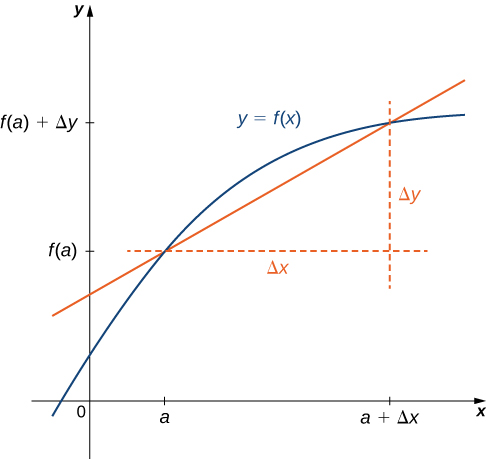
The function y = f(x) is graphed and it shows up as a curve in the first quadrant. The x-axis is marked with 0, a, and a + Δx. The y-axis is marked with 0, f(a), and f(a) + Δy. There is a straight line crossing y = f(x) at (a, f(a)) and (a + Δx, f(a) + Δy). From the point (a, f(a)), a horizontal line is drawn; from the point (a + Δx, f(a) + Δy), a vertical line is drawn. The distance from (a, f(a)) to (a + Δx, f(a)) is denoted Δx; the distance from (a + Δx, f(a) + Δy) to (a + Δx, f(a)) is denoted Δy.

Figure 1. The derivative is expressed as [latex]\frac{dy}{dx}=\underset{\Delta x\to 0}{\lim}\frac{\Delta y}{\Delta x}[/latex].