Derivatives of Various Inverse Functions

Learning Outcomes

  • Calculate the derivative of an inverse function

We begin by considering a function and its inverse. If [latex]f(x)[/latex] is both invertible and differentiable, it seems reasonable that the inverse of [latex]f(x)[/latex] is also differentiable. Figure 1 shows the relationship between a function [latex]f(x)[/latex] and its inverse [latex]f^{-1}(x)[/latex]. Look at the point [latex](a,f^{-1}(a))[/latex] on the graph of [latex]f^{-1}(x)[/latex] having a tangent line with a slope of [latex](f^{-1})^{\prime}(a)=\frac{p}{q}[/latex]. This point corresponds to a point [latex](f^{-1}(a),a)[/latex] on the graph of [latex]f(x)[/latex] having a tangent line with a slope of [latex]f^{\prime}(f^{-1}(a))=\frac{q}{p}[/latex]. Thus, if [latex]f^{-1}(x)[/latex] is differentiable at [latex]a[/latex], then it must be the case that

[latex](f^{-1})^{\prime}(a)=\dfrac{1}{f^{\prime}(f^{-1}(a))}[/latex]

 

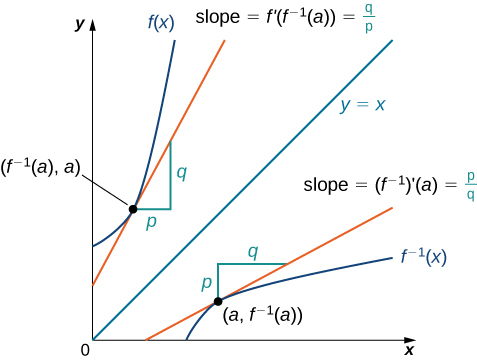
This graph shows a function f(x) and its inverse f−1(x). These functions are symmetric about the line y = x. The tangent line of the function f(x) at the point (f−1(a), a) and the tangent line of the function f−1(x) at (a, f−1(a)) are also symmetric about the line y = x. Specifically, if the slope of one were p/q, then the slope of the other would be q/p. Lastly, their derivatives are also symmetric about the line y = x.

Figure 1. The tangent lines of a function and its inverse are related; so, too, are the derivatives of these functions.

We may also derive the formula for the derivative of the inverse by first recalling that [latex]x=f(f^{-1}(x))[/latex]. Then by differentiating both sides of this equation (using the chain rule on the right), we obtain

[latex]1=f^{\prime}(f^{-1}(x))(f^{-1})^{\prime}(x))[/latex]

 

Solving for [latex](f^{-1})^{\prime}(x)[/latex], we obtain

[latex](f^{-1})^{\prime}(x)=\dfrac{1}{f^{\prime}(f^{-1}(x))}[/latex]

 

We summarize this result in the following theorem.

Inverse Function Theorem

Let [latex]f(x)[/latex] be a function that is both invertible and differentiable. Let [latex]y=f^{-1}(x)[/latex] be the inverse of [latex]f(x)[/latex]. For all [latex]x[/latex] satisfying [latex]f^{\prime}(f^{-1}(x))\ne 0[/latex],

[latex]\frac{dy}{dx}=\frac{d}{dx}(f^{-1}(x))=(f^{-1})^{\prime}(x)=\dfrac{1}{f^{\prime}(f^{-1}(x))}[/latex]

 

Alternatively, if [latex]y=g(x)[/latex] is the inverse of [latex]f(x)[/latex], then

[latex]g^{\prime}(x)=\dfrac{1}{f^{\prime}(g(x))}[/latex]

 

Example: Applying the Inverse Function Theorem, 1

Use the Inverse Function Theorem to find the derivative of [latex]g(x)=\dfrac{x+2}{x}[/latex]. Compare the resulting derivative to that obtained by differentiating the function directly.

Watch the following video to see the worked solution to Example: Applying the Inverse Function Theorem, 1.

Try It

Use the inverse function theorem to find the derivative of [latex]g(x)=\dfrac{1}{x+2}.[/latex] Compare the result obtained by differentiating [latex]g(x)[/latex] directly.

Hint

Use the preceding example as a guide.

Example: Applying the Inverse Function Theorem, 2

Use the inverse function theorem to find the derivative of [latex]g(x)=\sqrt[3]{x}[/latex].

Try It

Find the derivative of [latex]g(x)=\sqrt[5]{x}[/latex] by applying the inverse function theorem.

From the previous example, we see that we can use the inverse function theorem to extend the power rule to exponents of the form [latex]\frac{1}{n}[/latex], where [latex]n[/latex] is a positive integer. This extension will ultimately allow us to differentiate [latex]x^q[/latex], where [latex]q[/latex] is any rational number.

Extending the Power Rule to Rational Exponents

The power rule may be extended to rational exponents. That is, if [latex]n[/latex] is a positive integer, then

[latex]\frac{d}{dx}(x^{1/n})=\frac{1}{n}x^{(1/n)-1}[/latex]

 

Also, if [latex]n[/latex] is a positive integer and [latex]m[/latex] is an arbitrary integer, then

[latex]\frac{d}{dx}(x^{m/n})=\frac{m}{n}x^{(m/n)-1}[/latex]

 

Proof

The function [latex]g(x)=x^{1/n}[/latex] is the inverse of the function [latex]f(x)=x^n[/latex]. Since [latex]g^{\prime}(x)=\dfrac{1}{f^{\prime}(g(x))}[/latex], begin by finding [latex]f^{\prime}(x)[/latex]. Thus,

[latex]f^{\prime}(x)=nx^{n-1}[/latex] and [latex]f^{\prime}(g(x))=n(x^{1/n})^{n-1}=nx^{(n-1)/n}[/latex].

 

Finally,

[latex]g^{\prime}(x)=\dfrac{1}{nx^{(n-1)/n}}=\frac{1}{n}x^{(1-n)/n}=\frac{1}{n}x^{(1/n)-1}[/latex].

 

To differentiate [latex]x^{m/n}[/latex] we must rewrite it as [latex](x^{1/n})^m[/latex] and apply the chain rule. Thus,

[latex]\frac{d}{dx}(x^{m/n})=\frac{d}{dx}((x^{1/n})^m)=m(x^{1/n})^{m-1} \cdot \frac{1}{n}x^{(1/n)-1}=\frac{m}{n}x^{(m/n)-1}[/latex].
[latex]_\blacksquare[/latex]

Example: Applying the Power Rule to a Rational Power

Find the equation of the line tangent to the graph of [latex]y=x^{\frac{2}{3}}[/latex] at [latex]x=8[/latex].

Watch the following video to see the worked solution to Example: Applying the Power Rule to a Rational Power.

Try It

Find the derivative of [latex]s(t)=\sqrt{2t+1}[/latex].

Try It