Finding the Derivative Using Implicit Differentiation

Learning Outcomes

  • Recognize the difference between an implicit function and an explicit function
  • Find the derivative of a complicated function by using implicit differentiation
  • Use implicit differentiation to determine the equation of a tangent line

What is Implicit Differentiation?

In most discussions of math, if the dependent variable [latex]y[/latex] is a function of the independent variable [latex]x[/latex], we express [latex]y[/latex] in terms of [latex]x[/latex]. If this is the case, we say that [latex]y[/latex] is an explicit function of [latex]x[/latex]. For example, when we write the equation [latex]y=x^2+1[/latex], we are defining [latex]y[/latex] explicitly in terms of [latex]x[/latex]. On the other hand, if the relationship between the function [latex]y[/latex] and the variable [latex]x[/latex] is expressed by an equation where [latex]y[/latex] is not expressed entirely in terms of [latex]x[/latex], we say that the equation defines [latex]y[/latex] implicitly in terms of [latex]x[/latex]. For example, the equation [latex]y-x^2=1[/latex] defines the function [latex]y=x^2+1[/latex] implicitly.

Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). We are using the idea that portions of [latex]y[/latex] are functions that satisfy the given equation, but that [latex]y[/latex] is not actually a function of [latex]x[/latex].

In general, an equation defines a function implicitly if the function satisfies that equation. An equation may define many different functions implicitly. For example, the functions

[latex]y=\sqrt{25-x^2}[/latex],  [latex]y = -\sqrt{25-x^2}[/latex], and [latex]y=\begin{cases} \sqrt{25-x^2} & \text{ if } \, -5 \le x < 0 \\ -\sqrt{25-x^2} & \text{ if } \, 0 \le x \le 5 \end{cases}[/latex],

which are illustrated in Figure 1, are just three of the many functions defined implicitly by the equation [latex]x^2+y^2=25[/latex].

 

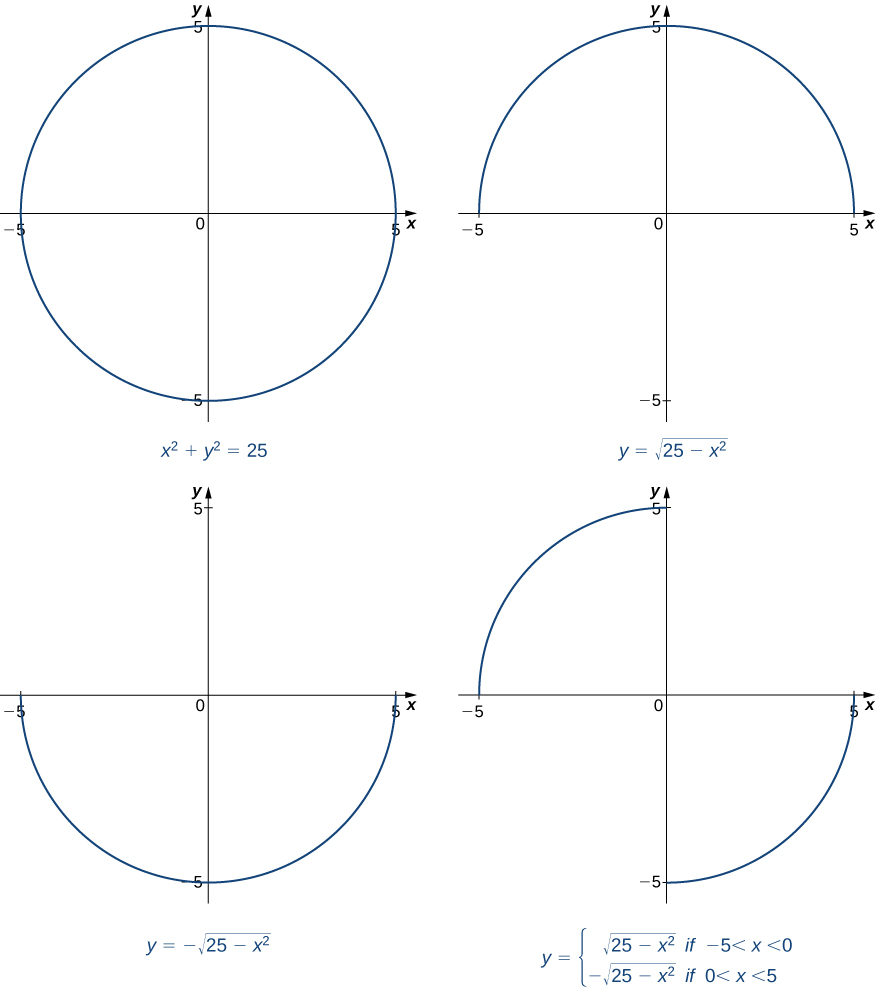
The circle with radius 5 and center at the origin is graphed fully in one picture. Then, only its segments in quadrants I and II are graphed. Then, only its segments in quadrants III and IV are graphed. Lastly, only its segments in quadrants II and IV are graphed.

Figure 1. The equation [latex]{x}^{2}+{y}^{2}=25[/latex] defines many functions implicitly.

If we want to find the slope of the line tangent to the graph of [latex]x^2+y^2=25[/latex] at the point [latex](3,4)[/latex], we could evaluate the derivative of the function [latex]y=\sqrt{25-x^2}[/latex] at [latex]x=3[/latex]. On the other hand, if we want the slope of the tangent line at the point [latex](3,-4)[/latex], we could use the derivative of [latex]y=−\sqrt{25-x^2}[/latex]. However, it is not always easy to solve for a function defined implicitly by an equation. Fortunately, the technique of implicit differentiation allows us to find the derivative of an implicitly defined function without ever solving for the function explicitly. The process of finding [latex]\frac{dy}{dx}[/latex] using implicit differentiation is described in the following problem-solving strategy.

Problem-Solving Strategy: Implicit Differentiation

To perform implicit differentiation on an equation that defines a function [latex]y[/latex] implicitly in terms of a variable [latex]x[/latex], use the following steps:

  1. Take the derivative of both sides of the equation. Keep in mind that [latex]y[/latex] is a function of [latex]x[/latex]. Consequently, whereas [latex]\frac{d}{dx}(\sin x)= \cos x, \, \frac{d}{dx}(\sin y)= \cos y\frac{dy}{dx}[/latex] because we must use the Chain Rule to differentiate [latex]\sin y[/latex] with respect to [latex]x[/latex].
  2. Rewrite the equation so that all terms containing [latex]\frac{dy}{dx}[/latex] are on the left and all terms that do not contain [latex]\frac{dy}{dx}[/latex] are on the right.
  3. Factor out [latex]\frac{dy}{dx}[/latex] on the left.
  4. Solve for [latex]\frac{dy}{dx}[/latex] by dividing both sides of the equation by an appropriate algebraic expression.

Example: Using Implicit Differentiation

Assuming that [latex]y[/latex] is defined implicitly by the equation [latex]x^2+y^2=25[/latex], find [latex]\frac{dy}{dx}[/latex].

Example: Using Implicit Differentiation and the Product Rule

Assuming that [latex]y[/latex] is defined implicitly by the equation [latex]x^3 \sin y+y=4x+3[/latex], find [latex]\frac{dy}{dx}[/latex].

Example: Using Implicit Differentiation to Find a Second Derivative

Find [latex]\frac{d^2 y}{dx^2}[/latex] if [latex]x^2+y^2=25[/latex].

Watch the following video to see the worked solution to Example: Using Implicit Differentiation to Find a Second Derivative.

Try It

Find [latex]\frac{dy}{dx}[/latex] for [latex]y[/latex] defined implicitly by the equation [latex]4x^5+ \tan y=y^2+5x[/latex].

Try It

Finding Tangent Lines Implicitly

Now that we have seen the technique of implicit differentiation, we can apply it to the problem of finding equations of tangent lines to curves described by equations.

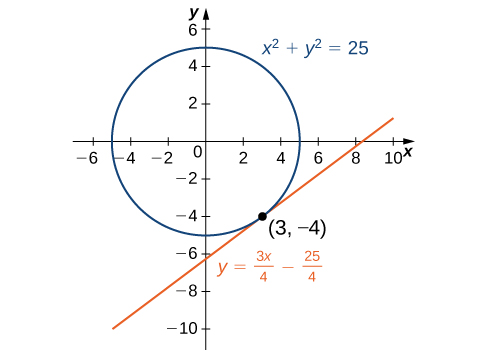
Example: Finding a Tangent Line to a Circle

Find the equation of the line tangent to the curve [latex]x^2+y^2=25[/latex] at the point [latex](3,-4)[/latex].

Example: Finding the Equation of the Tangent Line to a Curve

Find the equation of the line tangent to the graph of [latex]y^3+x^3-3xy=0[/latex] at the point [latex]\left(\frac{3}{2},\frac{3}{2}\right)[/latex] (Figure 3). This curve is known as the folium (or leaf) of Descartes.

A folium is shown, which is a line that creates a loop that crosses over itself. In this graph, it crosses over itself at (0, 0). Its tangent line from (3/2, 3/2) is shown.

Figure 3. Finding the tangent line to the folium of Descartes at [latex](\frac{3}{2},\frac{3}{2})[/latex].

Example: Applying Implicit Differentiation

In a simple video game, a rocket travels in an elliptical orbit whose path is described by the equation [latex]4x^2+25y^2=100[/latex]. The rocket can fire missiles along lines tangent to its path. The object of the game is to destroy an incoming asteroid traveling along the positive [latex]x[/latex]-axis toward [latex](0,0)[/latex]. If the rocket fires a missile when it is located at [latex]\left(3,\frac{8}{5}\right)[/latex], where will it intersect the [latex]x[/latex]-axis?

Watch the following video to see the worked solution to Example: Finding the Equation of the Tangent Line to a Curve.

Try It

Find the equation of the line tangent to the hyperbola [latex]x^2-y^2=16[/latex] at the point [latex](5,3)[/latex].