Graphs and Periods of the Trigonometric Functions

Learning Outcomes

  • Identify the graphs and periods of the trigonometric functions
  • Describe the shift of a sine or cosine graph from the equation of the function

We have seen that as we travel around the unit circle, the values of the trigonometric functions repeat. We can see this pattern in the graphs of the functions. Let [latex]P=(x,y)[/latex] be a point on the unit circle and let [latex]\theta[/latex] be the corresponding angle.  Since the angle [latex]\theta[/latex] and [latex]\theta +2\pi[/latex] correspond to the same point [latex]P[/latex], the values of the trigonometric functions at [latex]\theta[/latex] and at [latex]\theta +2\pi[/latex] are the same. Consequently, the trigonometric functions are periodic functions. The period of a function [latex]f[/latex] is defined to be the smallest positive value [latex]p[/latex] such that [latex]f(x+p)=f(x)[/latex] for all values [latex]x[/latex] in the domain of [latex]f[/latex]. The sine, cosine, secant, and cosecant functions have a period of [latex]2\pi[/latex]. Since the tangent and cotangent functions repeat on an interval of length [latex]\pi[/latex], their period is [latex]\pi[/latex] (Figure 9).

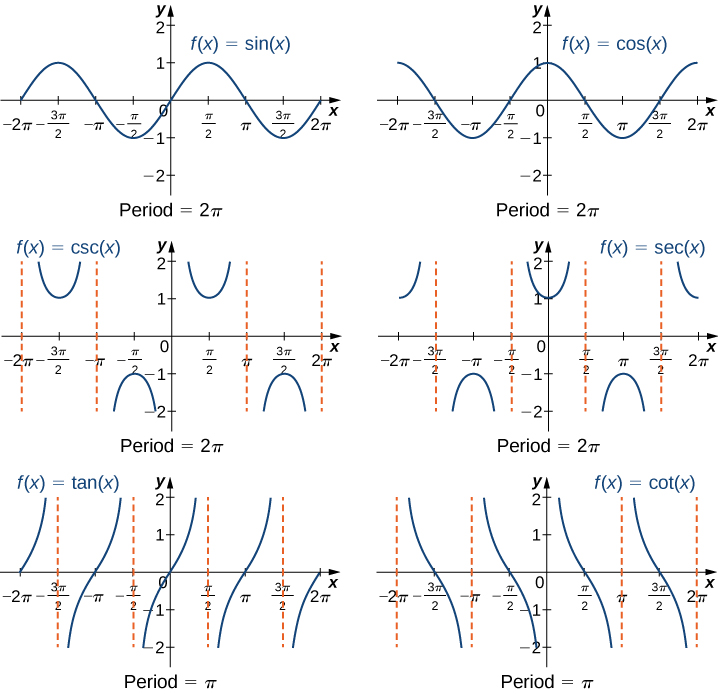
An image of six graphs. Each graph has an x axis that runs from -2 pi to 2 pi and a y axis that runs from -2 to 2. The first graph is of the function “f(x) = sin(x)”, which is a curved wave function. The graph of the function starts at the point (-2 pi, 0) and increases until the point (-((3 pi)/2), 1). After this point, the function decreases until the point (-(pi/2), -1). After this point, the function increases until the point ((pi/2), 1). After this point, the function decreases until the point (((3 pi)/2), -1). After this point, the function begins to increase again. The x intercepts shown on the graph are at the points (-2 pi, 0), (-pi, 0), (0, 0), (pi, 0), and (2 pi, 0). The y intercept is at the origin. The second graph is of the function “f(x) = cos(x)”, which is a curved wave function. The graph of the function starts at the point (-2 pi, 1) and decreases until the point (-pi, -1). After this point, the function increases until the point (0, 1). After this point, the function decreases until the point (pi, -1). After this point, the function increases again. The x intercepts shown on the graph are at the points (-((3 pi)/2), 0), (-(pi/2), 0), ((pi/2), 0), and (((3 pi)/2), 0). The y intercept is at the point (0, 1). The graph of cos(x) is the same as the graph of sin(x), except it is shifted to the left by a distance of (pi/2). On the next four graphs there are dotted vertical lines which are not a part of the function, but act as boundaries for the function, boundaries the function will never touch. They are known as vertical asymptotes. There are infinite vertical asymptotes for all of these functions, but these graphs only show a few. The third graph is of the function “f(x) = csc(x)”. The vertical asymptotes for “f(x) = csc(x)” on this graph occur at “x = -2 pi”, “x = -pi”, “x = 0”, “x = pi”, and “x = 2 pi”. Between the “x = -2 pi” and “x = -pi” asymptotes, the function looks like an upward facing “U”, with a minimum at the point (-((3 pi)/2), 1). Between the “x = -pi” and “x = 0” asymptotes, the function looks like an downward facing “U”, with a maximum at the point (-(pi/2), -1). Between the “x = 0” and “x = pi” asymptotes, the function looks like an upward facing “U”, with a minimum at the point ((pi/2), 1). Between the “x = pi” and “x = 2 pi” asymptotes, the function looks like an downward facing “U”, with a maximum at the point (((3 pi)/2), -1). The fourth graph is of the function “f(x) = sec(x)”. The vertical asymptotes for this function on this graph are at “x = -((3 pi)/2)”, “x = -(pi/2)”, “x = (pi/2)”, and “x = ((3 pi)/2)”. Between the “x = -((3 pi)/2)” and “x = -(pi/2)” asymptotes, the function looks like an downward facing “U”, with a maximum at the point (-pi, -1). Between the “x = -(pi/2)” and “x = (pi/2)” asymptotes, the function looks like an upward facing “U”, with a minimum at the point (0, 1). Between the “x = (pi/2)” and “x = (3pi/2)” asymptotes, the function looks like an downward facing “U”, with a maximum at the point (pi, -1). The graph of sec(x) is the same as the graph of csc(x), except it is shifted to the left by a distance of (pi/2). The fifth graph is of the function “f(x) = tan(x)”. The vertical asymptotes of this function on this graph occur at “x = -((3 pi)/2)”, “x = -(pi/2)”, “x = (pi/2)”, and “x = ((3 pi)/2)”. In between all of the vertical asymptotes, the function is always increasing but it never touches the asymptotes. The x intercepts on this graph occur at the points (-2 pi, 0), (-pi, 0), (0, 0), (pi, 0), and (2 pi, 0). The y intercept is at the origin. The sixth graph is of the function “f(x) = cot(x)”. The vertical asymptotes of this function on this graph occur at “x = -2 pi”, “x = -pi”, “x = 0”, “x = pi”, and “x = 2 pi”. In between all of the vertical asymptotes, the function is always decreasing but it never touches the asymptotes. The x intercepts on this graph occur at the points (-((3 pi)/2), 0), (-(pi/2), 0), ((pi/2), 0), and (((3 pi)/2), 0) and there is no y intercept.

Figure 9. The six trigonometric functions are periodic.

Try It

Transformations to Trigonometric Graphs

Just as with algebraic functions, we can apply transformations to trigonometric functions. In particular, consider the following function:

[latex]f(x)=A \sin(B(x-\alpha))+C[/latex]

 

In Figure 10, the constant [latex]\alpha[/latex] causes a horizontal or phase shift. The factor [latex]B[/latex] changes the period. This transformed sine function will have a period [latex]2\pi / |B|[/latex]. The factor [latex]A[/latex] results in a vertical stretch by a factor of [latex]|A|[/latex]. We say [latex]|A|[/latex] is the “amplitude of [latex]f[/latex].” The constant [latex]C[/latex] causes a vertical shift.

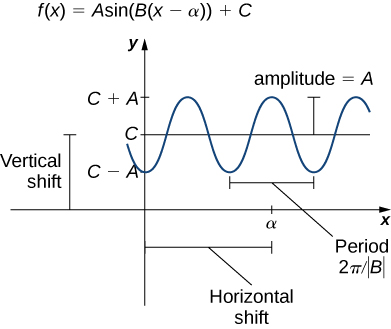
An image of a graph. The graph is of the function “f(x) = Asin(B(x - alpha)) + C”. Along the y axis, there are 3 hash marks: starting from the bottom and moving up, the hash marks are at the values “C - A”, “C”, and “C + A”. The distance from the origin to “C” is labeled “vertical shift”. The distance from “C - A” to “A” and the distance from “A” to “C + A” is “A”, which is labeled “amplitude”. On the x axis is a hash mark at the value “alpha” and the distance between the origin and “alpha” is labeled “horizontal shift”. The distance between two successive minimum values of the function (in other words, the distance between two bottom parts of the wave that are next to each other) is “(2 pi)/(absolute value of B)” is labeled the period. The period is also the distance between two successive maximum values of the function.

Figure 10. A graph of a general sine function.

Notice in Figure 9 that the graph of [latex]y=\cos x[/latex] is the graph of [latex]y=\sin x[/latex] shifted to the left [latex]\pi /2[/latex] units. Therefore, we can write [latex]\cos x=\sin(x+\pi /2)[/latex]. Similarly, we can view the graph of [latex]y=\sin x[/latex] as the graph of [latex]y=\cos x[/latex] shifted right [latex]\pi /2[/latex] units, and state that [latex]\sin x=\cos(x-\pi /2)[/latex].

A shifted sine curve arises naturally when graphing the number of hours of daylight in a given location as a function of the day of the year. For example, suppose a city reports that June 21 is the longest day of the year with 15.7 hours and December 21 is the shortest day of the year with 8.3 hours. It can be shown that the function

[latex]h(t)=3.7\sin(\frac{2\pi}{365}(t-80.5))+12[/latex]

 

is a model for the number of hours of daylight [latex]h[/latex] as a function of day of the year [latex]t[/latex] (Figure 11).

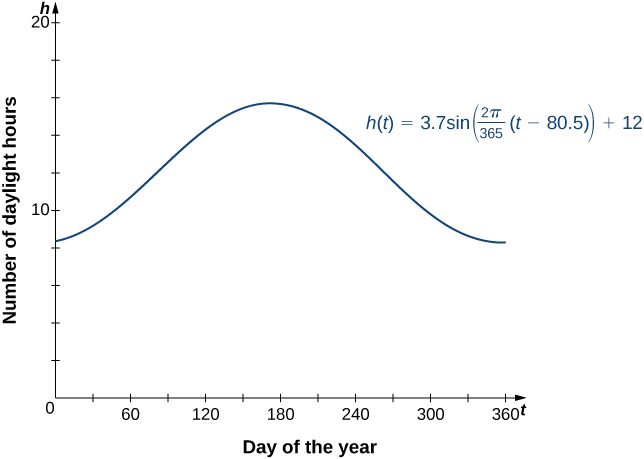
An image of a graph. The x axis runs from 0 to 365 and is labeled “t, day of the year”. The y axis runs from 0 to 20 and is labeled “h, number of daylight hours”. The graph is of the function “h(t) = 3.7sin(((2 pi)/365)(t - 80.5)) + 12”, which is a curved wave function. The function starts at the approximate point (0, 8.4) and begins increasing until the approximate point (171.8, 15.7). After this point, the function decreases until the approximate point (354.3, 8.3). After this point, the function begins increasing again.

Figure 11. The hours of daylight as a function of day of the year can be modeled by a shifted sine curve.

Example: Sketching the Graph of a Transformed Sine Curve

Sketch a graph of [latex]f(x)=3\sin(2(x-\frac{\pi}{4}))+1[/latex].

Watch the following video to see the worked solution to Example: Sketching the Graph of a Transformed Sine Curve

Try It

Describe the relationship between the graph of [latex]f(x)=3\sin(4x)-5[/latex] and the graph of [latex]y=\sin x[/latex].

Try It