Inverse Functions

Learning Outcomes

  • Determine the conditions for when a function has an inverse
  • Use the horizontal line test to recognize when a function is one-to-one
  • Find the inverse of a given function
  • Draw the graph of an inverse function

Existence of an Inverse Function

We begin with an example. Given a function [latex]f[/latex] and an output [latex]y=f(x)[/latex], we are often interested in finding what value or values [latex]x[/latex] were mapped to [latex]y[/latex] by [latex]f[/latex]. For example, consider the function [latex]f(x)=x^3+4[/latex]. Since any output [latex]y=x^3+4[/latex], we can solve this equation for [latex]x[/latex] to find that the input is [latex]x=\sqrt[3]{y-4}[/latex]. This equation defines [latex]x[/latex] as a function of [latex]y[/latex]. Denoting this function as [latex]f^{-1}[/latex], and writing [latex]x=f^{-1}(y)=\sqrt[3]{y-4}[/latex], we see that for any [latex]x[/latex] in the domain of [latex]f, \, f^{-1}(f(x))=f^{-1}(x^3+4)=x[/latex]. Thus, this new function, [latex]f^{-1}[/latex], “undid” what the original function [latex]f[/latex] did. A function with this property is called the inverse function of the original function.

Definition

Given a function [latex]f[/latex] with domain [latex]D[/latex] and range [latex]R[/latex], its inverse function (if it exists) is the function [latex]f^{-1}[/latex] with domain [latex]R[/latex] and range [latex]D[/latex] such that [latex]f^{-1}(y)=x[/latex] if [latex]f(x)=y[/latex]. In other words, for a function [latex]f[/latex] and its inverse [latex]f^{-1}[/latex],

[latex]f^{-1}(f(x))=x[/latex] for all [latex]x[/latex] in [latex]D[/latex], and [latex]f(f^{-1}(y))=y[/latex] for all [latex]y[/latex] in [latex]R[/latex]

Note that [latex]f^{-1}[/latex] is read as “f inverse.” Here, the -1 is not used as an exponent and [latex]f^{-1}(x) \ne 1/f(x)[/latex]. Figure 1 shows the relationship between the domain and range of [latex]f[/latex] and the domain and range of [latex]f^{-1}[/latex].

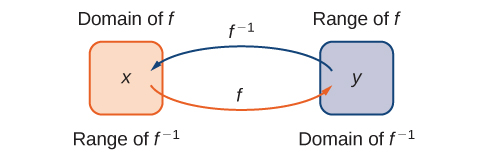
An image of two bubbles. The first bubble is orange and has two labels: the top label is “Domain of f” and the bottom label is “Range of f inverse”. Within this bubble is the variable “x”. An orange arrow with the label “f” points from this bubble to the second bubble. The second bubble is blue and has two labels: the top label is “range of f” and the bottom label is “domain of f inverse”. Within this bubble is the variable “y”. A blue arrow with the label “f inverse” points from this bubble to the first bubble.

Figure 1. Given a function [latex]f[/latex] and its inverse [latex]f^{-1}, \, f^{-1}(y)=x[/latex] if and only if [latex]f(x)=y[/latex]. The range of [latex]f[/latex] becomes the domain of [latex]f^{-1}[/latex] and the domain of [latex]f[/latex] becomes the range of [latex]f^{-1}[/latex].

Recall that a function has exactly one output for each input. Remember the vertical line test?

Recall: THe vertical line test

We can identify whether the graph of a relation represents a function because for each [latex]x[/latex]-coordinate there will be exactly one [latex]y[/latex]-coordinate.

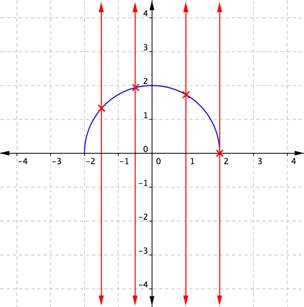
A graph of a semicircle. Four vertical lines cross the semicircle at one point each.

Figure 2. Semicircle graph undergoing the vertical line test.

When a vertical line is placed across the plot of this relation, it does not intersect the graph more than once for any values of [latex]x[/latex]. This is a graph of a function.

If, on the other hand, a graph shows two or more intersections with a vertical line, then an input ([latex]x[/latex]-coordinate) can have more than one output ([latex]y[/latex]-coordinate), and [latex]y[/latex] is not a function of [latex]x[/latex]. Examining the graph of a relation to determine if a vertical line would intersect with more than one point is a quick way to determine if the relation shown by the graph is a function.

Therefore, to define an inverse function, we need to map each input to exactly one output. For example, let’s try to find the inverse function for [latex]f(x)=x^2[/latex]. Solving the equation [latex]y=x^2[/latex] for [latex]x[/latex], we arrive at the equation [latex]x= \pm \sqrt{y}[/latex]. This equation does not describe [latex]x[/latex] as a function of [latex]y[/latex] because there are two solutions to this equation for every [latex]y>0[/latex]. The problem with trying to find an inverse function for [latex]f(x)=x^2[/latex] is that two inputs are sent to the same output for each output [latex]y>0[/latex]. The function [latex]f(x)=x^3+4[/latex] discussed earlier did not have this problem. For that function, each input was sent to a different output. A function that sends each input to a different output is called a one-to-one function.

Try It

Definition

We say a [latex]f[/latex] is a one-to-one function if [latex]f(x_1) \ne f(x_2)[/latex] when [latex]x_1 \ne x_2[/latex].

One way to determine whether a function is one-to-one is by looking at its graph. If a function is one-to-one, then no two inputs can be sent to the same output. Therefore, if we draw a horizontal line anywhere in the [latex]xy[/latex]-plane, according to the horizontal line test, it cannot intersect the graph more than once. We note that the horizontal line test is different from the vertical line test. The vertical line test determines whether a graph is the graph of a function. The horizontal line test determines whether a function is one-to-one (Figure 3).

Horizontal Line Test

A function [latex]f[/latex] is one-to-one if and only if every horizontal line intersects the graph of [latex]f[/latex] no more than once.

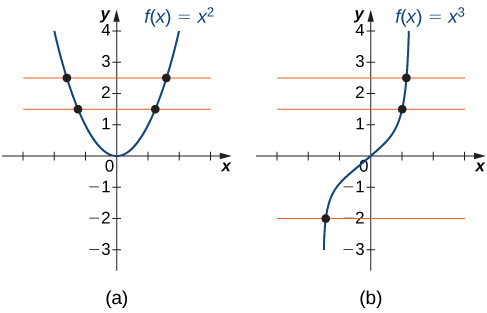
An image of two graphs. Both graphs have an x axis that runs from -3 to 3 and a y axis that runs from -3 to 4. The first graph is of the function “f(x) = x squared”, which is a parabola. The function decreases until it hits the origin, where it begins to increase. The x intercept and y intercept are both at the origin. There are two orange horizontal lines also plotted on the graph, both of which run through the function at two points each. The second graph is of the function “f(x) = x cubed”, which is an increasing curved function. The x intercept and y intercept are both at the origin. There are three orange lines also plotted on the graph, each of which only intersects the function at one point.

Figure 3. (a) The function [latex]f(x)=x^2[/latex] is not one-to-one because it fails the horizontal line test. (b) The function [latex]f(x)=x^3[/latex] is one-to-one because it passes the horizontal line test.

Example: Determining Whether a Function Is One-to-One

For each of the following functions, use the horizontal line test to determine whether it is one-to-one.

a.

An image of a graph. The x axis runs from -3 to 11 and the y axis runs from -3 to 11. The graph is of a step function which contains 10 horizontal steps. Each steps starts with a closed circle and ends with an open circle. The first step starts at the origin and ends at the point (1, 0). The second step starts at the point (1, 1) and ends at the point (1, 2). Each of the following 8 steps starts 1 unit higher in the y direction than where the previous step ended. The tenth and final step starts at the point (9, 9) and ends at the point (10, 9)

Figure 4. Is this function one-to-one?

b.

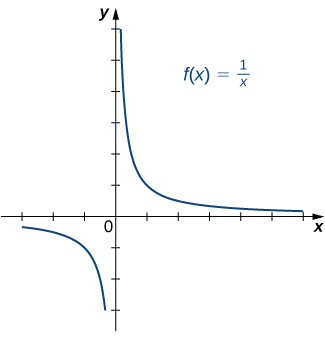
An image of a graph. The x axis runs from -3 to 6 and the y axis runs from -3 to 6. The graph is of the function “f(x) = (1/x)”, a curved decreasing function. The graph of the function starts right below the x axis in the 4th quadrant and begins to decreases until it comes close to the y axis. The graph keeps decreasing as it gets closer and closer to the y axis, but never touches it due to the vertical asymptote. In the first quadrant, the graph of the function starts close to the y axis and keeps decreasing until it gets close to the x axis. As the function continues to decreases it gets closer and closer to the x axis without touching it, where there is a horizontal asymptote.

Figure 5. Is this function one-to-one?

Try It

Is the function [latex]f[/latex] graphed in the following image one-to-one?

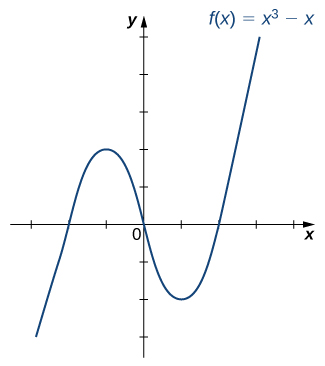
An image of a graph. The x axis runs from -3 to 4 and the y axis runs from -3 to 5. The graph is of the function “f(x) = (x cubed) - x” which is a curved function. The function increases, decreases, then increases again. The x intercepts are at the points (-1, 0), (0,0), and (1, 0). The y intercept is at the origin.

Figure 8. Is this function one-to-one?

Try It

Finding a Function’s Inverse

We can now consider one-to-one functions and show how to find their inverses. Recall that a function maps elements in the domain of [latex]f[/latex] to elements in the range of [latex]f[/latex]. The inverse function maps each element from the range of [latex]f[/latex] back to its corresponding element from the domain of [latex]f[/latex]. Therefore, to find the inverse function of a one-to-one function [latex]f[/latex], given any [latex]y[/latex] in the range of [latex]f[/latex], we need to determine which [latex]x[/latex] in the domain of [latex]f[/latex] satisfies [latex]f(x)=y[/latex]. Since [latex]f[/latex] is one-to-one, there is exactly one such value [latex]x[/latex]. We can find that value [latex]x[/latex] by solving the equation [latex]f(x)=y[/latex] for [latex]x[/latex]. Doing so, we are able to write [latex]x[/latex] as a function of [latex]y[/latex] where the domain of this function is the range of [latex]f[/latex] and the range of this new function is the domain of [latex]f[/latex]. Consequently, this function is the inverse of [latex]f[/latex], and we write [latex]x=f^{-1}(y)[/latex]. Since we typically use the variable [latex]x[/latex] to denote the independent variable and [latex]y[/latex] to denote the dependent variable, we often interchange the roles of [latex]x[/latex] and [latex]y[/latex], and write [latex]y=f^{-1}(x)[/latex]. Representing the inverse function in this way is also helpful later when we graph a function [latex]f[/latex] and its inverse [latex]f^{-1}[/latex] on the same axes.

Problem-Solving Strategy, Finding an Inverse Function

  1. Solve the equation [latex]y=f(x)[/latex] for [latex]x[/latex].
  2. Interchange the variables [latex]x[/latex] and [latex]y[/latex] and write [latex]y=f^{-1}(x)[/latex].

To complete the first step to finding an inverse function, we recall isolating a variable in a given equation.

Recall: isolate a variable in a formula

Isolate the variable for width [latex]w[/latex] from the formula for the perimeter of a rectangle:  

[latex]{P}=2\left({l}\right)+2\left({w}\right)[/latex].

First, isolate the term with [latex]w[/latex] by subtracting [latex]2l[/latex] from both sides of the equation.

[latex] \displaystyle \begin{array}{l}\,\,\,\,\,\,\,\,\,\,P\,=\,\,\,\,2l+2w\\\underline{\,\,\,\,\,-2l\,\,\,\,\,-2l\,\,\,\,\,\,\,\,\,\,\,}\\P-2l=\,\,\,\,\,\,\,\,\,\,\,\,\,2w\end{array}[/latex]

Next, clear the coefficient of [latex]w[/latex] by dividing both sides of the equation by [latex]2[/latex].

[latex]\displaystyle \begin{array}{l}\underline{P-2l}=\underline{2w}\\\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\\ \,\,\,\dfrac{P-2l}{2}\,\,=\,\,w\\\,\,\,\,\,\,\,\,\,\,\,w=\dfrac{P-2l}{2}\end{array}[/latex]

You can rewrite the equation so the isolated variable is on the left side.

[latex]w=\Large\frac{P-2l}{2}[/latex]

Example: Finding an Inverse Function

Find the inverse for the function [latex]f(x)=3x-4[/latex]. State the domain and range of the inverse function. Verify that [latex]f^{-1}(f(x))=x[/latex].

Watch the following video to see the worked solution to Example: Finding an Inverse Function

Try It

Find the inverse of the function [latex]f(x)=\dfrac{3x}{(x-2)}[/latex]. State the domain and range of the inverse function.

Try It

Graphing Inverse Functions

Let’s consider the relationship between the graph of a function [latex]f[/latex] and the graph of its inverse. Consider the graph of [latex]f[/latex] shown in Figure 9(a) and a point [latex](a,b)[/latex] on the graph. Since [latex]b=f(a)[/latex], then [latex]f^{-1}(b)=a[/latex]. Therefore, when we graph [latex]f^{-1}[/latex], the point [latex](b,a)[/latex] is on the graph. As a result, the graph of [latex]f^{-1}[/latex] is a reflection of the graph of [latex]f[/latex] about the line [latex]y=x[/latex].

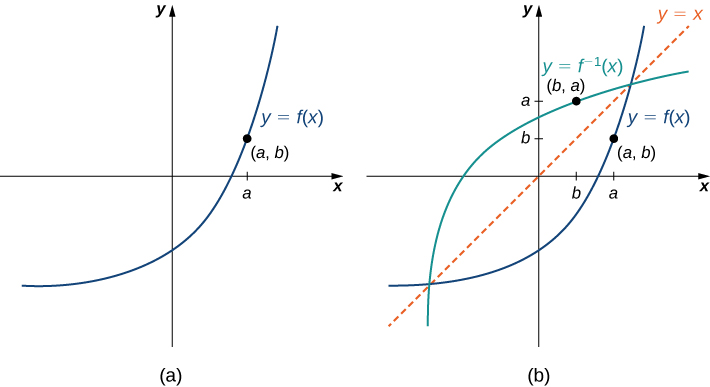
An image of two graphs. The first graph is of “y = f(x)”, which is a curved increasing function, that increases at a faster rate as x increases. The point (a, b) is on the graph of the function in the first quadrant. The second graph also graphs “y = f(x)” with the point (a, b), but also graphs the function “y = f inverse (x)”, an increasing curved function, that increases at a slower rate as x increases. This function includes the point (b, a). In addition to the two functions, there is a diagonal dotted line potted with the equation “y =x”, which shows that “f(x)” and “f inverse (x)” are mirror images about the line “y =x”.

Figure 9. (a) The graph of this function [latex]f[/latex] shows point [latex](a,b)[/latex] on the graph of [latex]f[/latex]. (b) Since [latex](a,b)[/latex] is on the graph of [latex]f[/latex], the point [latex](b,a)[/latex] is on the graph of [latex]f^{-1}[/latex]. The graph of [latex]f^{-1}[/latex] is a reflection of the graph of [latex]f[/latex] about the line [latex]y=x[/latex].

Example: Sketching Graphs of Inverse Functions

For the graph of [latex]f[/latex] in the following image, sketch a graph of [latex]f^{-1}[/latex] by sketching the line [latex]y=x[/latex] and using symmetry. Identify the domain and range of [latex]f^{-1}[/latex].

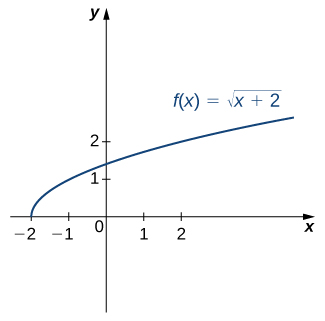
An image of a graph. The x axis runs from -2 to 2 and the y axis runs from 0 to 2. The graph is of the function “f(x) = square root of (x +2)”, an increasing curved function. The function starts at the point (-2, 0). The x intercept is at (-2, 0) and the y intercept is at the approximate point (0, 1.4).

Figure 10. Graph of [latex]f(x)[/latex].

Try It

Sketch the graph of [latex]f(x)=2x+3[/latex] and the graph of its inverse using the symmetry property of inverse functions.

Try It

Restricting Domains

As we have seen, [latex]f(x)=x^2[/latex] does not have an inverse function because it is not one-to-one. However, we can choose a subset of the domain of [latex]f[/latex] such that the function is one-to-one. This subset is called a restricted domain. By restricting the domain of [latex]f[/latex], we can define a new function [latex]g[/latex] such that the domain of [latex]g[/latex] is the restricted domain of [latex]f[/latex] and [latex]g(x)=f(x)[/latex] for all [latex]x[/latex] in the domain of [latex]g[/latex]. Then we can define an inverse function for [latex]g[/latex] on that domain. For example, since [latex]f(x)=x^2[/latex] is one-to-one on the interval [latex][0,\infty)[/latex], we can define a new function [latex]g[/latex] such that the domain of [latex]g[/latex] is [latex][0,\infty)[/latex] and [latex]g(x)=x^2[/latex] for all [latex]x[/latex] in its domain. Since [latex]g[/latex] is a one-to-one function, it has an inverse function, given by the formula [latex]g^{-1}(x)=\sqrt{x}[/latex]. On the other hand, the function [latex]f(x)=x^2[/latex] is also one-to-one on the domain [latex](−\infty,0][/latex]. Therefore, we could also define a new function [latex]h[/latex] such that the domain of [latex]h[/latex] is [latex](−\infty,0][/latex] and [latex]h(x)=x^2[/latex] for all [latex]x[/latex] in the domain of [latex]h[/latex]. Then [latex]h[/latex] is a one-to-one function and must also have an inverse. Its inverse is given by the formula [latex]h^{-1}(x)=−\sqrt{x}[/latex] (Figure 13).

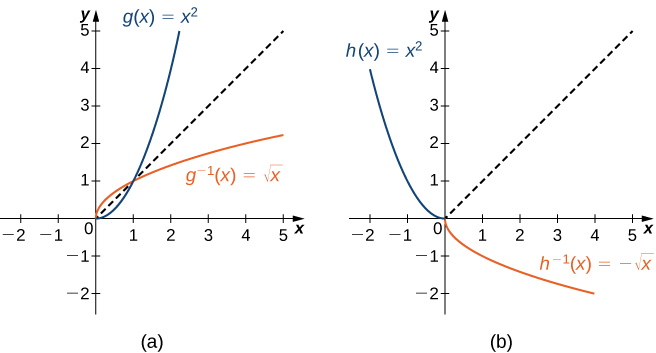
An image of two graphs. Both graphs have an x axis that runs from -2 to 5 and a y axis that runs from -2 to 5. The first graph is of two functions. The first function is “g(x) = x squared”, an increasing curved function that starts at the point (0, 0). This function increases at a faster rate for larger values of x. The second function is “g inverse (x) = square root of x”, an increasing curved function that starts at the point (0, 0). This function increases at a slower rate for larger values of x. The first function is “h(x) = x squared”, a decreasing curved function that ends at the point (0, 0). This function decreases at a slower rate for larger values of x. The second function is “h inverse (x) = -(square root of x)”, an increasing curved function that starts at the point (0, 0). This function decreases at a slower rate for larger values of x. In addition to the two functions, there is a diagonal dotted line potted with the equation “y =x”, which shows that “f(x)” and “f inverse (x)” are mirror images about the line “y =x”.

Figure 13. (a) For [latex]g(x)=x^2[/latex] restricted to [latex][0,\infty), \, g^{-1}(x)=\sqrt{x}[/latex]. (b) For [latex]h(x)=x^2[/latex] restricted to [latex](−\infty,0], \, h^{-1}(x)=−\sqrt{x}[/latex].

Example: Restricting the Domain

Consider the function [latex]f(x)=(x+1)^2[/latex].

  1. Sketch the graph of [latex]f[/latex] and use the horizontal line test to show that [latex]f[/latex] is not one-to-one.
  2. Show that [latex]f[/latex] is one-to-one on the restricted domain [latex][-1,\infty)[/latex]. Determine the domain and range for the inverse of [latex]f[/latex] on this restricted domain and find a formula for [latex]f^{-1}[/latex].

Watch the following video to see the worked solution to Example: Restricting the Domain

Try It

Consider [latex]f(x)=\dfrac{1}{x^2}[/latex] restricted to the domain [latex](−\infty ,0)[/latex]. Verify that [latex]f[/latex] is one-to-one on this domain. Determine the domain and range of the inverse of [latex]f[/latex] and find a formula for [latex]f^{-1}[/latex].