Learning Outcomes
- Convert from logarithmic form to exponential form
- Define and use the power rule for logarithms to rewrite expressions
In the L’Hopital’s Rule section, some of the concepts require working with natural logarithms. Here we will review how to convert from logarithmic to exponential form in addition to the power property for logarithms.
Convert from Logarithmic to Exponential Form
We can express the relationship between logarithmic form and its corresponding exponential form as follows:
[latex]{\mathrm{log}}_{b}\left(x\right)=y\Leftrightarrow {b}^{y}=x,\text{}b>0,b\ne 1[/latex]
Note that the base b is always positive.
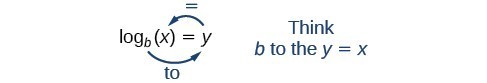
Because a logarithm is a function, it is most correctly written as [latex]{\mathrm{log}}_{b}\left(x\right)[/latex] using parentheses to denote function evaluation just as we would with [latex]f\left(x\right)[/latex]. However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written without parentheses as [latex]{\mathrm{log}}_{b}x[/latex]. Note that many calculators require parentheses around the x.
We can illustrate the notation of logarithms as follows:
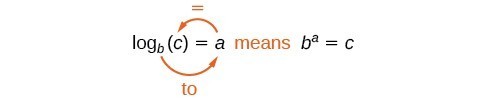
Note: Sometimes, you will see the natural logarithm [latex]ln[/latex] in place of [latex]log[/latex]. What is important to know is that the natural logarithm ([latex]ln[/latex]) is understood to have the number [latex]e[/latex] as its base. The value of [latex]e[/latex] is about 2.718.
How To: Given an equation in logarithmic form [latex]{\mathrm{log}}_{b}\left(x\right)=y[/latex], convert it to exponential form
- Examine the equation [latex]y={\mathrm{log}}_{b}x[/latex] and identify b, y, and x.
- Rewrite [latex]{\mathrm{log}}_{b}x=y[/latex] as [latex]{b}^{y}=x[/latex].
Example: Converting from Logarithmic Form to Exponential Form
Write the following logarithmic equations in exponential form.
- [latex]{\mathrm{log}}_{6}\left(\sqrt{6}\right)=\frac{1}{2}[/latex]
- [latex]{\mathrm{ln}}\left(9\right)=a[/latex]
Try It
Write the following logarithmic equations in exponential form.
- [latex]{\mathrm{log}}_{10}\left(1,000,000\right)=6[/latex]
- [latex]{\mathrm{log}}_{5}\left(25\right)=2[/latex]
Try It
Use the Power Property for Logarithms
A General Note: The Power Rule for Logarithms
The power rule for logarithms can be used to simplify the logarithm of a power by rewriting it as the product of the exponent times the logarithm of the base.
[latex]{\mathrm{log}}_{b}\left({M}^{n}\right)=n{\mathrm{log}}_{b}M[/latex]
Example: Expanding a Logarithm with Powers
Rewrite [latex]{\mathrm{log}}_{2}{x}^{5}[/latex].
Try It
Rewrite [latex]\mathrm{ln}{x}^{2}[/latex].
Example: Rewriting an Expression as a Power before Using the Power Rule
Rewrite [latex]{\mathrm{log}}_{3}\left(25\right)[/latex] using the power rule for logs.
Try It
Rewrite [latex]\mathrm{ln}\left(\frac{1}{{x}^{2}}\right)[/latex].
