Problem Set: Derivatives and the Shape of a Graph

1. If [latex]c[/latex] is a critical point of [latex]f(x)[/latex], when is there no local maximum or minimum at [latex]c[/latex]? Explain. 

2. For the function [latex]y=x^3[/latex], is [latex]x=0[/latex] both an inflection point and a local maximum/minimum?

3. For the function [latex]y=x^3[/latex], is [latex]x=0[/latex] an inflection point?

4. Is it possible for a point [latex]c[/latex] to be both an inflection point and a local extrema of a twice differentiable function?

5. Why do you need continuity for the first derivative test? Come up with an example.

6. Explain whether a concave-down function has to cross [latex]y=0[/latex] for some value of [latex]x[/latex].

7. Explain whether a polynomial of degree 2 can have an inflection point.

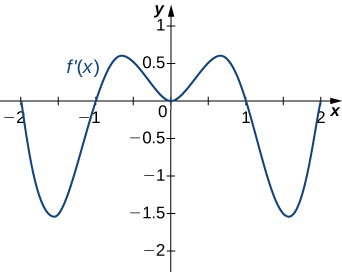
For the following exercises (8-12), analyze the graphs of [latex]f^{\prime}[/latex], then list all intervals where [latex]f[/latex] is increasing or decreasing.

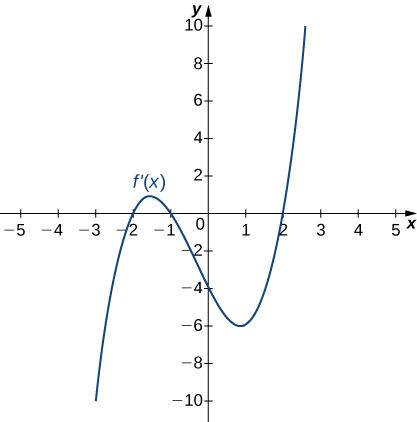
8. The function f’(x) is graphed. The function starts negative and crosses the x axis at (−2, 0). Then it continues increasing a little before decreasing and crossing the x axis at (−1, 0). It achieves a local minimum at (1, −6) before increasing and crossing the x axis at (2, 0).

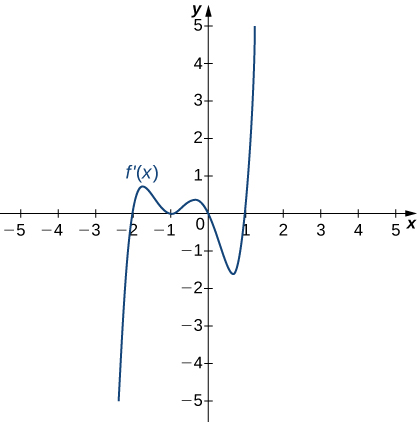
9. The function f’(x) is graphed. The function starts negative and crosses the x axis at (−2, 0). Then it continues increasing a little before decreasing and touching the x axis at (−1, 0). It then increases a little before decreasing and crossing the x axis at the origin. The function then decreases to a local minimum before increasing, crossing the x-axis at (1, 0), and continuing to increase.
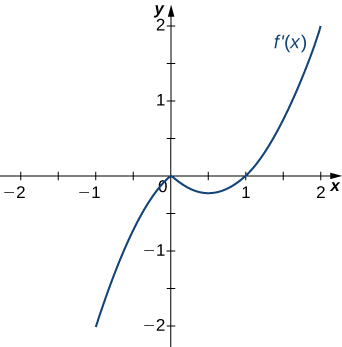
10. The function f’(x) is graphed. The function starts negative and touches the x axis at the origin. Then it decreases a little before increasing to cross the x axis at (1, 0) and continuing to increase.

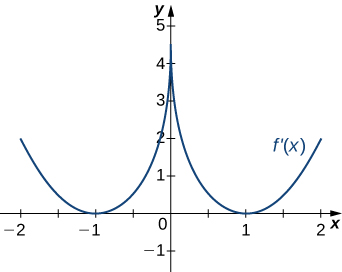
11. The function f’(x) is graphed. The function starts positive and decreases to touch the x axis at (−1, 0). Then it increases to (0, 4.5) before decreasing to touch the x axis at (1, 0). Then the function increases.
12. The function f’(x) is graphed. The function starts at (−2, 0), decreases to (−1.5, −1.5), increases to (−1, 0), and continues increasing before decreasing to the origin. Then the other side is symmetric: that is, the function increases and then decreases to pass through (1, 0). It continues decreasing to (1.5, −1.5), and then increase to (2, 0).

For the following exercises (13-17), analyze the graphs of [latex]f^{\prime}[/latex], then list

  1. all intervals where [latex]f[/latex] is increasing and decreasing and
  2. where the minima and maxima are located.
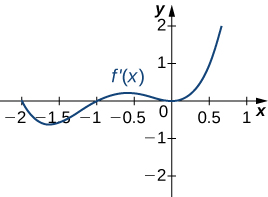
13. The function f’(x) is graphed. The function starts at (−2, 0), decreases for a little and then increases to (−1, 0), continues increasing before decreasing to the origin, at which point it increases.
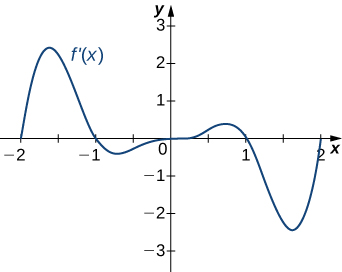
14. The function f’(x) is graphed. The function starts at (−2, 0), increases and then decreases to (−1, 0), decreases and then increases to an inflection point at the origin. Then the function increases and decreases to cross (1, 0). It continues decreasing and then increases to (2, 0).

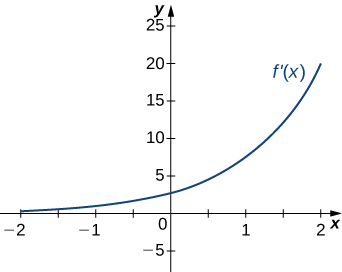
15. The function f’(x) is graphed from x = −2 to x = 2. It starts near zero at x = −2, but then increases rapidly and remains positive for the entire length of the graph.
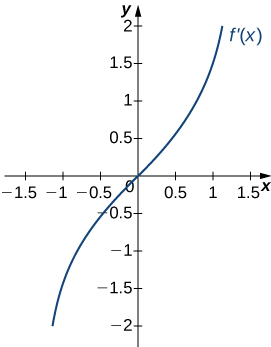
16. The function f’(x) is graphed. The function starts negative and crosses the x axis at the origin, which is an inflection point. Then it continues increasing.

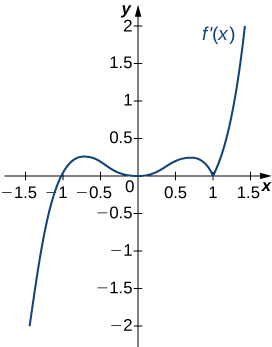
17. The function f’(x) is graphed. The function starts negative and crosses the x axis at (−1, 0). Then it continues increasing a little before decreasing and touching the x axis at the origin. It increases again and then decreases to (1, 0). Then it increases.

For the following exercises (18-22), analyze the graphs of [latex]f^{\prime}[/latex], then list all inflection points and intervals [latex]f[/latex] that are concave up and concave down.

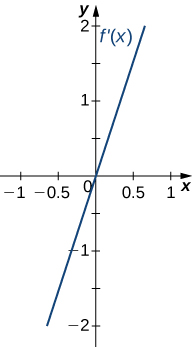
18. The function f’(x) is graphed. The function is linear and starts negative. It crosses the x axis at the origin.

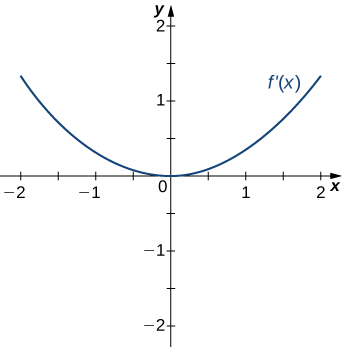
19. The function f’(x) is graphed. It is an upward-facing parabola with 0 as its local minimum.
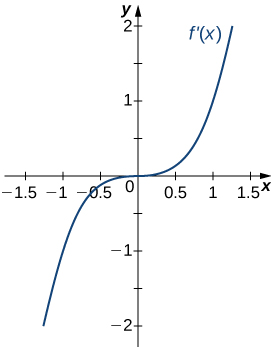
20. The function f’(x) is graphed. The function resembles the graph of x3: that is, it starts negative and crosses the x axis at the origin. Then it continues increasing.

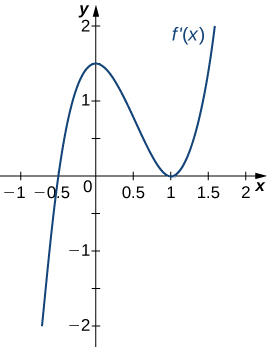
21. The function f’(x) is graphed. The function starts negative and crosses the x axis at (−0.5, 0). Then it continues increasing to (0, 1.5) before decreasing and touching the x axis at (1, 0). It then increases.
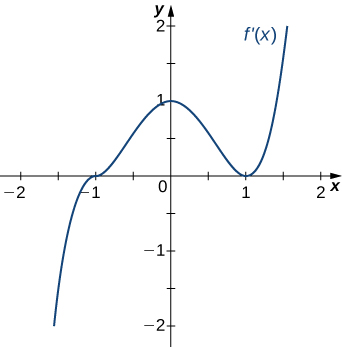
22. The function f’(x) is graphed. The function starts negative and crosses the x axis at (−1, 0). Then it continues increasing to a local maximum at (0, 1), at which point it decreases and touches the x axis at (1, 0). It then increases.

For the following exercises (23-27), draw a graph that satisfies the given specifications for the domain [latex]x=[-3,3][/latex]. The function does not have to be continuous or differentiable.

23. [latex]f(x)>0, \, f^{\prime}(x)>0[/latex] over [latex]x>1, \, -3

24. [latex]f^{\prime}(x)>0[/latex] over [latex]x>2, \, -3

25. [latex]f^{\prime \prime}(x)<0[/latex] over [latex]-10, \, -3

26. There is a local maximum at [latex]x=2[/latex], local minimum at [latex]x=1[/latex], and the graph is neither concave up nor concave down.

27. There are local maxima at [latex]x=\pm 1[/latex], the function is concave up for all [latex]x[/latex], and the function remains positive for all [latex]x[/latex].

For the following exercise, determine a. intervals where [latex]f[/latex] is concave up or concave down, and b. the inflection points of [latex]f[/latex].

30. [latex]f(x)=x^3-4x^2+x+2[/latex]

For the following exercises (31-37), determine

  1. intervals where [latex]f[/latex] is increasing or decreasing,
  2. local minima and maxima of [latex]f[/latex],
  3. intervals where [latex]f[/latex] is concave up and concave down, and
  4. the inflection points of [latex]f[/latex].

31. [latex]f(x)=x^2-6x[/latex]

32. [latex]f(x)=x^3-6x^2[/latex]

33. [latex]f(x)=x^4-6x^3[/latex]

34. [latex]f(x)=x^{11}-6x^{10}[/latex]

35. [latex]f(x)=x+x^2-x^3[/latex]

36. [latex]f(x)=x^2+x+1[/latex]

37. [latex]f(x)=x^3+x^4[/latex]

For the following exercises (38-47), determine

  1. intervals where [latex]f[/latex] is increasing or decreasing,
  2. local minima and maxima of [latex]f[/latex],
  3. intervals where [latex]f[/latex] is concave up and concave down, and
  4. the inflection points of [latex]f[/latex]. Sketch the curve, then use a calculator to compare your answer. If you cannot determine the exact answer analytically, use a calculator.

38. [T] [latex]f(x)= \sin (\pi x)- \cos (\pi x)[/latex] over [latex]x=[-1,1][/latex]

39. [T] [latex]f(x)=x + \sin (2x)[/latex] over [latex]x=\left[-\frac{\pi }{2},\frac{\pi }{2}\right][/latex]

40. [T] [latex]f(x)= \sin x+ \tan x[/latex] over [latex]\left(-\frac{\pi }{2},\frac{\pi }{2}\right)[/latex]

41. [T] [latex]f(x)=(x-2)^2 (x-4)^2[/latex]

42. [T] [latex]f(x)=\dfrac{1}{1-x}, \, x \ne 1[/latex]

43. [T] [latex]f(x)=\dfrac{\sin x}{x}[/latex] over [latex]x=[-2\pi ,0) \cup (0,2\pi][/latex]

44. [latex]f(x)= \sin x e^x[/latex] over [latex]x=[−\pi ,\pi][/latex]

45. [latex]f(x)=\ln x \sqrt{x}, \, x>0[/latex]

46. [latex]f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x}, \, x>0[/latex]

47. [latex]f(x)=\dfrac{e^x}{x}, \, x\ne 0[/latex]

For the following exercises (48-52), interpret the sentences in terms of [latex]f, \, f^{\prime}[/latex], and [latex]f^{\prime \prime}[/latex].

48. The population is growing more slowly. Here [latex]f[/latex] is the population.

49. A bike accelerates faster, but a car goes faster. Here [latex]f[/latex] represents the Bike’s position minus the Car’s position.

50. The airplane lands smoothly. Here [latex]f[/latex] is the plane’s altitude.

51. Stock prices are at their peak. Here [latex]f[/latex] is the stock price.

52. The economy is picking up speed. Here [latex]f[/latex] is a measure of the economy, such as GDP.

For the following exercises (53-57), consider a third-degree polynomial [latex]f(x)[/latex], which has the properties [latex]f^{\prime}(1)=0, \, f^{\prime}(3)=0[/latex]. Determine whether the following statements are true or false. Justify your answer.

53. [latex]f(x)=0[/latex] for some [latex]1 \le x \le 3[/latex]

54. [latex]f^{\prime \prime}(x)=0[/latex] for some [latex]1 \le x \le 3[/latex]

55. There is no absolute maximum at [latex]x=3[/latex]

56. If [latex]f(x)[/latex] has three roots, then it has 1 inflection point.

57. If [latex]f(x)[/latex] has one inflection point, then it has three real roots.