Problem Set: Inverse Functions

For the following exercises (1-6), use the horizontal line test to determine whether each of the given graphs is one-to-one.

1.
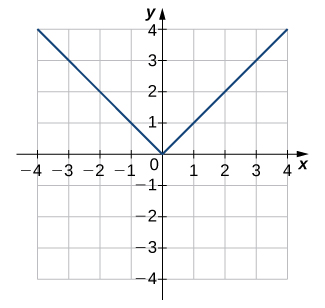
An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a function that decreases in a straight in until the origin, where it begins to increase in a straight line. The x intercept and y intercept are both at the origin.

2.
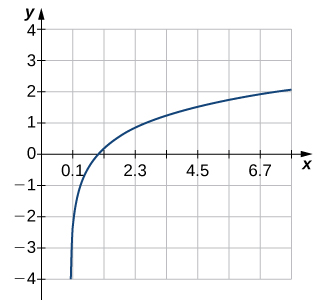
An image of a graph. The x axis runs from 0 to 7 and the y axis runs from -4 to 4. The graph is of a function that is always increasing. There is an approximate x intercept at the point (1, 0) and no y intercept shown.
3.
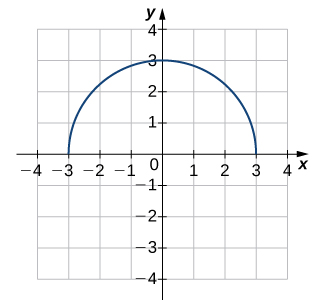
An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a function that resembles a semi-circle, the top half of a circle. The function starts at the point (-3, 0) and increases until the point (0, 3), where it begins decreasing until it ends at the point (3, 0). The x intercepts are at (-3, 0) and (3, 0). The y intercept is at (0, 3).

4.
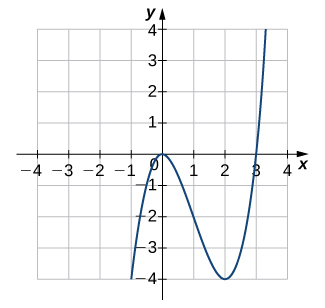
An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a curved function. The function increases until it hits the origin, then decreases until it hits the point (2, -4), where it begins to increase again. There are x intercepts at the origin and the point (3, 0). The y intercept is at the origin.
5.
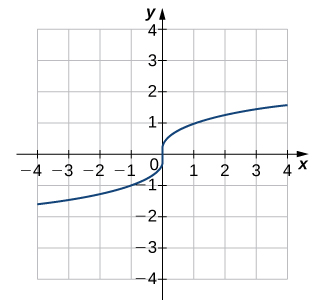
An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a curved function that is always increasing. The x intercept and y intercept are both at the origin.

6.
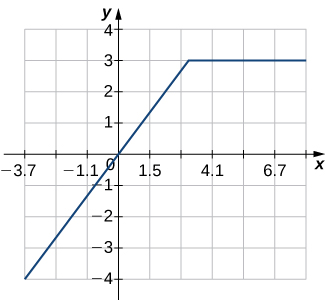
An image of a graph. The x axis runs from -4 to 7 and the y axis runs from -4 to 4. The graph is of a function that increases in a straight line until the approximate point (, 3). After this point, the function becomes a horizontal straight line. The x intercept and y intercept are both at the origin.

For the following exercises (7-12), (a) find the inverse function, and (b) find the domain and range of the inverse function.

7. [latex]f(x)=x^2-4, \, x \ge 0[/latex]

8. [latex]f(x)=\sqrt[3]{x-4}[/latex]

9. [latex]f(x)=x^3+1[/latex]

10. [latex]f(x)=(x-1)^2, \, x \le 1[/latex]

11. [latex]f(x)=\sqrt{x-1}[/latex]

12. [latex]f(x)=\dfrac{1}{x+2}[/latex]

For the following exercises (13-16), use the graph of [latex]f[/latex] to sketch the graph of its inverse function.

13.
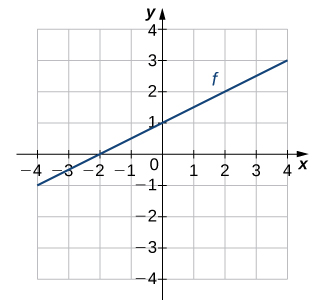
An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of an increasing straight line function labeled “f” that is always increasing. The x intercept is at (-2, 0) and y intercept are both at (0, 1).

14.
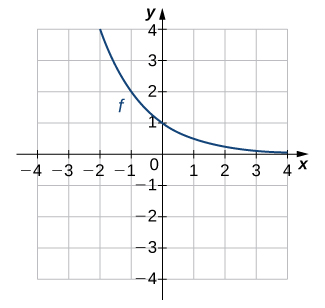
An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a curved decreasing function labeled “f”. As the function decreases, it gets approaches the x axis but never touches it. The function does not have an x intercept and the y intercept is (0, 1).
15.
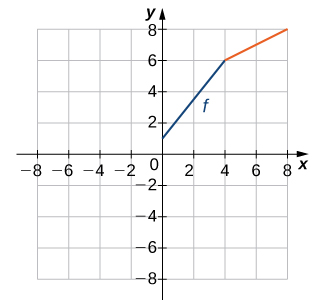
An image of a graph. The x axis runs from -8 to 8 and the y axis runs from -8 to 8. The graph is of an increasing straight line function labeled “f”. The function starts at the point (0, 1) and increases in straight line until the point (4, 6). After this point, the function continues to increase, but at a slower rate than before, as it approaches the point (8, 8). The function does not have an x intercept and the y intercept is (0, 1).

16.
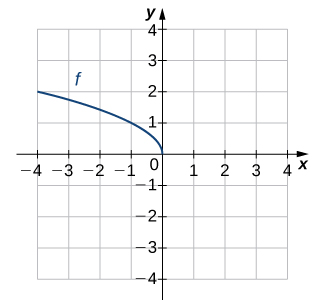
An image of a graph. The x axis runs from -4 to 4 and the y axis runs from -4 to 4. The graph is of a decreasing curved function labeled “f”, which ends at the origin, which is both the x intercept and y intercept. Another point on the function is (-4, 2).

For the following exercises (17-24), use composition to determine which pairs of functions are inverses.

17. [latex]f(x)=8x, \,\,\, g(x)=\dfrac{x}{8}[/latex]

18. [latex]f(x)=8x+3,\,\,\, g(x)=\dfrac{x-3}{8}[/latex]

19. [latex]f(x)=5x-7,\,\,\, g(x)=\dfrac{x+5}{7}[/latex]

20. [latex]f(x)=\dfrac{2}{3}x+2,\,\,\, g(x)=\frac{3}{2}x+3[/latex]

21. [latex]f(x)=\dfrac{1}{x-1}, \, x \ne 1,\,\,\, g(x)=\dfrac{1}{x}+1, \, x \ne 0[/latex]

22. [latex]f(x)=x^3+1,\,\,\, g(x)=(x-1)^{1/3}[/latex]

23. [latex]f(x)=x^2+2x+1, \, x \ge -1,\,\,\, g(x)=-1+\sqrt{x}, \, x \ge 0[/latex]

24. [latex]f(x)=\sqrt{4-x^2}, \, 0 \le x \le 2,\,\,\, g(x)=\sqrt{4-x^2}, \, 0 \le x \le 2[/latex]

For the following exercises (25-33), evaluate the functions. Give the exact value.

25. [latex]\tan^{-1}\left(\frac{\sqrt{3}}{3}\right)[/latex]

26. [latex]\cos^{-1}\left(-\frac{\sqrt{2}}{2}\right)[/latex]

27. [latex]\cot^{-1}(1)[/latex]

28. [latex]\sin^{-1}(-1)[/latex]

29. [latex]\cos^{-1}\left(\frac{\sqrt{3}}{2}\right)[/latex]

30. [latex]\cos (\tan^{-1}(\sqrt{3}))[/latex]

31. [latex]\sin (\cos^{-1}\left(\frac{\sqrt{2}}{2})\right)[/latex]

32. [latex]\sin^{-1}\left( \sin \left(\frac{\pi}{3}\right)\right)[/latex]

33. [latex]\tan^{-1}\left( \tan \left(-\frac{\pi}{6}\right)\right)[/latex]

34. The function [latex]C=T(F)=\left(\frac{5}{9}\right)(F-32)[/latex] converts degrees Fahrenheit to degrees Celsius.

  1. Find the inverse function [latex]F=T^{-1}(C)[/latex]
  2. What is the inverse function used for?

35. [T] The velocity [latex]V[/latex] (in centimeters per second) of blood in an artery at a distance [latex]x[/latex] cm from the center of the artery can be modeled by the function [latex]V=f(x)=500(0.04-x^2)[/latex] for [latex]0 \le x \le 0.2[/latex].

  1. Find [latex]x=f^{-1}(V)[/latex].
  2. Interpret what the inverse function is used for.
  3. Find the distance from the center of an artery with a velocity of 15 cm/sec, 10 cm/sec, and 5 cm/sec.

36. A function that converts dress sizes in the United States to those in Europe is given by [latex]D(x)=2x+24[/latex].

  1. Find the European dress sizes that correspond to sizes 6, 8, 10, and 12 in the United States.
  2. Find the function that converts European dress sizes to U.S. dress sizes.
  3. Use part (b) to find the dress sizes in the United States that correspond to 46, 52, 62, and 70.

37. [T] The cost to remove a toxin from a lake is modeled by the function

[latex]C(p)=\dfrac{75p}{(85-p)}[/latex],

where [latex]C[/latex] is the cost (in thousands of dollars) and [latex]p[/latex] is the amount of toxin in a small lake (measured in parts per billion [ppb]). This model is valid only when the amount of toxin is less than 85 ppb.

  1. Find the cost to remove 25 ppb, 40 ppb, and 50 ppb of the toxin from the lake.
  2. Find the inverse function.
  3. Use part (b) to determine how much of the toxin is removed for $50,000.

38. [T] A race car is accelerating at a velocity given by

[latex]v(t)=\frac{25}{4}t+54[/latex],

where [latex]v[/latex] is the velocity (in feet per second) at time [latex]t[/latex].

  1. Find the velocity of the car at 10 sec.
  2. Find the inverse function.
  3. Use part (b) to determine how long it takes for the car to reach a speed of 150 ft/sec.

39. [T] An airplane’s Mach number [latex]M[/latex] is the ratio of its speed to the speed of sound. When a plane is flying at a constant altitude, then its Mach angle is given by [latex]\mu =2\sin^{-1}\left(\frac{1}{M}\right)[/latex].

Find the Mach angle (to the nearest degree) for the following Mach numbers.

An image of a birds eye view of an airplane. Directly in front of the airplane is a sideways “V” shape, with the airplane flying directly into the opening of the “V” shape. The “V” shape is labeled “mach wave”. There are two arrows with labels. The first arrow points from the nose of the airplane to the corner of the “V” shape. This arrow has the label “velocity = v”. The second arrow points diagonally from the nose of the airplane to the edge of the upper portion of the “V” shape. This arrow has the label “speed of sound = a”. Between these two arrows is an angle labeled “Mach angle”. There is also text in the image that reads “mach = M > 1.0”.

  1. [latex]M =1.4[/latex]
  2. [latex]M =2.8[/latex]
  3. [latex]M =4.3[/latex]

40. [T] Using [latex]\mu =2\sin^{-1}\left(\frac{1}{M}\right)[/latex], find the Mach number [latex]M[/latex] for the following angles.

  1. [latex]\mu =\dfrac{\pi}{6}[/latex]
  2. [latex]\mu =\dfrac{2\pi}{7}[/latex]
  3. [latex]\mu =\dfrac{3\pi}{8}[/latex]

41. [T] The temperature (in degrees Celsius) of a city in the northern United States can be modeled by the function

[latex]T(x)=5+18 \sin\left[\frac{\pi}{6}(x-4.6)\right][/latex],

where [latex]x[/latex] is time in months and [latex]x=1.00[/latex] corresponds to January 1. Determine the month and day when the temperature is [latex]21^{\circ}[/latex] C.

42. [T] The depth (in feet) of water at a dock changes with the rise and fall of tides. It is modeled by the function

[latex]D(t)=5 \sin \left(\frac{\pi}{6}t-\frac{7\pi}{6}\right)+8[/latex],

where [latex]t[/latex] is the number of hours after midnight. Determine the first time after midnight when the depth is 11.75 ft.

43. [T] An object moving in simple harmonic motion is modeled by the function

[latex]s(t)=-6 \cos \left(\frac{\pi t}{2}\right)[/latex],

where [latex]s[/latex] is measured in inches and [latex]t[/latex] is measured in seconds. Determine the first time when the distance moved is 4.5 in.

44. [T] A local art gallery has a portrait 3 ft in height that is hung 2.5 ft above the eye level of an average person. The viewing angle [latex]\theta[/latex] can be modeled by the function

[latex]\theta =\tan^{-1}\left(\dfrac{5.5}{x}\right)-\tan^{-1}\left(\dfrac{2.5}{x}\right)[/latex],

where [latex]x[/latex] is the distance (in feet) from the portrait. Find the viewing angle when a person is 4 ft from the portrait.

45. [T] Use a calculator to evaluate [latex]\tan^{-1}( \tan (2.1))[/latex] and [latex]\cos^{-1}( \cos (2.1))[/latex]. Explain the results of each.

46. [T] Use a calculator to evaluate [latex]\sin (\sin^{-1}(-2))[/latex] and [latex]\tan (\tan^{-1}(-2))[/latex]. Explain the results of each.