Problem Set: The Derivative as a Function

For the following exercises (1-10), use the definition of a derivative to find [latex]f^{\prime}(x)[/latex].

1. [latex]f(x)=6[/latex]

2. [latex]f(x)=2-3x[/latex]

3. [latex]f(x)=\dfrac{2x}{7}+1[/latex]

4. [latex]f(x)=4x^2[/latex]

5. [latex]f(x)=5x-x^2[/latex]

6. [latex]f(x)=\sqrt{2x}[/latex]

7. [latex]f(x)=\sqrt{x-6}[/latex]

8. [latex]f(x)=\dfrac{9}{x}[/latex]

9. [latex]f(x)=x+\dfrac{1}{x}[/latex]

10. [latex]f(x)=\dfrac{1}{\sqrt{x}}[/latex]

For the following exercises (11-14), use the graph of [latex]y=f(x)[/latex] to sketch the graph of its derivative [latex]f^{\prime}(x)[/latex].

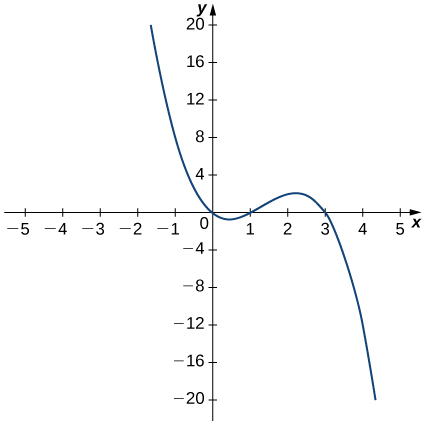
11. The function f(x) starts at (−2, 20) and decreases to pass through the origin and achieve a local minimum at roughly (0.5, −1). Then, it increases and passes through (1, 0) and achieves a local maximum at (2.25, 2) before decreasing again through (3, 0) to (4, −20).
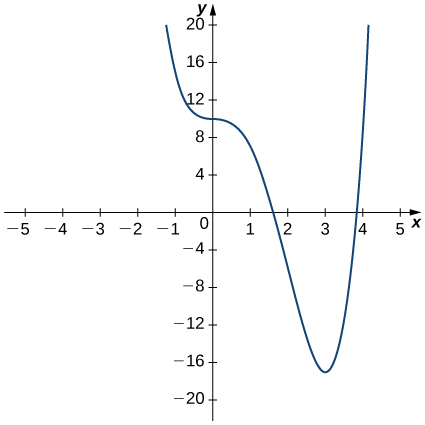
12. The function f(x) starts at (−1.5, 20) and decreases to pass through (0, 10), where it appears to have a derivative of 0. Then it further decreases, passing through (1.7, 0) and achieving a minimum at (3, −17), at which point it increases rapidly through (3.8, 0) to (4, 20).

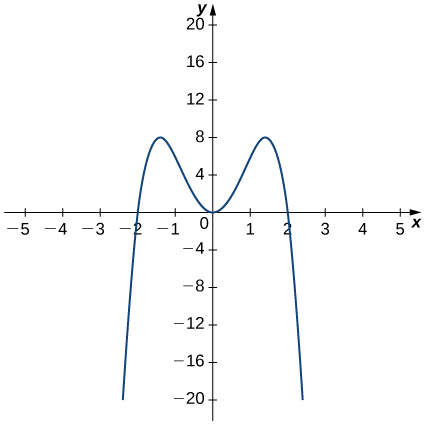
13. The function f(x) starts at (−2.25, −20) and increases rapidly to pass through (−2, 0) before achieving a local maximum at (−1.4, 8). Then the function decreases to the origin. The graph is symmetric about the y-axis, so the graph increases to (1.4, 8) before decreasing through (2, 0) and heading on down to (2.25, −20).
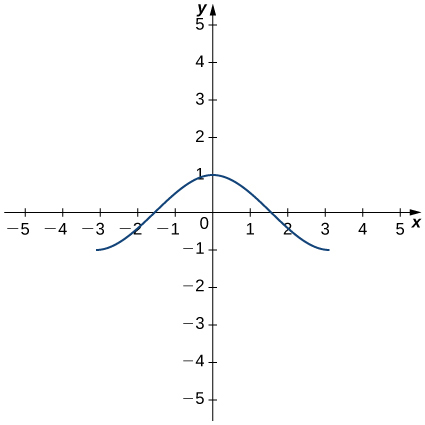
14. The function f(x) starts at (−3, −1) and increases to pass through (−1.5, 0) and achieve a local minimum at (1, 0). Then, it decreases and passes through (1.5, 0) and continues decreasing to (3, −1).

For the following exercises (15-20), the given limit represents the derivative of a function [latex]y=f(x)[/latex] at [latex]x=a[/latex]. Find [latex]f(x)[/latex] and [latex]a[/latex].

15. [latex]\underset{h\to 0}{\lim}\dfrac{(1+h)^{\frac{2}{3}}-1}{h}[/latex]

16. [latex]\underset{h\to 0}{\lim}\dfrac{[3(2+h)^2+2]-14}{h}[/latex]

17. [latex]\underset{h\to 0}{\lim}\dfrac{\cos(\pi+h)+1}{h}[/latex]

18. [latex]\underset{h\to 0}{\lim}\dfrac{(2+h)^4-16}{h}[/latex]

19. [latex]\underset{h\to 0}{\lim}\dfrac{\left[2(3+h)^2-(3+h)\right]-15}{h}[/latex]

20. [latex]\underset{h\to 0}{\lim}\dfrac{e^h-1}{h}[/latex]

For the following functions (21-24),

  1. sketch the graph and
  2. use the definition of a derivative to show that the function is not differentiable at [latex]x=1[/latex].

21. [latex]f(x)=\begin{cases} 2\sqrt{x} & \text{ if } \, 0 \le x \le 1 \\ 3x-1 & \text{ if } \, x>1 \end{cases}[/latex]

22. [latex]f(x)=\begin{cases} 3 & \text{ if } \, x<1 \\ 3x & \text{ if } \, x \ge 1 \end{cases}[/latex]

23. [latex]f(x)=\begin{cases} -x^2+2 & \text{ if } \, x \le 1 \\ x & \text{ if } \, x>1 \end{cases}[/latex]

24. [latex]f(x)=\begin{cases} 2x & \text{ if } x \le 1 \\ \dfrac{2}{x} & \text{ if } \, x>1 \end{cases}[/latex]

For the following graphs (25-27),

  1. determine for which values of [latex]x=a[/latex] the [latex]\underset{x\to a}{\lim}f(x)[/latex] exists but [latex]f[/latex] is not continuous at [latex]x=a[/latex], and
  2. determine for which values of [latex]x=a[/latex] the function is continuous but not differentiable at [latex]x=a[/latex].
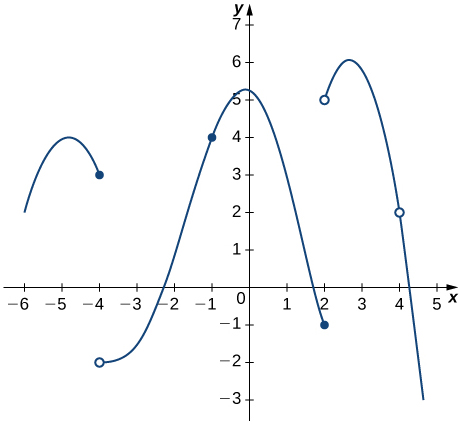
25. The function starts at (−6, 2) and increases to a maximum at (−5.3, 4) before stopping at (−4, 3) inclusive. Then it starts again at (−4, −2) before increasing slowly through (−2.25, 0), passing through (−1, 4), hitting a local maximum at (−0.1, 5.3) and decreasing to (2, −1) inclusive. Then it starts again at (2, 5), increases to (2.6, 6), and then decreases to (4.5, −3), with a discontinuity at (4, 2).
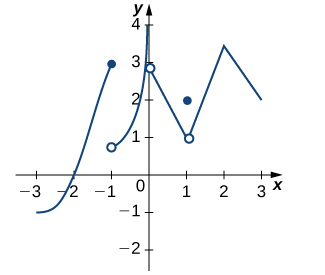
26. The function starts at (−3, −1) and increases to and stops at a local maximum at (−1, 3) inclusive. Then it starts again at (−1, 1) before increasing quickly to and stopping at a local maximum (0, 4) inclusive. Then it starts again at (0, 3) and decreases linearly to (1, 1), at which point there is a discontinuity and the value of this function at x = 1 is 2. The function continues from (1, 1) and increases linearly to (2, 3.5) before decreasing linearly to (3, 2).

27. Use the graph to evaluate a. [latex]f^{\prime}(-0.5)[/latex], b. [latex]f^{\prime}(0)[/latex], c. [latex]f^{\prime}(1)[/latex], d. [latex]f^{\prime}(2)[/latex], and e. [latex]f^{\prime}(3)[/latex], if they exist.

The function starts at (−3, 0) and increases linearly to a local maximum at (0, 3). Then it decreases linearly to (2, 1), at which point it increases linearly to (4, 5).

For the following functions (28-30), use [latex]f''(x)=\underset{h\to 0}{\lim}\dfrac{f^{\prime}(x+h)-f^{\prime}(x)}{h}[/latex] to find [latex]f''(x)[/latex].

28. [latex]f(x)=2-3x[/latex]

29. [latex]f(x)=4x^2[/latex]

30. [latex]f(x)=x+\dfrac{1}{x}[/latex]

For the following exercises (31-36), use a calculator to graph [latex]f(x)[/latex]. Determine the function [latex]f^{\prime}(x)[/latex], then use a calculator to graph [latex]f^{\prime}(x)[/latex].

31. [T] [latex]f(x)=-\dfrac{5}{x}[/latex]

32. [T] [latex]f(x)=3x^2+2x+4[/latex]

33. [T] [latex]f(x)=\sqrt{x}+3x[/latex]

34. [T] [latex]f(x)=\dfrac{1}{\sqrt{2x}}[/latex]

35. [T] [latex]f(x)=1+x+\dfrac{1}{x}[/latex]

36. [T] [latex]f(x)=x^3+1[/latex]

For the following exercises (37-42), describe what the two expressions represent in terms of each of the given situations. Be sure to include units.

  1. [latex]\dfrac{f(x+h)-f(x)}{h}[/latex]
  2. [latex]f^{\prime}(x)=\underset{h\to 0}{\lim}\dfrac{f(x+h)-f(x)}{h}[/latex]

37. [latex]P(x)[/latex] denotes the population of a city at time [latex]x[/latex] in years.

38. [latex]C(x)[/latex] denotes the total amount of money (in thousands of dollars) spent on concessions by [latex]x[/latex] customers at an amusement park.

39. [latex]R(x)[/latex] denotes the total cost (in thousands of dollars) of manufacturing [latex]x[/latex] clock radios.

40. [latex]g(x)[/latex] denotes the grade (in percentage points) received on a test, given [latex]x[/latex] hours of studying.

41. [latex]B(x)[/latex] denotes the cost (in dollars) of a sociology textbook at university bookstores in the United States in [latex]x[/latex] years since 1990.

42. [latex]p(x)[/latex] denotes atmospheric pressure at an altitude of [latex]x[/latex] feet.

43. Sketch the graph of a function [latex]y=f(x)[/latex] with all of the following properties:

  1. [latex]f^{\prime}(x)>0[/latex] for [latex]-2\le x<1[/latex]
  2. [latex]f^{\prime}(2)=0[/latex]
  3. [latex]f^{\prime}(x)>0[/latex] for [latex]x>2[/latex]
  4. [latex]f(2)=2[/latex] and [latex]f(0)=1[/latex]
  5. [latex]\underset{x\to −\infty}{\lim}f(x)=0[/latex] and [latex]\underset{x\to \infty}{\lim}f(x)=\infty[/latex]
  6. [latex]f^{\prime}(1)[/latex] does not exist.

44. Suppose temperature [latex]T[/latex] in degrees Fahrenheit at a height [latex]x[/latex] in feet above the ground is given by [latex]y=T(x)[/latex].

  1. Give a physical interpretation, with units, of [latex]T^{\prime}(x)[/latex].
  2. If we know that [latex]{T}^{\prime }(1000)=-0.1,[/latex] explain the physical meaning.

45. Suppose the total profit of a company is [latex]y=P(x)[/latex] thousand dollars when [latex]x[/latex] units of an item are sold.

  1. What does [latex]\dfrac{P(b)-P(a)}{b-a}[/latex] for [latex]0
  2. What does [latex]P^{\prime}(x)[/latex] measure, and what are the units?
  3. Suppose that [latex]P^{\prime}(30)=5[/latex]. What is the approximate change in profit if the number of items sold increases from 30 to 31?

46. The graph in the following figure models the number of people [latex]N(t)[/latex] who have come down with the flu [latex]t[/latex] weeks after its initial outbreak in a town with a population of 50,000 citizens.

  1. Describe what [latex]N^{\prime}(t)[/latex] represents and how it behaves as [latex]t[/latex] increases.
  2. What does the derivative tell us about how this town is affected by the flu outbreak?

The function starts at (0, 3000) and increases quickly to an asymptote at y = 50000.

For the following exercises, use the following table, which shows the height [latex]h[/latex] of the Saturn V rocket for the Apollo 11 mission [latex]t[/latex] seconds after launch.

Time (seconds) Height (meters)
0 0
1 2
2 4
3 13
4 25
5 32

47. What is the physical meaning of [latex]h^{\prime}(t)[/latex]? What are the units?

48. [T] Construct a table of values for [latex]h^{\prime}(t)[/latex] and graph both [latex]h(t)[/latex] and [latex]h^{\prime}(t)[/latex] on the same graph. (Hint: for interior points, estimate both the left limit and right limit and average them. An interior point of an interval [latex]I[/latex] is an element of [latex]I[/latex] which is not an endpoint of [latex]I[/latex].)

49. [T] The best linear fit to the data is given by [latex]H(t)=7.229t-4.905[/latex], where [latex]H[/latex] is the height of the rocket (in meters) and [latex]t[/latex] is the time elapsed since takeoff. From this equation, determine [latex]H^{\prime}(t)[/latex]. Graph [latex]H(t)[/latex] with the given data and, on a separate coordinate plane, graph [latex]H^{\prime}(t)[/latex].

50. [T] The best quadratic fit to the data is given by [latex]G(t)=1.429t^2+0.0857t-0.1429[/latex], where [latex]G[/latex] is the height of the rocket (in meters) and [latex]t[/latex] is the time elapsed since takeoff. From this equation, determine [latex]G^{\prime}(t)[/latex]. Graph [latex]G(t)[/latex] with the given data and, on a separate coordinate plane, graph [latex]G^{\prime}(t)[/latex].

51. [T] The best cubic fit to the data is given by [latex]F(t)=0.2037t^3+2.956t^2-2.705t+0.4683[/latex], where [latex]F[/latex] is the height of the rocket (in m) and [latex]t[/latex] is the time elapsed since take off. From this equation, determine [latex]F^{\prime}(t)[/latex]. Graph [latex]F(t)[/latex] with the given data and, on a separate coordinate plane, graph [latex]F^{\prime}(t)[/latex]. Does the linear, quadratic, or cubic function fit the data best?

52. Using the best linear, quadratic, and cubic fits to the data, determine what [latex]H''(t), \, G''(t)[/latex], and [latex]F''(t)[/latex] are. What are the physical meanings of [latex]H''(t), \, G''(t)[/latex], and [latex]F''(t)[/latex], and what are their units?