Problem Set: The Limit Laws

In the following exercises (1-4), use the limit laws to evaluate each limit. Justify each step by indicating the appropriate limit law(s).

1. [latex]\underset{x\to 0}{\lim}(4x^2-2x+3)[/latex]

2. [latex]\underset{x\to 1}{\lim}\frac{x^3+3x^2+5}{4-7x}[/latex]

3. [latex]\underset{x\to -2}{\lim}\sqrt{x^2-6x+3}[/latex]

4. [latex]\underset{x\to -1}{\lim}(9x+1)^2[/latex]

In the following exercises (5-10), use direct substitution to evaluate each limit.

5. [latex]\underset{x\to 7}{\lim}x^2[/latex]

6. [latex]\underset{x\to -2}{\lim}(4x^2-1)[/latex]

7. [latex]\underset{x\to 0}{\lim}\dfrac{1}{1+ \sin x}[/latex]

8. [latex]\underset{x\to 2}{\lim}e^{2x-x^2}[/latex]

9. [latex]\underset{x\to 1}{\lim}\dfrac{2-7x}{x+6}[/latex]

10. [latex]\underset{x\to 3}{\lim}\ln e^{3x}[/latex]

In the following exercises (11-20), use direct substitution to show that each limit leads to the indeterminate form [latex]\frac{0}{0}[/latex]. Then, evaluate the limit.

11. [latex]\underset{x\to 4}{\lim}\dfrac{x^2-16}{x-4}[/latex]

12. [latex]\underset{x\to 2}{\lim}\dfrac{x-2}{x^2-2x}[/latex]

13. [latex]\underset{x\to 6}{\lim}\dfrac{3x-18}{2x-12}[/latex]

14. [latex]\underset{h\to 0}{\lim}\dfrac{(1+h)^2-1}{h}[/latex]

15. [latex]\underset{t\to 9}{\lim}\dfrac{t-9}{\sqrt{t}-3}[/latex]

16. [latex]\underset{h\to 0}{\lim}\dfrac{\frac{1}{a+h}-\frac{1}{a}}{h}[/latex], where [latex]a[/latex] is a real-valued constant

17. [latex]\underset{\theta \to \pi}{\lim}\dfrac{\sin \theta}{\tan \theta}[/latex]

18. [latex]\underset{x\to 1}{\lim}\dfrac{x^3-1}{x^2-1}[/latex]

19. [latex]\underset{x\to 1/2}{\lim}\dfrac{2x^2+3x-2}{2x-1}[/latex]

20. [latex]\underset{x\to -3}{\lim}\dfrac{\sqrt{x+4}-1}{x+3}[/latex]

In the following exercises (21-24), use direct substitution to obtain an undefined expression. Then, use the method of (Figure) to simplify the function to help determine the limit.

21. [latex]\underset{x\to -2^-}{\lim}\dfrac{2x^2+7x-4}{x^2+x-2}[/latex]

22. [latex]\underset{x\to -2^+}{\lim}\dfrac{2x^2+7x-4}{x^2+x-2}[/latex]

23. [latex]\underset{x\to 1^-}{\lim}\dfrac{2x^2+7x-4}{x^2+x-2}[/latex]

24. [latex]\underset{x\to 1^+}{\lim}\dfrac{2x^2+7x-4}{x^2+x-2}[/latex]

In the following exercises (25-32), assume that [latex]\underset{x\to 6}{\lim}f(x)=4, \, \underset{x\to 6}{\lim}g(x)=9[/latex], and [latex]\underset{x\to 6}{\lim}h(x)=6[/latex]. Use these three facts and the limit laws to evaluate each limit.

25. [latex]\underset{x\to 6}{\lim}2f(x)g(x)[/latex]

26. [latex]\underset{x\to 6}{\lim}\dfrac{g(x)-1}{f(x)}[/latex]

27. [latex]\underset{x\to 6}{\lim}(f(x)+\frac{1}{3}g(x))[/latex]

28. [latex]\underset{x\to 6}{\lim}\dfrac{(h(x))^3}{2}[/latex]

29. [latex]\underset{x\to 6}{\lim}\sqrt{g(x)-f(x)}[/latex]

30. [latex]\underset{x\to 6}{\lim}x \cdot h(x)[/latex]

31. [latex]\underset{x\to 6}{\lim}[(x+1)\cdot f(x)][/latex]

32. [latex]\underset{x\to 6}{\lim}(f(x)\cdot g(x)-h(x))[/latex]

In the following exercises (33-35), use a calculator to draw the graph of each piecewise-defined function and study the graph to evaluate the given limits.

33. [T] [latex]f(x)=\begin{cases} x^2, & x \le 3 \\ x+4, & x > 3 \end{cases}[/latex]

  1. [latex]\underset{x\to 3^-}{\lim}f(x)[/latex]
  2. [latex]\underset{x\to 3^+}{\lim}f(x)[/latex]

34. [T] [latex]g(x)=\begin{cases} x^3 - 1, & x \le 0 \\ 1, & x > 0 \end{cases}[/latex]

  1. [latex]\underset{x\to 0^-}{\lim}g(x)[/latex]
  2. [latex]\underset{x\to 0^+}{\lim}g(x)[/latex]

35. [T] [latex]h(x)=\begin{cases} x^2-2x+1, & x < 2 \\ 3 - x, & x \ge 2 \end{cases}[/latex]

    1. [latex]\underset{x\to 2^-}{\lim}h(x)[/latex]
    2. [latex]\underset{x\to 2^+}{\lim}h(x)[/latex]

In the following exercises (36-43), use the graphs below and the limit laws to evaluate each limit.

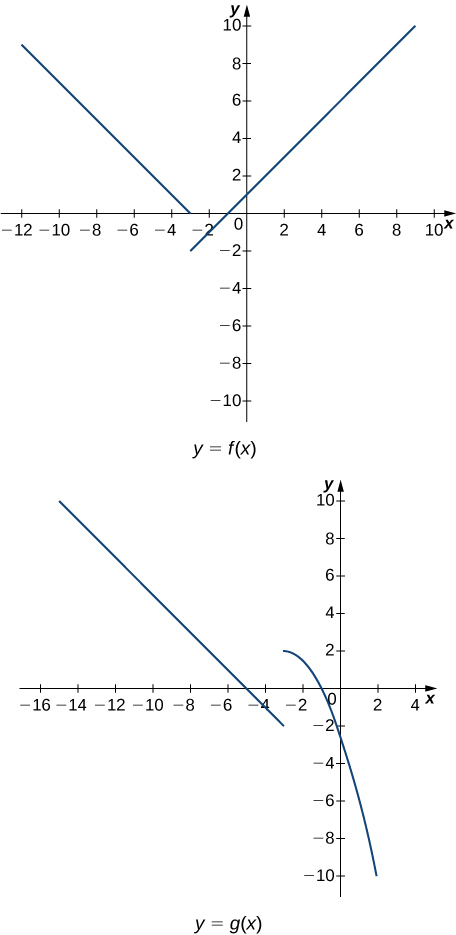
Two graphs of piecewise functions. The upper is f(x), which has two linear segments. The first is a line with negative slope existing for x < -3. It goes toward the point (-3,0) at x= -3. The next has increasing slope and goes to the point (-3,-2) at x=-3. It exists for x > -3. Other key points are (0, 1), (-5,2), (1,2), (-7, 4), and (-9,6). The lower piecewise function has a linear segment and a curved segment. The linear segment exists for x < -3 and has decreasing slope. It goes to (-3,-2) at x=-3. The curved segment appears to be the right half of a downward opening parabola. It goes to the vertex point (-3,2) at x=-3. It crosses the y axis a little below y=-2. Other key points are (0, -7/3), (-5,0), (1,-5), (-7, 2), and (-9, 4).

36. [latex]\underset{x\to -3^+}{\lim}(f(x)+g(x))[/latex]

37. [latex]\underset{x\to -3^-}{\lim}(f(x)-3g(x))[/latex]

38. [latex]\underset{x\to 0}{\lim}\dfrac{f(x)g(x)}{3}[/latex]

39. [latex]\underset{x\to -5}{\lim}\dfrac{2+g(x)}{f(x)}[/latex]

40. [latex]\underset{x\to 1}{\lim}(f(x))^2[/latex]

41. [latex]\underset{x\to 1}{\lim}\sqrt[3]{f(x)-g(x)}[/latex]

42. [latex]\underset{x\to -7}{\lim}(x \cdot g(x))[/latex]

43. [latex]\underset{x\to -9}{\lim}[xf(x)+2g(x)][/latex]

For the following problems (44-46), evaluate the limit using the Squeeze Theorem. Use a calculator to graph the functions [latex]f(x), \, g(x)[/latex], and [latex]h(x)[/latex] when possible.

44. [T] True or False? If [latex]2x-1\le g(x)\le x^2-2x+3[/latex], then [latex]\underset{x\to 2}{\lim}g(x)=0[/latex].

45. [T] [latex]\underset{\theta \to 0}{\lim}\theta^2 \cos\left(\frac{1}{\theta}\right)[/latex]

46. [latex]\underset{x\to 0}{\lim}f(x)[/latex], where [latex]f(x)=\begin{cases} 0, & x \, \text{rational} \\ x^2, & x \, \text{irrational} \end{cases}[/latex]

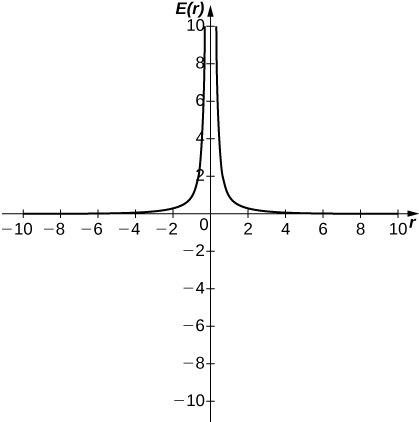
47. [T] In physics, the magnitude of an electric field generated by a point charge at a distance [latex]r[/latex] in vacuum is governed by Coulomb’s law: [latex]E(r)=\large \frac{q}{4\pi \varepsilon_0 r^2}[/latex], where [latex]E[/latex] represents the magnitude of the electric field, [latex]q[/latex] is the charge of the particle, [latex]r[/latex] is the distance between the particle and where the strength of the field is measured, and [latex]\large \frac{1}{4\pi \varepsilon_0}[/latex] is Coulomb’s constant: [latex]8.988 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2[/latex].

  1. Use a graphing calculator to graph [latex]E(r)[/latex] given that the charge of the particle is [latex]q=10^{-10}[/latex].
  2. Evaluate [latex]\underset{r\to 0^+}{\lim}E(r)[/latex]. What is the physical meaning of this quantity? Is it physically relevant? Why are you evaluating from the right?

48. [T] The density of an object is given by its mass divided by its volume: [latex]\rho =\dfrac{m}{V}[/latex].

  1. Use a calculator to plot the volume as a function of density [latex](V=\frac{m}{\rho})[/latex], assuming you are examining something of mass 8 kg ([latex]m=8[/latex]).
  2. Evaluate [latex]\underset{\rho \to 0^+}{\lim}V(\rho)[/latex] and explain the physical meaning.