Problem Set: The Limit of a Function

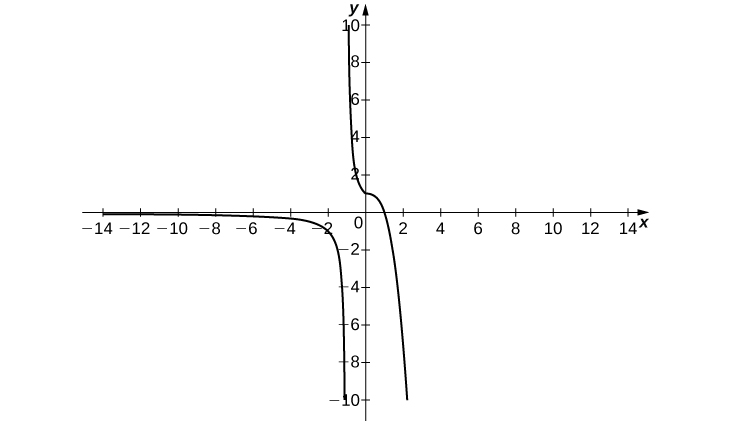
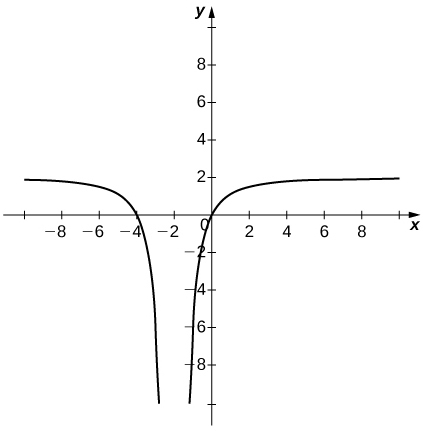
For the following exercises (1-2), consider the function [latex]f(x)=\dfrac{x^2-1}{|x-1|}[/latex].

1. [T] Complete the following table for the function. Round your solutions to four decimal places.

[latex]x[/latex] [latex]f(x)[/latex] [latex]x[/latex] [latex]f(x)[/latex]
0.9 a. 1.1 e.
0.99 b. 1.01 f.
0.999 c. 1.001 g.
0.9999 d. 1.0001 h.

2. What do your results in the preceding exercise indicate about the two-sided limit [latex]\underset{x\to 1}{\lim}f(x)[/latex]? Explain your response.

For the following exercises (3-5), consider the function [latex]f(x)=(1+x)^{1/x}[/latex].

3. [T] Make a table showing the values of [latex]f[/latex] for [latex]x=-0.01, \, -0.001, \, -0.0001, \, -0.00001[/latex] and for [latex]x=0.01, \, 0.001, \, 0.0001, \, 0.00001[/latex]. Round your solutions to five decimal places.

[latex]x[/latex] [latex]f(x)[/latex] [latex]x[/latex] [latex]f(x)[/latex]
−0.01 a. 0.01 e.
−0.001 b. 0.001 f.
−0.0001 c. 0.0001 g.
−0.00001 d. 0.00001 h.

4. What does the table of values in the preceding exercise indicate about the function [latex]f(x)=(1+x)^{1/x}[/latex]?

5. To which mathematical constant does the limit in the preceding exercise appear to be getting closer?

In the following exercises (6-8), use the given values of [latex]x[/latex] to set up a table to evaluate the limits. Round your solutions to eight decimal places.

6. [T] [latex]\underset{x\to 0}{\lim}\dfrac{\sin 2x}{x}; \, x = \pm 0.1, \, \pm 0.01, \, \pm 0.001, \, \pm 0.0001[/latex]

[latex]x[/latex] [latex]\frac{\sin 2x}{x}[/latex] [latex]x[/latex] [latex]\frac{\sin 2x}{x}[/latex]
−0.1 a. 0.1 e.
−0.01 b. 0.01 f.
−0.001 c. 0.001 g.
−0.0001 d. 0.0001 h.

7. [T] [latex]\underset{x\to 0}{\lim}\dfrac{\sin 3x}{x}; \, x = \pm 0.1, \, \pm 0.01, \, \pm 0.001, \, \pm 0.0001[/latex]

X [latex]\frac{\sin 3x}{x}[/latex] [latex]x[/latex] [latex]\frac{\sin 3x}{x}[/latex]
−0.1 a. 0.1 e.
−0.01 b. 0.01 f.
−0.001 c. 0.001 g.
−0.0001 d. 0.0001 h.

8. Use the preceding two exercises to conjecture (guess) the value of the following limit: [latex]\underset{x\to 0}{\lim}\dfrac{\sin ax}{x}[/latex] for [latex]a[/latex], a positive real value.

In the following exercises (9-14), set up a table of values to find the indicated limit. Round to eight digits.

9. [T] [latex]\underset{x\to 2}{\lim}\dfrac{x^2-4}{x^2+x-6}[/latex]

[latex]x[/latex] [latex]\frac{x^2-4}{x^2+x-6}[/latex] [latex]x[/latex] [latex]\frac{x^2-4}{x^2+x-6}[/latex]
1.9 a. 2.1 e.
1.99 b. 2.01 f.
1.999 c. 2.001 g.
1.9999 d. 2.0001 h.

10. [T] [latex]\underset{x\to 1}{\lim}(1-2x)[/latex]

[latex]x[/latex] [latex]1-2x[/latex] [latex]x[/latex] [latex]1-2x[/latex]
0.9 a. 1.1 e.
0.99 b. 1.01 f.
0.999 c. 1.001 g.
0.9999 d. 1.0001 h.

11. [T] [latex]\underset{x\to 0}{\lim}\dfrac{5}{1-e^{1/x}}[/latex]

[latex]x[/latex] [latex]\frac{5}{1-e^{1/x}}[/latex] [latex]x[/latex] [latex]\frac{5}{1-e^{1/x}}[/latex]
−0.1 a. 0.1 e.
−0.01 b. 0.01 f.
−0.001 c. 0.001 g.
−0.0001 d. 0.0001 h.

12. [T] [latex]\underset{z\to 0}{\lim}\dfrac{z-1}{z^2(z+3)}[/latex]

[latex]z[/latex] [latex]\frac{z-1}{z^2(z+3)}[/latex] [latex]z[/latex] [latex]\frac{z-1}{z^2(z+3)}[/latex]
−0.1 a. 0.1 e.
−0.01 b. 0.01 f.
−0.001 c. 0.001 g.
−0.0001 d. 0.0001 h.

13. [T] [latex]\underset{t\to 0^+}{\lim}\dfrac{\cos t}{t}[/latex]

[latex]t[/latex] [latex]\frac{\cos t}{t}[/latex]
0.1 a.
0.01 b.
0.001 c.
0.0001 d.

14. [T] [latex]\underset{x\to 2^-}{\lim}\dfrac{1-\frac{2}{x}}{x^2-4}[/latex]

[latex]x[/latex] [latex]\frac{1-\frac{2}{x}}{x^2-4}[/latex] [latex]x[/latex] [latex]\frac{1-\frac{2}{x}}{x^2-4}[/latex]
1.9 a. 2.1 e.
1.99 b. 2.01 f.
1.999 c. 2.001 g.
1.9999 d. 2.0001 h.

In the following exercises (15-16), set up a table of values and round to eight significant digits. Based on the table of values, make a guess about what the limit is. Then, use a calculator to graph the function and determine the limit. Was the conjecture correct? If not, why does the method of tables fail?

15. [T] [latex]\underset{\theta \to 0^-}{\lim}\sin \left(\frac{\pi }{\theta }\right)[/latex]

θ [latex]\sin (\frac{\pi }{\theta })[/latex] θ [latex]\sin (\frac{\pi }{\theta })[/latex]
−0.1 a. 0.1 e.
−0.01 b. 0.01 f.
−0.001 c. 0.001 g.
−0.0001 d. 0.0001 h.

16. [T] [latex]\underset{\alpha \to 0^+}{\lim}\frac{1}{\alpha} \cos \left(\frac{\pi }{\alpha }\right)[/latex]

[latex]a[/latex] [latex]\frac{1}{\alpha } \cos (\frac{\pi }{\alpha })[/latex]
0.1 a.
0.01 b.
0.001 c.
0.0001 d.

In the following exercises (17-20), consider the graph of the function [latex]y=f(x)[/latex] shown here. Which of the statements about [latex]y=f(x)[/latex] are true and which are false? Explain why a statement is false.

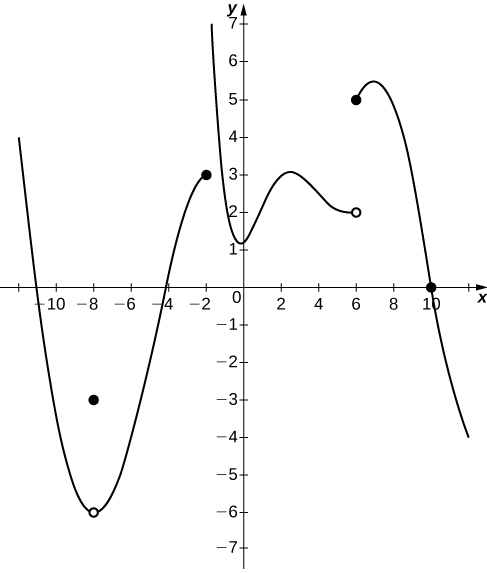
A graph of a piecewise function with three segments and a point. The first segment is a curve opening upward with vertex at (-8, -6). This vertex is an open circle, and there is a closed circle instead at (-8, -3). The segment ends at (-2,3), where there is a closed circle. The second segment stretches up asymptotically to infinity along x=-2, changes direction to increasing at about (0,1.25), increases until about (2.25, 3), and decreases until (6,2), where there is an open circle. The last segment starts at (6,5), increases slightly, and then decreases into quadrant four, crossing the x axis at (10,0). All of the changes in direction are smooth curves.

17. [latex]\underset{x\to 10^-}{\lim}f(x)=0[/latex]

18. [latex]\underset{x\to -2^+}{\lim}f(x)=3[/latex]

19. [latex]\underset{x\to -8^+}{\lim}f(x)=f(-8)[/latex]

20. [latex]\underset{x\to 6}{\lim}f(x)=5[/latex]

In the following exercises (21-24), use the following graph of the function [latex]y=f(x)[/latex] to find the values, if possible. Estimate when necessary.

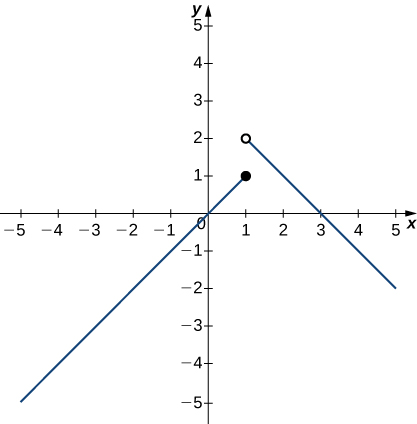
A graph of a piecewise function with two segments. The first segment exists for x <=1, and the second segment exists for x > 1. The first segment is linear with a slope of 1 and goes through the origin. Its endpoint is a closed circle at (1,1). The second segment is also linear with a slope of -1. It begins with the open circle at (1,2).

21. [latex]\underset{x\to 1^-}{\lim}f(x)[/latex]

22. [latex]\underset{x\to 1^+}{\lim}f(x)[/latex]

23. [latex]\underset{x\to 1}{\lim}f(x)[/latex]

24. [latex]\underset{x\to 2}{\lim}f(x)[/latex]
25. [latex]f(1)[/latex]

In the following exercises (26-29), use the graph of the function [latex]y=f(x)[/latex] shown here to find the values, if possible. Estimate when necessary.

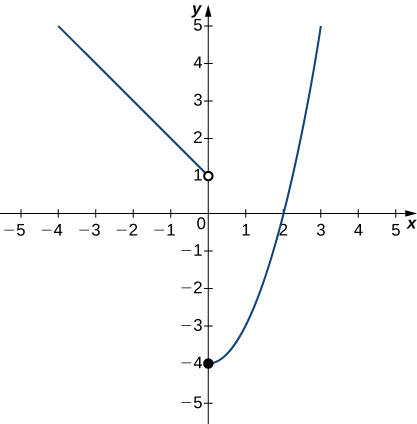
A graph of a piecewise function with two segments. The first is a linear function for x < 0. There is an open circle at (0,1), and its slope is -1. The second segment is the right half of a parabola opening upward. Its vertex is a closed circle at (0, -4), and it goes through the point (2,0).

26. [latex]\underset{x\to 0^-}{\lim}f(x)[/latex]

27. [latex]\underset{x\to 0^+}{\lim}f(x)[/latex]

28. [latex]\underset{x\to 0}{\lim}f(x)[/latex]

29. [latex]\underset{x\to 2}{\lim}f(x)[/latex]

In the following exercises (30-35), use the graph of the function [latex]y=f(x)[/latex] shown here to find the values, if possible. Estimate when necessary.

A graph of a piecewise function with three segments, all linear. The first exists for x < -2, has a slope of 1, and ends at the open circle at (-2, 0). The second exists over the interval [-2, 2], has a slope of -1, goes through the origin, and has closed circles at its endpoints (-2, 2) and (2,-2). The third exists for x>2, has a slope of 1, and begins at the open circle (2,2).

30. [latex]\underset{x\to -2^-}{\lim}f(x)[/latex]

31. [latex]\underset{x\to -2^+}{\lim}f(x)[/latex]

32. [latex]\underset{x\to -2}{\lim}f(x)[/latex]

33. [latex]\underset{x\to 2^-}{\lim}f(x)[/latex]

34. [latex]\underset{x\to 2^+}{\lim}f(x)[/latex]

35. [latex]\underset{x\to 2}{\lim}f(x)[/latex]

In the following exercises (36-38), use the graph of the function [latex]y=g(x)[/latex] shown here to find the values, if possible. Estimate when necessary.

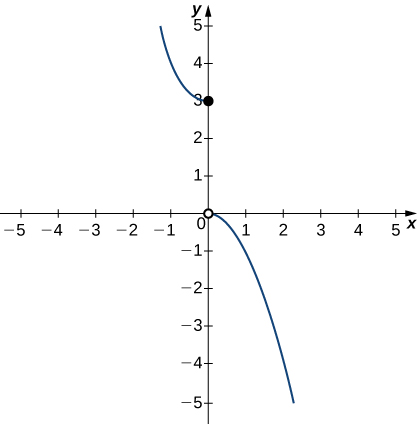
A graph of a piecewise function with two segments. The first exists for x>=0 and is the left half of an upward opening parabola with vertex at the closed circle (0,3). The second exists for x>0 and is the right half of a downward opening parabola with vertex at the open circle (0,0).

36. [latex]\underset{x\to 0^-}{\lim}g(x)[/latex]

37. [latex]\underset{x\to 0^+}{\lim}g(x)[/latex]

38. [latex]\underset{x\to 0}{\lim}g(x)[/latex]

In the following exercises (39-41), use the graph of the function [latex]y=h(x)[/latex] shown here to find the values, if possible. Estimate when necessary.

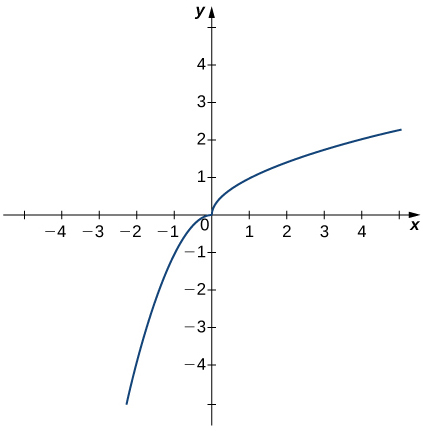
A graph of a function with two curves approaching 0 from quadrant 1 and quadrant 3. The curve in quadrant one appears to be the top half of a parabola opening to the right of the y axis along the x axis with vertex at the origin. The curve in quadrant three appears to be the left half of a parabola opening downward with vertex at the origin.

39. [latex]\underset{x\to 0^-}{\lim}h(x)[/latex]

40. [latex]\underset{x\to 0^+}{\lim}h(x)[/latex]

41. [latex]\underset{x\to 0}{\lim}h(x)[/latex]

In the following exercises (42-46), use the graph of the function [latex]y=f(x)[/latex] shown here to find the values, if possible. Estimate when necessary.

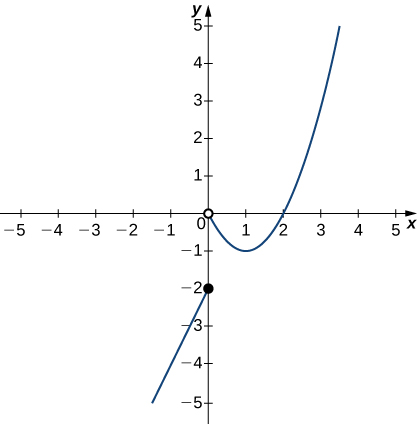
A graph with a curve and a point. The point is a closed circle at (0,-2). The curve is part of an upward opening parabola with vertex at (1,-1). It exists for x > 0, and there is a closed circle at the origin.

42. [latex]\underset{x\to 0^-}{\lim}f(x)[/latex]

43. [latex]\underset{x\to 0^+}{\lim}f(x)[/latex]

44. [latex]\underset{x\to 0}{\lim}f(x)[/latex]

45. [latex]\underset{x\to 1^-}{\lim}f(x)[/latex]

46. [latex]\underset{x\to 2^+}{\lim}f(x)[/latex]

In the following exercises (47-51), sketch the graph of a function with the given properties.

47. [latex]\underset{x\to 2}{\lim}f(x)=1, \, \underset{x\to 4^-}{\lim}f(x)=3[/latex], [latex]\underset{x\to 4^+}{\lim}f(x)=6, \, f(4)[/latex] is not defined.

48. [latex]\underset{x\to -\infty }{\lim}f(x)=0, \, \underset{x\to -1^-}{\lim}f(x)=−\infty[/latex], [latex]\underset{x\to -1^+}{\lim}f(x)=\infty, \, \underset{x\to 0}{\lim}f(x)=f(0), \, f(0)=1, \, \underset{x\to \infty }{\lim}f(x)=−\infty[/latex]

49. [latex]\underset{x\to -\infty}{\lim}f(x)=2, \, \underset{x\to 3^-}{\lim}f(x)=−\infty[/latex], [latex]\underset{x\to 3^+}{\lim}f(x)=\infty, \, \underset{x\to \infty }{\lim}f(x)=2, \, f(0)=-\frac{1}{3}[/latex]

50. [latex]\underset{x\to -\infty }{\lim}f(x)=2, \, \underset{x\to -2}{\lim}f(x)=−\infty[/latex],[latex]\underset{x\to \infty }{\lim}f(x)=2, \, f(0)=0[/latex]

51. [latex]\underset{x\to -\infty }{\lim}f(x)=0, \, \underset{x\to -1^-}{\lim}f(x)=\infty, \, \underset{x\to -1^+}{\lim}f(x)=−\infty, \, f(0)=-1, \, \underset{x\to 1^-}{\lim}f(x)=−\infty, \, \underset{x\to 1^+}{\lim}f(x)=\infty, \, \underset{x\to \infty }{\lim}f(x)=0[/latex]

52. Shock waves arise in many physical applications, ranging from supernovas to detonation waves. A graph of the density of a shock wave with respect to distance, [latex]x[/latex], is shown here. We are mainly interested in the location of the front of the shock, labeled [latex]x_{SF}[/latex] in the diagram.

A graph in quadrant one of the density of a shockwave with three labeled points: p1 and p2 on the y axis, with p1 > p2, and xsf on the x axis. It consists of y= p1 from 0 to xsf, x = xsf from y= p1 to y=p2, and y=p2 for values greater than or equal to xsf.

a. Evaluate [latex]\underset{x\to x_{SF}^+}{\lim}\rho(x)[/latex]

b. Evaluate [latex]\underset{x\to x_{SF}^-}{\lim}\rho(x)[/latex]

c. Evaluate [latex]\underset{x\to x_{SF}}{\lim}\rho(x)[/latex]. Explain the physical meanings behind your answers.

53. A track coach uses a camera with a fast shutter to estimate the position of a runner with respect to time. A table of the values of position of the athlete versus time is given here, where [latex]x[/latex] is the position in meters of the runner and [latex]t[/latex] is time in seconds. What is [latex]\underset{t\to 2}{\lim}x(t)[/latex]? What does it mean physically?

[latex]t[/latex] (sec) [latex]x[/latex] (m)
1.75 4.5
1.95 6.1
1.99 6.42
2.01 6.58
2.05 6.9
2.25 8.5