Putting It Together: Applications of Derivatives

A Rocket Launch

A rocket is launched so that it rises vertically. A camera is positioned [latex]5000[/latex] ft from the launch pad. When the rocket is [latex]1000[/latex] ft above the launch pad, its velocity is [latex]600[/latex] ft/sec. Find the necessary rate of change of the camera’s angle as a function of time so that it stays focused on the rocket.

Step 1. Draw a picture introducing the variables.

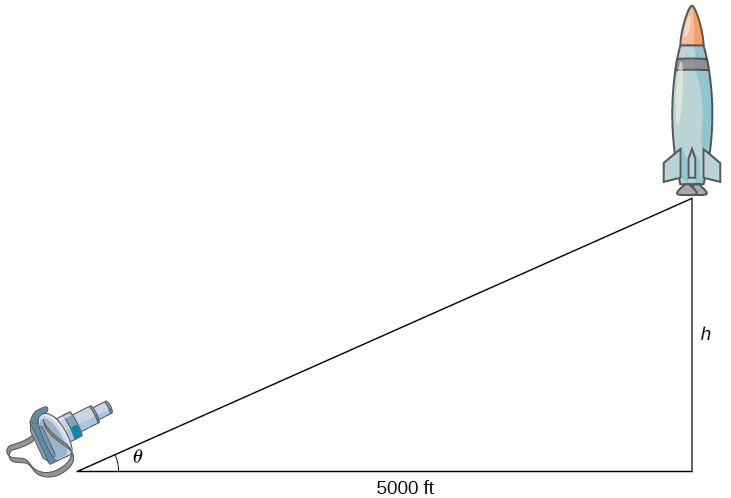
A right triangle is formed with a camera at one of the nonright angles and a rocket at the other nonright angle. The angle with the camera has measure θ. The distance from the rocket to the ground is h; note that this is the side opposite the angle with measure θ. The side adjacent to the angle with measure θ is 5000 ft.

Figure 2. A camera is positioned 5000 ft from the launch pad of the rocket. The height of the rocket and the angle of the camera are changing with respect to time. We denote those quantities with the variables [latex]h[/latex] and [latex]\theta[/latex], respectively.

Let [latex]h[/latex] denote the height of the rocket above the launch pad and [latex]\theta[/latex] be the angle between the camera lens and the ground.

Step 2. We are trying to find the rate of change in the angle of the camera with respect to time when the rocket is [latex]1000[/latex] ft off the ground. That is, we need to find [latex]\frac{d\theta}{dt}[/latex] when [latex]h=1000[/latex] ft. At that time, we know the velocity of the rocket is [latex]\frac{dh}{dt}=600[/latex] ft/sec.

Step 3. Now we need to find an equation relating the two quantities that are changing with respect to time: [latex]h[/latex] and [latex]\theta[/latex]. How can we create such an equation? Using the fact that we have drawn a right triangle, it is natural to think about trigonometric functions. Recall that [latex]\tan \theta[/latex] is the ratio of the length of the opposite side of the triangle to the length of the adjacent side. Thus, we have

[latex]\tan \theta =\frac{h}{5000}[/latex].

This gives us the equation

[latex]h=5000 \tan \theta[/latex].

Step 4. Differentiating this equation with respect to time [latex]t[/latex], we obtain

[latex]\frac{dh}{dt}=5000 \sec^2 \theta \frac{d\theta}{dt}[/latex].

Step 5. We want to find [latex]\frac{d\theta}{dt}[/latex] when [latex]h=1000[/latex] ft. At this time, we know that [latex]\frac{dh}{dt}=600[/latex] ft/sec. We need to determine [latex]\sec^2 \theta[/latex]. Recall that [latex]\sec \theta[/latex] is the ratio of the length of the hypotenuse to the length of the adjacent side. We know the length of the adjacent side is [latex]5000[/latex] ft. To determine the length of the hypotenuse, we use the Pythagorean theorem, where the length of one leg is [latex]5000[/latex] ft, the length of the other leg is [latex]h=1000[/latex] ft, and the length of the hypotenuse is [latex]c[/latex] feet as shown in the following figure.

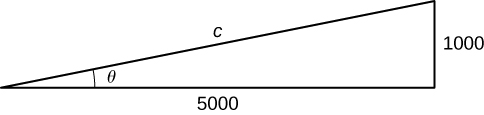
A right triangle has one angle with measure θ. The hypotenuse is c, the side length opposite the angle with measure θ is 1000, and the side adjacent to the angle with measure θ is 5000.

We see that

[latex]1000^2+5000^2=c^2[/latex]

and we conclude that the hypotenuse is

[latex]c=1000\sqrt{26}[/latex] ft.

Therefore, when [latex]h=1000[/latex], we have

[latex]\sec^2 \theta =(\frac{1000\sqrt{26}}{5000})^2=\frac{26}{25}[/latex].

Recall from step 4 that the equation relating [latex]\frac{d\theta}{dt}[/latex] to our known values is

[latex]\frac{dh}{dt}=5000 \sec^2 \theta \frac{d\theta}{dt}[/latex].

When [latex]h=1000[/latex] ft, we know that [latex]\frac{dh}{dt}=600[/latex] ft/sec and [latex]\sec^2 \theta =\frac{26}{25}[/latex]. Substituting these values into the previous equation, we arrive at the equation

[latex]600=5000(\frac{26}{25})\frac{d\theta}{dt}[/latex].

Therefore, [latex]\frac{d\theta}{dt}=\frac{3}{26}[/latex] rad/sec.