Related-Rates Problem-Solving

Learning Outcomes

Express changing quantities in terms of derivatives.
Find relationships among the derivatives in a given problem.
Use the chain rule to find the rate of change of one quantity that depends on the rate of change of other quantities.

Setting up Related-Rates Problems

In many real-world applications, related quantities are changing with respect to time. For example, if we consider the balloon example again, we can say that the rate of change in the volume, [latex]V[/latex], is related to the rate of change in the radius, [latex]r[/latex]. In this case, we say that [latex]\frac{dV}{dt}[/latex] and [latex]\frac{dr}{dt}[/latex] are related rates because [latex]V[/latex] is related to [latex]r[/latex]. Here we study several examples of related quantities that are changing with respect to time and we look at how to calculate one rate of change given another rate of change.

Example: Inflating a Balloon

A spherical balloon is being filled with air at the constant rate of [latex]2 \, \frac{\text{cm}^3}{\text{sec}}[/latex] (Figure 1). How fast is the radius increasing when the radius is [latex]3\, \text{cm}[/latex]?

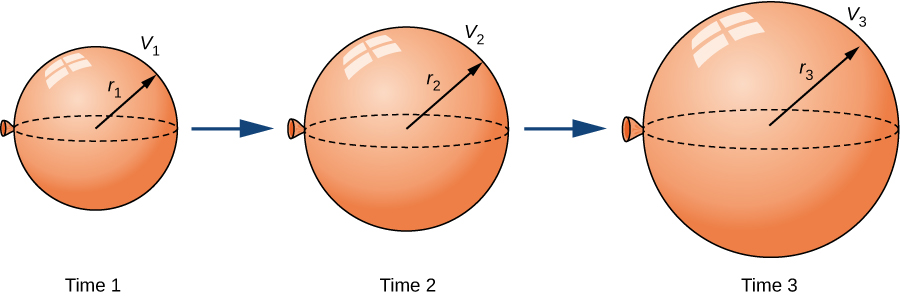
Three balloons are shown at Times 1, 2, and 3. These balloons increase in volume and radius as time increases.

Figure 1. As the balloon is being filled with air, both the radius and the volume are increasing with respect to time.

Show Solution

Watch the following video to see the worked solution to Example: Inflating a Balloon.

Closed Captioning and Transcript Information for Video

Try It

What is the instantaneous rate of change of the radius when [latex]r=6 \, \text{cm}[/latex]?

Hint

Show Solution

Try It

Before looking at other examples, let’s outline the problem-solving strategy we will be using to solve related-rates problems.

Problem-Solving Strategy: Solving a Related-Rates Problem

Assign symbols to all variables involved in the problem. Draw a figure if applicable.
State, in terms of the variables, the information that is given and the rate to be determined.
Find an equation relating the variables introduced in step 1.
Using the chain rule, differentiate both sides of the equation found in step 3 with respect to the independent variable. This new equation will relate the derivatives.
Substitute all known values into the equation from step 4, then solve for the unknown rate of change.

We are able to solve related-rates problems using a similar approach to implicit differentiation. In the example below, we are required to take derivatives of different variables with respect to time [latex]{t}[/latex], ie. [latex]{s}[/latex] and [latex]{x}[/latex]. When this happens, we can attach a [latex]\frac{ds}{dt}[/latex] or a [latex]\frac{dx}{dt}[/latex] to the derivative, just as we did in implicit differentiation.

Note that when solving a related-rates problem, it is crucial not to substitute known values too soon. For example, if the value for a changing quantity is substituted into an equation before both sides of the equation are differentiated, then that quantity will behave as a constant and its derivative will not appear in the new equation found in step 4. We examine this potential error in the following example.

Examples of the Process

Let’s now implement the strategy just described to solve several related-rates problems. The first example involves a plane flying overhead. The relationship we are studying is between the speed of the plane and the rate at which the distance between the plane and a person on the ground is changing.

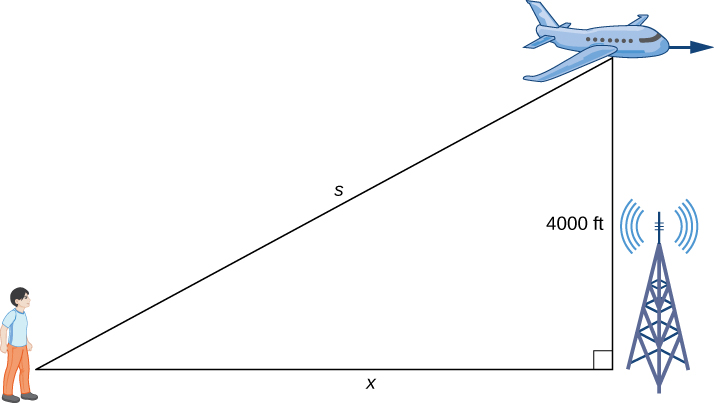
Example: An Airplane Flying at a Constant Elevation

An airplane is flying overhead at a constant elevation of [latex]4000[/latex] ft. A man is viewing the plane from a position [latex]3000[/latex] ft from the base of a radio tower. The airplane is flying horizontally away from the man. If the plane is flying at the rate of [latex]600[/latex] ft/sec, at what rate is the distance between the man and the plane increasing when the plane passes over the radio tower?

Show Solution

Step 1. Draw a picture, introducing variables to represent the different quantities involved.

A right triangle is made with a person on the ground, an airplane in the air, and a radio tower at the right angle on the ground. The hypotenuse is s, the distance on the ground between the person and the radio tower is x, and the side opposite the person (that is, the height from the ground to the airplane) is 4000 ft.

Figure 2. An airplane is flying at a constant height of 4000 ft. The distance between the person and the airplane and the person and the place on the ground directly below the airplane are changing. We denote those quantities with the variables [latex]s[/latex] and [latex]x[/latex], respectively.

As shown, [latex]x[/latex] denotes the distance between the man and the position on the ground directly below the airplane. The variable [latex]s[/latex] denotes the distance between the man and the plane. Note that both [latex]x[/latex] and [latex]s[/latex] are functions of time. We do not introduce a variable for the height of the plane because it remains at a constant elevation of [latex]4000[/latex] ft. Since an object’s height above the ground is measured as the shortest distance between the object and the ground, the line segment of length [latex]4000[/latex] ft is perpendicular to the line segment of length [latex]x[/latex] feet, creating a right triangle.

Step 2. Since [latex]x[/latex] denotes the horizontal distance between the man and the point on the ground below the plane, [latex]dx/dt[/latex] represents the speed of the plane. We are told the speed of the plane is 600 ft/sec. Therefore, [latex]\frac{dx}{dt}=600[/latex] ft/sec. Since we are asked to find the rate of change in the distance between the man and the plane when the plane is directly above the radio tower, we need to find [latex]ds/dt[/latex] when [latex]x=3000[/latex] ft.

Step 3. From Figure 2, we can use the Pythagorean theorem to write an equation relating [latex]x[/latex] and [latex]s[/latex]:

[latex][x(t)]^2+4000^2=[s(t)]^2[/latex].

Step 4. Differentiating this equation with respect to time and using the fact that the derivative of a constant is zero, we arrive at the equation

[latex]x\frac{dx}{dt}=s\frac{ds}{dt}[/latex].

Step 5. Find the rate at which the distance between the man and the plane is increasing when the plane is directly over the radio tower. That is, find [latex]\frac{ds}{dt}[/latex] when [latex]x=3000[/latex] ft. Since the speed of the plane is [latex]600[/latex] ft/sec, we know that [latex]\frac{dx}{dt}=600[/latex] ft/sec. We are not given an explicit value for [latex]s[/latex]; however, since we are trying to find [latex]\frac{ds}{dt}[/latex] when [latex]x=3000[/latex] ft, we can use the Pythagorean theorem to determine the distance [latex]s[/latex] when [latex]x=3000[/latex] and the height is [latex]4000[/latex] ft. Solving the equation

[latex]3000^2+4000^2=s^2[/latex]

for [latex]s[/latex], we have [latex]s=5000[/latex] ft at the time of interest. Using these values, we conclude that [latex]ds/dt[/latex] is a solution of the equation

[latex](3000)(600)=(5000) \cdot \frac{ds}{dt}[/latex].

Therefore,

[latex]\frac{ds}{dt}=\frac{3000 \cdot 600}{5000}=360[/latex] ft/sec.

Note: When solving related-rates problems, it is important not to substitute values for the variables too soon. For example, in step 3, we related the variable quantities [latex]x(t)[/latex] and [latex]s(t)[/latex] by the equation

[latex][x(t)]^2+4000^2=[s(t)]^2[/latex].

Since the plane remains at a constant height, it is not necessary to introduce a variable for the height, and we are allowed to use the constant 4000 to denote that quantity. However, the other two quantities are changing. If we mistakenly substituted [latex]x(t)=3000[/latex] into the equation before differentiating, our equation would have been

[latex]3000^2+4000^2=[s(t)]^2[/latex].

After differentiating, our equation would become

[latex]0=s(t)\frac{ds}{dt}[/latex].

As a result, we would incorrectly conclude that [latex]\frac{ds}{dt}=0[/latex].

Watch the following video to see the worked solution to Example: An Airplane Flying at a Constant Elevation.

Closed Captioning and Transcript Information for Video

Try It

What is the speed of the plane if the distance between the person and the plane is increasing at the rate of [latex]300[/latex] ft/sec?

Hint

Show Solution

Try It

What rate of change is necessary for the elevation angle of the camera if the camera is placed on the ground at a distance of [latex]4000[/latex] ft from the launch pad and the velocity of the rocket is [latex]500[/latex] ft/sec when the rocket is [latex]2000[/latex] ft off the ground?

Hint

Show Solution

Try It

In the next example, we consider water draining from a cone-shaped funnel. We compare the rate at which the level of water in the cone is decreasing with the rate at which the volume of water is decreasing.

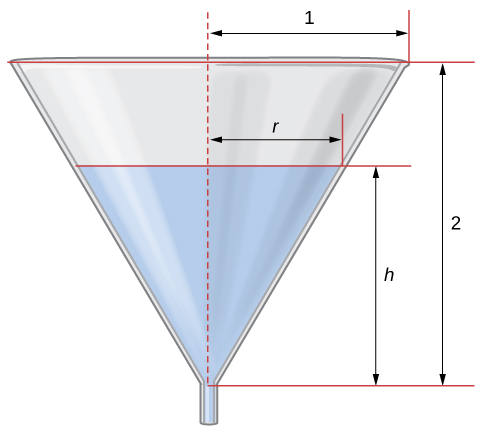
Example: Water Draining from a Funnel

Water is draining from the bottom of a cone-shaped funnel at the rate of [latex]0.03 \, \text{ft}^3 /\text{sec}[/latex]. The height of the funnel is [latex]2[/latex] ft and the radius at the top of the funnel is [latex]1[/latex] ft. At what rate is the height of the water in the funnel changing when the height of the water is [latex]\frac{1}{2}[/latex] ft?

Show Solution

Try It

At what rate is the height of the water changing when the height of the water is [latex]\frac{1}{4}[/latex] ft?

Show Solution

Module 4: Applications of Derivatives