Skills Review for Applied Optimization Problems

Learning Outcomes

  • Calculate the volume of rectangular solid
  • Use the Pythagorean theorem to find the unknown side length of a right triangle
  • Use the distance, rate, and time formula
  • Write an equation in one variable to solve problems with multiple unknowns

In the Applied Optimization Problems section, we will use formulas to model real-life scenarios. Calculus will then be used to either maximize or minimize the given scenario. For example, we can find the maximum area we can enclose with a given amount of fence. To review some of the formulas needed for the Applied Optimization Problems section, see Skills Review for Related Rates. Specifically, pay close attention to the outcomes listed above.

One Variable for Multiple Unknowns

We sometimes define unknown measurements or values based on another unknown. This allows us to solve for a single variable rather than having multiple variables complicating the algebra.

When dealing with real-world applications, there are certain expressions that we can translate directly into math. The table below lists some common verbal expressions and their equivalent mathematical expressions.

Verbal Translation to Math Operations
One number exceeds another by a [latex]x,\text{ }x+a[/latex]
Twice a number [latex]2x[/latex]
One number is a more than another number [latex]x,\text{ }x+a[/latex]
One number is a less than twice another number [latex]x,2x-a[/latex]
The product of a number and a, decreased by b [latex]ax-b[/latex]
The quotient of a number and the number plus a is three times the number [latex]\Large\frac{x}{x+a}\normalsize =3x[/latex]
The product of three times a number and the number decreased by b is c [latex]3x\left(x-b\right)=c[/latex]

 

How To: Given a real-world situation, write a linear equation to model it

  1. Identify known and unknown quantities.
  2. Assign a variable to represent the unknown quantity.
  3. If there is more than one unknown quantity, find a way to write the second unknown in terms of the first.
  4. Write an equation interpreting the words in the problem as mathematical operations.
  5. Solve the equation, check to be sure your answer is reasonable, and give the answer using the language and units of the original situation.

Example

Find a linear equation to solve for the following unknown quantities: One number exceeds another number by [latex]17[/latex] and their sum is [latex]31[/latex]. Find the two numbers.

Try It

Find a linear equation to solve for the following unknown quantities: One number is three more than twice another number. If the sum of the two numbers is [latex]36[/latex], find the numbers.

We can also use a linear equation in one variable to solve a problem with two unknowns by writing an expression for one unknown in terms of the other.

example: write a linear equation in one variable to model and solve an application

A bag is filled with green and blue marbles. There are 77 marbles in the bag. If there are 17 more green marbles than blue marbles, find the number of green marbles and the number of blue marbles in the bag.

How many marbles of each color are in the bag?

Watch the following video for another example of using a linear equation in one variable to solve an application.

Try it

A cash register contains only five dollar and ten dollar bills. It contains twice as many five’s as ten’s and the total amount of money in the cash register is 560 dollars. How many ten’s are in the cash register?

Many applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Sometimes, these problems involve two equations representing two unknowns, which can be written using one equation in one variable by expressing one unknown in terms of the other. Examples of formulas include the perimeter of a rectangle, [latex]P=2L+2W[/latex]; the area of a rectangular region, [latex]A=LW[/latex]; and the volume of a rectangular solid, [latex]V=LWH[/latex].

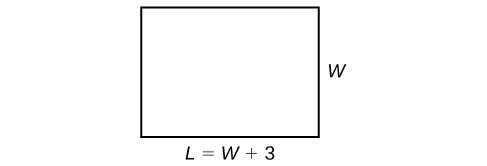
Example: Solving a Perimeter Problem

The perimeter of a rectangular outdoor patio is [latex]54[/latex] ft. The length is [latex]3[/latex] ft. greater than the width. What are the dimensions of the patio?

Evaluating a variable for an expression

In the example above, the length was written in terms of the width in order to substitute it for the variable [latex]L[/latex] to be able to write one equation in one variable.

This is a powerful technique in algebra and should be practiced until it becomes familiar, so it’s worth taking a closer look.

Try It

Find the dimensions of a rectangle given that the perimeter is [latex]110[/latex] cm. and the length is 1 cm. more than twice the width.

Example: Solving an Area Problem

The perimeter of a tablet of graph paper is 48 in2. The length is [latex]6[/latex] in. more than the width. Find the area of the graph paper.

Try It

A game room has a perimeter of 70 ft. The length is five more than twice the width. How many ft2 of new carpeting should be ordered?