Skills Review for Derivatives and the Shape of a Graph

Learning Outcomes

  • Identify extrema and increasing and decreasing intervals
  • Use a sign chart to determine where a function is positive or negative

In the Derivatives and the Shape of a Graph section, we will analyze graphs of functions using calculus. Here we will review identifying extrema and increasing and decreasing intervals of a function along with how to create sign charts to determine where a certain equation is positive or negative.

Identify Extrema and Increasing and Decreasing Intervals

We say that a function is increasing on an interval if the function values increase as the input values increase within that interval. Similarly, a function is decreasing on an interval if the function values decrease as the input values increase over that interval. The graph below shows examples of increasing and decreasing intervals on a function.

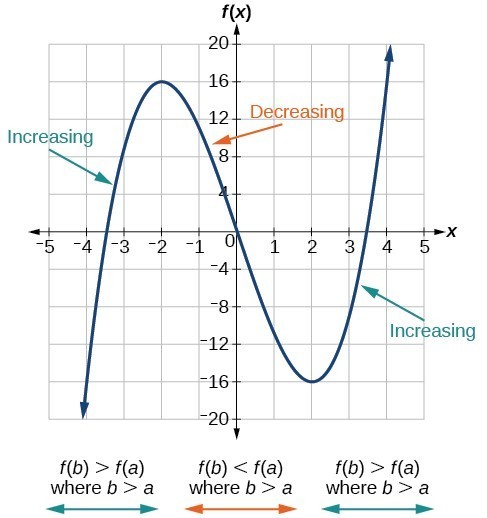
Graph of a polynomial that shows the increasing and decreasing intervals and local maximum and minimum.

The function [latex]f\left(x\right)={x}^{3}-12x[/latex] is increasing on [latex]\left(-\infty \text{,}-\text{2}\right){{\cup }^{\text{ }}}^{\text{ }}\left(2,\infty \right)[/latex] and is decreasing on [latex]\left(-2\text{,}2\right)[/latex].

This video further explains how to find where a function is increasing or decreasing.

A value of the output where a function changes from increasing to decreasing (as we go from left to right, that is, as the input variable increases) is called a local maximum. If a function has more than one, we say it has local maxima. Similarly, a value of the output where a function changes from decreasing to increasing as the input variable increases is called a local minimum. The plural form is “local minima.” Together, local maxima and minima are called local extrema, or local extreme values, of the function. Often, the term local is replaced by the term relative.

For the function below, the local maximum is 16, and it occurs at [latex]x=-2[/latex]. The local minimum is [latex]-16[/latex] and it occurs at [latex]x=2[/latex].

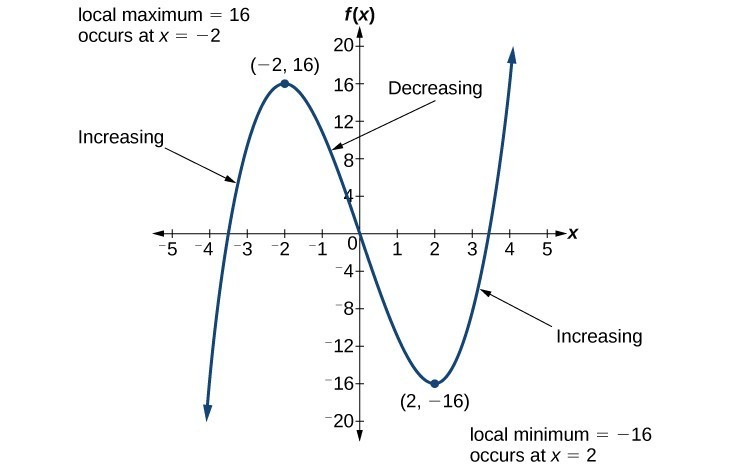
Graph of a polynomial that shows the increasing and decreasing intervals and local maximum and minimum. The local maximum is 16 and occurs at x = negative 2. This is the point negative 2, 16. The local minimum is negative 16 and occurs at x = 2. This is the point 2, negative 16.

To locate the local maxima and minima from a graph, we need to observe the graph to determine where the graph attains its highest and lowest points, respectively, within an open interval. Like the summit of a roller coaster, the graph of a function is higher at a local maximum than at nearby points on both sides. The graph will also be lower at a local minimum than at neighboring points. The graph below illustrates these ideas for a local maximum.

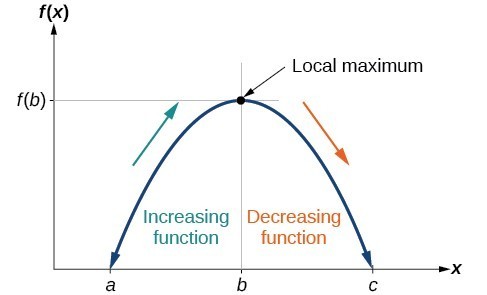
Graph of a polynomial that shows the increasing and decreasing intervals and local maximum.

Definition of a local maximum.

These observations lead us to a formal definition of local extrema.

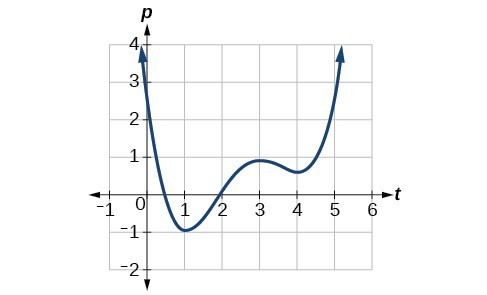
Example: Finding Increasing and Decreasing Intervals on a Graph

Given the function [latex]p\left(t\right)[/latex] in the graph below, identify the intervals on which the function appears to be increasing.

Graph of a polynomial. As x gets large in the negative direction, the outputs of the function get large in the positive direction. As inputs approach 1, then the function value approaches a minimum of negative one. As x approaches 3, the values increase again and between 3 and 4 decrease one last time. As x gets large in the positive direction, the function values increase without bound.

Try It

Example: Finding Local Maxima and Minima from a Graph

For the function [latex]f[/latex] whose graph is shown below, find all local maxima and minima.

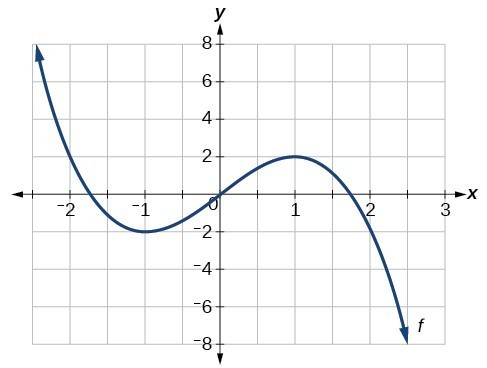
Graph of a polynomial. The line curves down to x = negative 2 and up to x = 1.

Try It

Use a Sign Chart to Determine Where a Function is Positive or Negative

A sign chart can be created to determine where a function equation is positive or negative. Equations most often change signs only where the equation is equal to zero. Graphically, where an equation is equal to zero is an [latex]x[/latex]-intercept. It is at these [latex]x[/latex]-intercepts that an equation can go from being above the [latex]x[/latex]-axis (positive) to being below the [latex]x[/latex]-axis (negative) or vice-versa.

To create a sign chart (number line), we will use the critical points (where a given equation is equal to zero or not defined) to divide the number line into intervals and then determine whether the function equation is positive or negative in the interval. We then determine where the function equation is positive or negative.

Example: Determining Where a Function is Positive or Negative

Solve [latex]x^2-x-12 \ge{0}[/latex] algebraically. Write the solution in interval notation.

Try It

Solve [latex]x^2+2x-8 \ge{0}[/latex] algebraically. Write the solution in interval notation.

Try It

Solve [latex]x^2-2x-15 \le{0}[/latex] algebraically. Write the solution in interval notation.

In the previous example, since the expression [latex]x^2-x-12[/latex] factors nicely, we can find the sign of each of the factors, and then the sign of the product. Our number line would look like this:

The figure shows the expression x squared minus x minus 12 factored to the quantity of x plus 3 times the quantity of x minus 4. The image shows a number line showing dotted lines on negative 3 and 4. It shows the signs of the quantity x plus 3 to be negative, positive, positive, and the signs of the quantity x minus 4 to be negative, negative, positive. Under the number line, it shows the quantity x plus 3 times the quantity x minus 4 with the signs positive, negative, positive.

The result is the same as we found using the other method.