In the Related Rates section, we will take derivatives of various mathematical formulas. Here we will review the formulas for calculating volume of a cone, volume of a sphere, and volume of a rectangular solid. We will also briefly review the Pythagorean Theorem and the distance, rate, and time formula.

Find the Volume of a Cone

The volume of a cone can be found using the following formula:

[latex]V=\frac{1}{3}\pi r^2h[/latex]

where [latex]r[/latex] is the radius of the circular base of the cone and [latex]h[/latex] is the height of the cone.

Find the Volume of a Sphere

The volume of a sphere can be found using the following formula:

[latex]V=\frac{4}{3}\pi r^3[/latex]

where [latex]r[/latex] is the radius.

Find the Volume of a Rectangular Solid

A rectangular solid has a length, width, and height. The volume of a rectangular solid can be found using the following formula:

[latex]V=lwh[/latex]

where [latex]l[/latex] is the length, [latex]w[/latex] is the width, and [latex]h[/latex] is the height.

Use the Pythagorean Theorem

The Pythagorean theorem is a statement about the sides of a right triangle. One of the angles of a right triangle is always equal to [latex]90[/latex] degrees. This angle is the right angle. The two sides next to the right angle are called the legs and the other side is called the hypotenuse. The hypotenuse is the side opposite the right angle, and it is always the longest side.

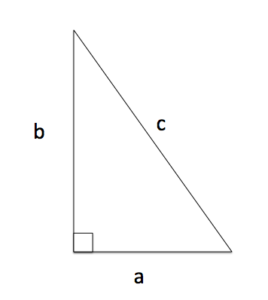
A right triangle with sides labeled.

The Pythagorean theorem is often used to find unknown lengths of the sides of right triangles. If the longest leg of a right triangle is labeled c, and the other two a, and b as in the image on the left,  The Pythagorean Theorem states that

[latex]a^2+b^2=c^2[/latex]

Given enough information, we can solve for an unknown length.

In each of the following examples, we will use the Pythagorean theorem to find a missing side of a right triangle.

Use the Distance, Rate, and Time Formula

For an object moving at a uniform (constant) rate, the distance, [latex]d[/latex], traveled is:

[latex]d=rt[/latex]

where [latex]r[/latex] is the rate and [latex]t[/latex] is the time.