Skills Review for Continuity

Learning Outcomes

  • Find the domain of a function algebraically
  • Determine the input values for which a function is discontinuous
  • Graph a piecewise function using domain

The Continuity section will explore the relationship between limits and continuity. To prepare you for this, we will review some of the various types of discontinuities you have previously encountered on your mathematical journey.

Classify Discontinuities of Rational Functions

In general, to find the domain of a rational function, we need to determine which inputs would cause division by zero.

A General Note: Domain of a Rational Function

The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.

How To: Given a rational function, find the domain.

  1. Set the denominator equal to zero.
  2. Solve to find the values of the variable that cause the denominator to equal zero.
  3. The domain contains all real numbers except those found in Step 2.

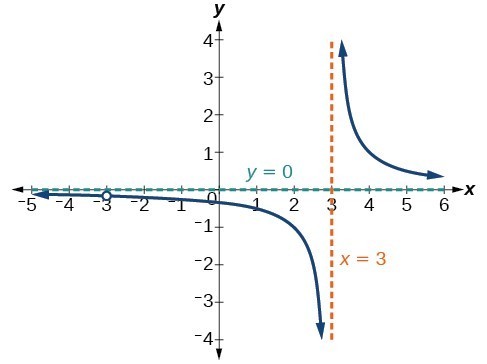
Example: Finding the Domain of a Rational Function

Find the domain of [latex]f\left(x\right)=\dfrac{x+3}{{x}^{2}-9}[/latex].

Try It

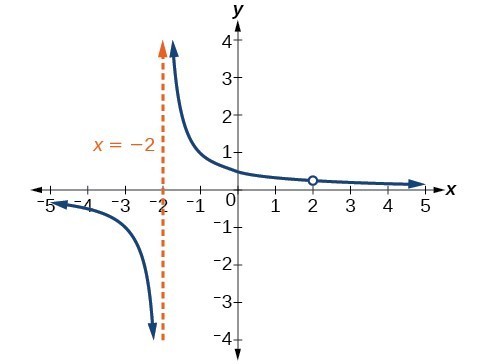
Find the domain of [latex]f\left(x\right)=\dfrac{4x}{5\left(x - 1\right)\left(x - 5\right)}[/latex].

Try It

Values that are restricted from the domain of a rational function are values where the rational function has either a vertical asymptote or a hole (removable discontinuity).

A vertical asymptote of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors. In other words, once you factor and simplify the rational function, vertical asymptotes occur at values that cause the denominator of the simplified rational function to equal 0.

How To: Given a rational function, identify any vertical asymptotes of its graph.

  1. Factor the numerator and denominator.
  2. Simplify the expression by canceling common factors in the numerator and the denominator.
  3. Note any values that cause the denominator to be zero in this simplified version. These are the values where the vertical asymptotes occur.

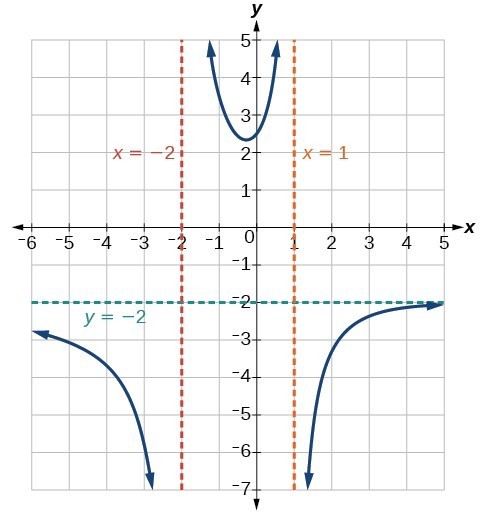
Example: Identifying Vertical Asymptotes

Find the vertical asymptotes of the graph of [latex]k\left(x\right)=\dfrac{5+2{x}^{2}}{2-x-{x}^{2}}[/latex].

Occasionally, a graph will contain a hole: a single point where the graph is not defined, indicated by an open circle. We call such a hole a removable discontinuity.

For example, the function [latex]f\left(x\right)=\dfrac{{x}^{2}-1}{{x}^{2}-2x - 3}[/latex] may be re-written by factoring the numerator and the denominator.

[latex]f\left(x\right)=\dfrac{\left(x+1\right)\left(x - 1\right)}{\left(x+1\right)\left(x - 3\right)}[/latex]

Notice that [latex]x+1[/latex] is a common factor to the numerator and the denominator. The zero of this factor, [latex]x=-1[/latex], is the location of the removable discontinuity. Notice also that [latex]x - 3[/latex] is not a factor in both the numerator and denominator. The zero of this factor, [latex]x=3[/latex], is the vertical asymptote.

Graph of f(x)=(x^2-1)/(x^2-2x-3) with its vertical asymptote at x=3 and a removable discontinuity at x=-1.

A General Note: Removable Discontinuities of Rational Functions

A removable discontinuity occurs in the graph of a rational function at [latex]x=a[/latex] if a is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.

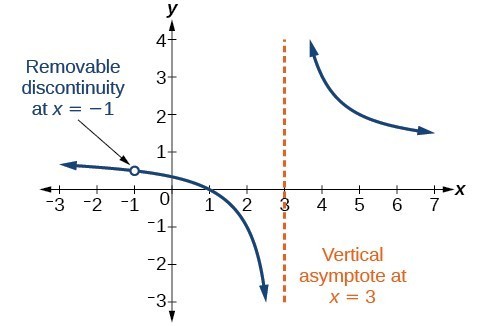
Example: Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Find the vertical asymptotes and removable discontinuities of the graph of [latex]k\left(x\right)=\dfrac{x - 2}{{x}^{2}-4}[/latex].

Try It

Determine Whether a Piecewise Function is Continuous at Its Boundary Value

Recall that a piecewise function, also called a piecewise-defined function, is a function in which more than one formula is used to define the output over different pieces of the domain.

A General Note: Piecewise Functions

A piecewise function is a function in which more than one formula is used to define the output. Each formula has its own domain, and the domain of the function is the union of all these smaller domains. We notate this idea like this:

[latex]f\left(x\right)=\begin{cases}\text{formula 1 if x is in domain 1}\\ \text{formula 2 if x is in domain 2}\\ \text{formula 3 if x is in domain 3}\end{cases}[/latex]

A number in the domain where a piecewise function switches from one piece to the next is called a boundary value. Sometimes, a piecewise function is not continuous at its boundary value(s) and thus can have a discontinuity at a boundary value. In the example below, 2 is a boundary value.

[latex]f\left(x\right)=\begin{cases}\text{formula 1 if } x<2\\ \text{formula 2 if } x\geq2\\ \end{cases}[/latex]

How To: Given a piecewise function, Determine if it is discontinuous at its boundary value(S)

  1. Identify the boundary value(s) of the piecewise function. For every formula (piece) the boundary value is listed by, plug the boundary value into that piece.
  2. To be continuous at a boundary value, all pieces evaluated in step 1 must produce the same function value. If the same function value is not produced, the piecewise-defined function is discontinuous at its boundary value.

Example: Determining Whether a Piecewise function is continuous at its boundary value(S)

Determine whether the function is continuous at its boundary value.

[latex]f\left(x\right)=\begin{cases}\begin{align}{ x }^{2}-4 \hspace{2mm}&\text{ if }\hspace{2mm}{ x }\le{ -3 }\\ { x+8 } \hspace{2mm}&\text{ if }\hspace{2mm}{ x }>{ -3 }\end{align}\end{cases}[/latex]

Example: Determining Whether a Piecewise function is continuous at its boundary value(S)

Determine whether the function is continuous at each of its boundary values.

[latex]f\left(x\right)=\begin{cases}\begin{align}{ x }^{2} \hspace{2mm}&\text{ if }\hspace{2mm}{ x }\le{ 1 }\\ { 3 } \hspace{2mm}&\text{ if }\hspace{2mm} { 1 }<{ x }\le 2\\ { x } \hspace{2mm}&\text{ if }\hspace{2mm}{ x }>{ 2 }\end{align}\end{cases}[/latex]

Try IT