In The Chain Rule section, you will learn how to take the derivative of composed functions. Here we will review some basics about function composition and how it basically involves plugging one function into another. Knowledge about function composition, including how to plug one function into another, will also be useful in the Derivatives of Inverse Function section as you learn about the Inverse Function Theorem. Lastly, to help with simplifying derivatives of functions that require the use of the chain rule, we will review factoring common binomial factors from algebraic expressions.

Find Composite Functions

We can create functions by composing them. The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. The resulting function is known as a composite function. We represent this combination by the following notation:

[latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex]

We read the left-hand side as [latex]``f[/latex] composed with [latex]g[/latex] at [latex]x,''[/latex] and the right-hand side as [latex]``f[/latex] of [latex]g[/latex] of [latex]x.''[/latex] The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol [latex]\circ [/latex] is called the composition operator. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value.

It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside. In the equation above, the function [latex]g[/latex] takes the input [latex]x[/latex] first and yields an output [latex]g\left(x\right)[/latex]. Then the function [latex]f[/latex] takes [latex]g\left(x\right)[/latex] as an input and yields an output [latex]f\left(g\left(x\right)\right)[/latex].

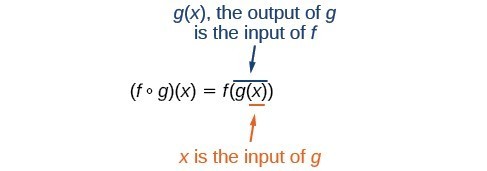
In general [latex]f\circ g[/latex] and [latex]g\circ f[/latex] are different functions. In other words in many cases [latex]f\left(g\left(x\right)\right)\ne g\left(f\left(x\right)\right)[/latex] for all [latex]x[/latex].

For example if [latex]f\left(x\right)={x}^{2}[/latex] and [latex]g\left(x\right)=x+2[/latex], then

[latex]\begin{align}f\left(g\left(x\right)\right)&=f\left(x+2\right) \\[2mm] &={\left(x+2\right)}^{2} \\[2mm] &={x}^{2}+4x+4\hfill \end{align}[/latex]

but

[latex]\begin{align}g\left(f\left(x\right)\right)&=g\left({x}^{2}\right) \\[2mm] \text{ }&={x}^{2}+2\hfill \end{align}[/latex]

These expressions are not equal.

Factor Common Binomial Factors from Algebraic Expressions

The greatest common factor (GCF) of an algebraic expression can sometimes be a binomial expression. Here is an example of a GCF that is a binomial.

Expressions with fractional or negative exponents can be factored by pulling out a GCF. Look for the variable or exponent that is common to each term of the expression and pull out that variable or exponent raised to the lowest power. These expressions follow the same factoring rules as those with integer exponents. For instance, [latex]2{x}^{\frac{1}{4}}+5{x}^{\frac{3}{4}}[/latex] can be factored by pulling out [latex]{x}^{\frac{1}{4}}[/latex] and being rewritten as [latex]{x}^{\frac{1}{4}}\left(2+5{x}^{\frac{1}{2}}\right)[/latex].