Finding the Antiderivative

Learning Outcomes

  • Find the general antiderivative of a given function
  • Explain the terms and notation used for an indefinite integral
  • State the power rule for integrals

We answer the first part of this question by defining antiderivatives. The antiderivative of a function [latex]f[/latex] is a function with a derivative [latex]f[/latex]. Why are we interested in antiderivatives? The need for antiderivatives arises in many situations, and we look at various examples throughout the remainder of the text. Here we examine one specific example that involves rectilinear motion. In our examination in Derivatives of rectilinear motion, we showed that given a position function [latex]s(t)[/latex] of an object, then its velocity function [latex]v(t)[/latex] is the derivative of [latex]s(t)[/latex]—that is, [latex]v(t)=s^{\prime}(t)[/latex]. Furthermore, the acceleration [latex]a(t)[/latex] is the derivative of the velocity [latex]v(t)[/latex]—that is, [latex]a(t)=v^{\prime}(t)=s^{\prime \prime}(t)[/latex]. Now suppose we are given an acceleration function [latex]a[/latex], but not the velocity function [latex]v[/latex] or the position function [latex]s[/latex]. Since [latex]a(t)=v^{\prime}(t)[/latex], determining the velocity function requires us to find an antiderivative of the acceleration function. Then, since [latex]v(t)=s^{\prime}(t)[/latex], determining the position function requires us to find an antiderivative of the velocity function. Rectilinear motion is just one case in which the need for antiderivatives arises. We will see many more examples throughout the remainder of the text. For now, let’s look at the terminology and notation for antiderivatives, and determine the antiderivatives for several types of functions. We examine various techniques for finding antiderivatives of more complicated functions in the second volume of this text (Introduction to Techniques of Integration).

The Reverse of Differentiation

At this point, we know how to find derivatives of various functions. We now ask the opposite question. Given a function [latex]f[/latex], how can we find a function with derivative [latex]f[/latex]? If we can find a function [latex]F[/latex] with derivative [latex]f[/latex], we call [latex]F[/latex] an antiderivative of [latex]f[/latex].

Definition

A function [latex]F[/latex] is an antiderivative of the function [latex]f[/latex] if

[latex]F^{\prime}(x)=f(x)[/latex]

 

for all [latex]x[/latex] in the domain of [latex]f[/latex].

Consider the function [latex]f(x)=2x[/latex]. Knowing the power rule of differentiation, we conclude that [latex]F(x)=x^2[/latex] is an antiderivative of [latex]f[/latex] since [latex]F^{\prime}(x)=2x[/latex]. Are there any other antiderivatives of [latex]f[/latex]? Yes; since the derivative of any constant [latex]C[/latex] is zero, [latex]x^2+C[/latex] is also an antiderivative of [latex]2x[/latex]. Therefore, [latex]x^2+5[/latex] and [latex]x^{2}-\sqrt{2}[/latex] are also antiderivatives. Are there any others that are not of the form [latex]x^2+C[/latex] for some constant [latex]C[/latex]? The answer is no. From Corollary 2 of the Mean Value Theorem, we know that if [latex]F[/latex] and [latex]G[/latex] are differentiable functions such that [latex]F^{\prime}(x)=G^{\prime}(x)[/latex], then [latex]F(x)-G(x)=C[/latex] for some constant [latex]C[/latex]. This fact leads to the following important theorem.

General Form of an Antiderivative

Let [latex]F[/latex] be an antiderivative of [latex]f[/latex] over an interval [latex]I[/latex]. Then,

  1. for each constant [latex]C[/latex], the function [latex]F(x)+C[/latex] is also an antiderivative of [latex]f[/latex] over [latex]I[/latex];
  2. if [latex]G[/latex] is an antiderivative of [latex]f[/latex] over [latex]I[/latex], there is a constant [latex]C[/latex] for which [latex]G(x)=F(x)+C[/latex] over [latex]I[/latex].

In other words, the most general form of the antiderivative of [latex]f[/latex] over [latex]I[/latex] is [latex]F(x)+C[/latex].

We use this fact and our knowledge of derivatives to find all the antiderivatives for several functions.

Example: Finding Antiderivatives

For each of the following functions, find all antiderivatives.

  1. [latex]f(x)=3x^2[/latex]
  2. [latex]f(x)=\dfrac{1}{x}[/latex]
  3. [latex]f(x)= \cos x[/latex]
  4. [latex]f(x)=e^x[/latex]

Watch the following video to see the worked solution to Example: Finding Antiderivatives.

Try It

Find all antiderivatives of [latex]f(x)= \sin x[/latex].

Try It

Indefinite Integrals

We now look at the formal notation used to represent antiderivatives and examine some of their properties. These properties allow us to find antiderivatives of more complicated functions. Given a function [latex]f[/latex], we use the notation [latex]f^{\prime}(x)[/latex] or [latex]\frac{df}{dx}[/latex] to denote the derivative of [latex]f[/latex]. Here we introduce notation for antiderivatives. If [latex]F[/latex] is an antiderivative of [latex]f[/latex], we say that [latex]F(x)+C[/latex] is the most general antiderivative of [latex]f[/latex] and write

[latex]\displaystyle\int f(x) dx=F(x)+C[/latex]

 

The symbol [latex]\displaystyle\int[/latex] is called an integral sign, and [latex]\displaystyle\int f(x) dx[/latex] is called the indefinite integral of [latex]f[/latex].

Definition

Given a function [latex]f[/latex], the indefinite integral of [latex]f[/latex], denoted

[latex]\displaystyle\int f(x) dx[/latex],

is the most general antiderivative of [latex]f[/latex]. If [latex]F[/latex] is an antiderivative of [latex]f[/latex], then

[latex]\displaystyle\int f(x) dx=F(x)+C[/latex]

The expression [latex]f(x)[/latex] is called the integrand and the variable [latex]x[/latex] is the variable of integration.

Given the terminology introduced in this definition, the act of finding the antiderivatives of a function [latex]f[/latex] is usually referred to as integrating [latex]f[/latex].

For a function [latex]f[/latex] and an antiderivative [latex]F[/latex], the functions [latex]F(x)+C[/latex], where [latex]C[/latex] is any real number, is often referred to as the family of antiderivatives of [latex]f[/latex]. For example, since [latex]x^2[/latex] is an antiderivative of [latex]2x[/latex] and any antiderivative of [latex]2x[/latex] is of the form [latex]x^2+C[/latex], we write

[latex]\displaystyle\int 2x dx=x^2+C[/latex]

 

The collection of all functions of the form [latex]x^2+C[/latex], where [latex]C[/latex] is any real number, is known as the family of antiderivatives of [latex]2x[/latex]. Figure 1 shows a graph of this family of antiderivatives.

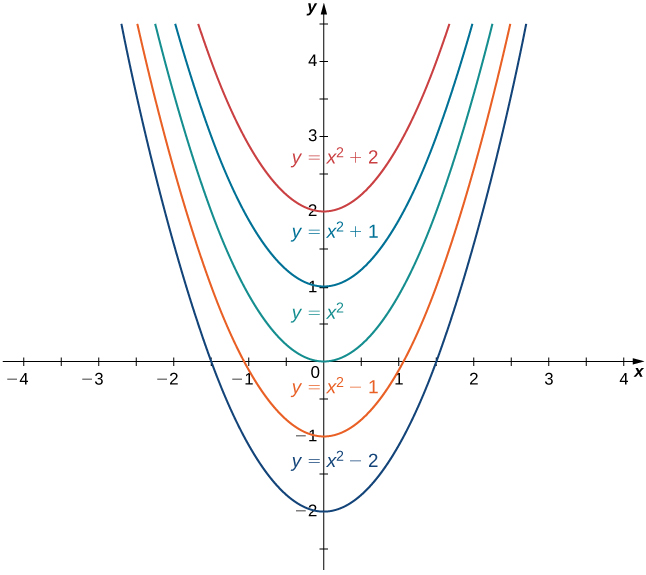
The graphs for y = x2 + 2, y = x2 + 1, y = x2, y = x2 − 1, and y = x2 − 2 are shown.

Figure 1. The family of antiderivatives of [latex]2x[/latex] consists of all functions of the form [latex]x^2+C[/latex], where [latex]C[/latex] is any real number.

For some functions, evaluating indefinite integrals follows directly from properties of derivatives. For example, for [latex]n \ne −1[/latex],

[latex]\displaystyle\int x^n dx=\dfrac{x^{n+1}}{n+1}+C[/latex],

 

which comes directly from

[latex]\frac{d}{dx}\left(\dfrac{x^{n+1}}{n+1}\right)=(n+1)\dfrac{x^n}{n+1}=x^n[/latex]

 

This fact is known as the power rule for integrals.

Power Rule for Integrals

For [latex]n \ne −1[/latex],

[latex]\displaystyle\int x^n dx=\dfrac{x^{n+1}}{n+1}+C[/latex]

 

Evaluating indefinite integrals for some other functions is also a straightforward calculation. The following table lists the indefinite integrals for several common functions. A more complete list appears in Appendix B: Table of Derivatives.

Integration Formulas
Differentiation Formula Indefinite Integral
[latex]\frac{d}{dx}(k)=0[/latex] [latex]\displaystyle\int kdx=\displaystyle\int kx^0 dx=kx+C[/latex]
[latex]\frac{d}{dx}(x^n)=nx^{n-1}[/latex] [latex]\displaystyle\int x^n dx=\frac{x^{n+1}}{n+1}+C[/latex] for [latex]n\ne −1[/latex]
[latex]\frac{d}{dx}(\ln |x|)=\frac{1}{x}[/latex] [latex]\displaystyle\int \frac{1}{x}dx=\ln |x|+C[/latex]
[latex]\frac{d}{dx}(e^x)=e^x[/latex] [latex]\displaystyle\int e^x dx=e^x+C[/latex]
[latex]\frac{d}{dx}(\sin x)= \cos x[/latex] [latex]\displaystyle\int \cos x dx= \sin x+C[/latex]
[latex]\frac{d}{dx}(\cos x)=− \sin x[/latex] [latex]\displaystyle\int \sin x dx=− \cos x+C[/latex]
[latex]\frac{d}{dx}(\tan x)= \sec^2 x[/latex] [latex]\displaystyle\int \sec^2 x dx= \tan x+C[/latex]
[latex]\frac{d}{dx}(\csc x)=−\csc x \cot x[/latex] [latex]\displaystyle\int \csc x \cot x dx=−\csc x+C[/latex]
[latex]\frac{d}{dx}(\sec x)= \sec x \tan x[/latex] [latex]\displaystyle\int \sec x \tan x dx= \sec x+C[/latex]
[latex]\frac{d}{dx}(\cot x)=−\csc^2 x[/latex] [latex]\displaystyle\int \csc^2 x dx=−\cot x+C[/latex]
[latex]\frac{d}{dx}( \sin^{-1} x)=\frac{1}{\sqrt{1-x^2}}[/latex] [latex]\displaystyle\int \frac{1}{\sqrt{1-x^2}} dx= \sin^{-1} x+C[/latex]
[latex]\frac{d}{dx}(\tan^{-1} x)=\frac{1}{1+x^2}[/latex] [latex]\displaystyle\int \frac{1}{1+x^2} dx= \tan^{-1} x+C[/latex]
[latex]\frac{d}{dx}(\sec^{-1} |x|)=\frac{1}{x\sqrt{x^2-1}}[/latex] [latex]\displaystyle\int \frac{1}{x\sqrt{x^2-1}} dx= \sec^{-1} |x|+C[/latex]

From the definition of indefinite integral of [latex]f[/latex], we know

[latex]\displaystyle\int f(x) dx=F(x)+C[/latex]

 

if and only if [latex]F[/latex] is an antiderivative of [latex]f[/latex]. Therefore, when claiming that

[latex]\displaystyle\int f(x) dx=F(x)+C[/latex]

 

it is important to check whether this statement is correct by verifying that [latex]F^{\prime}(x)=f(x)[/latex].

Example: Verifying an Indefinite Integral

Each of the following statements is of the form [latex]\displaystyle\int f(x) dx=F(x)+C[/latex]. Verify that each statement is correct by showing that [latex]F^{\prime}(x)=f(x)[/latex].

  1. [latex]\displaystyle\int (x+e^x) dx=\dfrac{x^2}{2}+e^x+C[/latex]
  2. [latex]\displaystyle\int xe^xdx=xe^x-e^x+C[/latex]

Try It

Verify that [latex]\displaystyle\int x \cos x dx=x \sin x+ \cos x+C[/latex].

Earlier, we listed the indefinite integrals for many elementary functions. Let’s now turn our attention to evaluating indefinite integrals for more complicated functions. For example, consider finding an antiderivative of a sum [latex]f+g[/latex]. In the last example. we showed that an antiderivative of the sum [latex]x+e^x[/latex] is given by the sum [latex](\frac{x^2}{2})+e^x[/latex]—that is, an antiderivative of a sum is given by a sum of antiderivatives. This result was not specific to this example. In general, if [latex]F[/latex] and [latex]G[/latex] are antiderivatives of any functions [latex]f[/latex] and [latex]g[/latex], respectively, then

[latex]\frac{d}{dx}(F(x)+G(x))=F^{\prime}(x)+G^{\prime}(x)=f(x)+g(x)[/latex]

 

Therefore, [latex]F(x)+G(x)[/latex] is an antiderivative of [latex]f(x)+g(x)[/latex] and we have

[latex]\displaystyle\int (f(x)+g(x)) dx=F(x)+G(x)+C[/latex]

 

Similarly,

[latex]\displaystyle\int (f(x)-g(x)) dx=F(x)-G(x)+C[/latex]

 

In addition, consider the task of finding an antiderivative of [latex]kf(x)[/latex], where [latex]k[/latex] is any real number. Since

[latex]\frac{d}{dx}(kf(x))=k\frac{d}{dx}F(x)=kF^{\prime}(x)[/latex]

 

for any real number [latex]k[/latex], we conclude that

[latex]\displaystyle\int kf(x) dx=kF(x)+C[/latex]

 

These properties are summarized next.

Properties of Indefinite Integrals

Let [latex]F[/latex] and [latex]G[/latex] be antiderivatives of [latex]f[/latex] and [latex]g[/latex], respectively, and let [latex]k[/latex] be any real number.

 

Sums and Differences

[latex]\displaystyle\int (f(x) \pm g(x)) dx=F(x) \pm G(x)+C[/latex]

 

Constant Multiples

[latex]\displaystyle\int kf(x) dx=kF(x)+C[/latex]

From this theorem, we can evaluate any integral involving a sum, difference, or constant multiple of functions with antiderivatives that are known. Evaluating integrals involving products, quotients, or compositions is more complicated (see the previous example). for an example involving an antiderivative of a product.) We look at and address integrals involving these more complicated functions in Introduction to Integration. In the next example, we examine how to use this theorem to calculate the indefinite integrals of several functions.

Example: Evaluating Indefinite Integrals

Evaluate each of the following indefinite integrals:

  1. [latex]\displaystyle\int (5x^3-7x^2+3x+4) dx[/latex]
  2. [latex]\displaystyle\int \frac{x^2+4\sqrt[3]{x}}{x} dx[/latex]
  3. [latex]\displaystyle\int \frac{4}{1+x^2} dx[/latex]
  4. [latex]\displaystyle\int \tan x \cos x dx[/latex]

Watch the following video to see the worked solution to Example: Evaluating Indefinite Integrals.

Try It

Evaluate [latex]\displaystyle\int (4x^3-5x^2+x-7) dx[/latex]

Try It

Try It