Learning Outcomes
- Calculate the partial derivatives of a function of two variables.
- Calculate the partial derivatives of a function of more than two variables.
Derivatives of a Function of Two Variables
When studying derivatives of functions of one variable, we found that one interpretation of the derivative is an instantaneous rate of change of [latex]y[/latex] as a function of [latex]x[/latex]. Leibniz notation for the derivative is [latex]dy/dx[/latex], which implies that [latex]y[/latex] is the dependent variable and [latex]x[/latex] is the independent variable. For a function [latex]z=f\,(x,\ y)[/latex] of two variables, [latex]x[/latex] and [latex]y[/latex] are the independent variables and [latex]z[/latex] is the dependent variable. This raises two questions right away: How do we adapt Leibniz notation for functions of two variables? Also, what is an interpretation of the derivative? The answer lies in partial derivatives.
Definition
Let [latex]f\,(x,\ y)[/latex] be a function fo two variables. Then the partial derivative of [latex]f[/latex] with respect to [latex]x[/latex], written as [latex]\partial f/\partial x[/latex], or [latex]f_x[/latex], is defined as
[latex]\large{\frac{\partial f}{\partial x}=\lim_{h\to{0}}\frac{f\,(x+h,\ y)-f\,(x,\ y)}{h}}[/latex].
The partial derivative of [latex]f[/latex] with respect to [latex]y[/latex], written as [latex]\partial f/\partial y[/latex], or [latex]f_y[/latex], is defined as
[latex]\large{\frac{\partial f}{\partial y}=\lim_{k\to{0}}\frac{f\,(x,\ y+k)-f\,(x,\ y)}{k}}[/latex].
This definition shows two differences already. First, the notation changes, in the sense that we still use a version of Leibniz notation, but the [latex]d[/latex] in the original notation is replaced with the symbol [latex]\partial[/latex]. (This rounded “[latex]d[/latex]” is usually called “partial,” so [latex]\partial f/\partial x[/latex] is spoken as the “partial of [latex]f[/latex] with respect to [latex]x[/latex].”) This is the first hint that we are dealing with partial derivatives. Second, we now have two different derivatives we can take, since there are two different independent variables. Depending on which variable we choose, we can come up with different partial derivatives altogether, and often do.
Example: Calculating Partial Derivatives from the Definition
Use the definition of the partial derivative as a limit to calculate [latex]\partial f/\partial x[/latex] and [latex]\partial f/\partial y[/latex] for the function
[latex]f\,(x,\ y)=x^{2}-3xy+2y^{2}-4x+5y-12[/latex].
Show Solution
First, calculate [latex]f\,(x+h,\ y)[/latex].
[latex]\begin{array}{ccc}\hfill {f\,(x+h,\ y)} & =\hfill & {(x+h)^{2}-3(x+h)y+2y^{2}-4(x+h)+5y-12} \hfill \\ \hfill & =\hfill & {x^{2}+2xh+h^{2}-3xy-3hy+2y^{2}-4x-4h+5y-12.} \hfill \\ \hfill \end{array}[/latex]
Next, substitute this into our definition and simplify:
[latex]\begin{array}{ccc}\hfill {\frac{\partial f}{\partial x}} & =\hfill & {\displaystyle\lim_{h\to 0}\frac{f\,(x+h,\ y)-f\,(x,\ y)}{h}} \hfill \\ \hfill & =\hfill & {\displaystyle\lim_{h\to 0}\frac{(x^{2}+2xh+h^{2}-3xy-3hy+2y^{2}-4x-4h+5y-12)-(x^{2}-3xy+2y^{2}-4x+5y-12)}{h}} \hfill \\ \hfill & =\hfill & {\displaystyle\lim_{h\to 0}\frac{x^{2}+2xh+h^{2}-3xy-3hy+2y^{2}-4x-4h+5y-12-x^{2}+3xy-2y^{2}+4x-5y+12}{h}}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{h\to 0}\frac{2xh+h^{2}-3hy-4h}{h}}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{h\to 0}\frac{h(2x+h-3y-4)}{h}}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{h\to 0}(2x+h-3y-4)}\hfill \\ \hfill & =\hfill & {2x-3y-4}\hfill \\ \hfill \end{array}[/latex]
To calculate [latex]\frac{\partial f}{\partial y}[/latex], first calculate [latex]f\,(x,\ y+h)[/latex]:
[latex]\begin{array}{ccc}\hfill {f\,(x,\ y+h)} & =\hfill & {x^{2}-3x(y+h)+2(y+h)^{2}-4x+5(y+h)-12}\hfill \\ \hfill & =\hfill & {x^{2}-3xy-3xh+2y^{2}+4yh+2h^{2}-4x+5y+5h-12.}\hfill \\ \hfill \end{array}[/latex]
Next, substitute this into our definition and simplify:
[latex]\begin{array}{ccc}\hfill {\frac{\partial f}{\partial y}} & =\hfill & {\displaystyle\lim_{k\to 0}\frac{f\,(x,\ y+h)-f\,(x,\ y)}{k}}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{k\to 0}\frac{(x^{2}-3xy-3xh+2y^{2}+4yh+2h^{2}-4x+5y+5h-12)-(x^{2}-3xy+2y^{2}-4x+5y-12)}{k}}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{k\to 0}\frac{x^{2}-3xy-3xh+2y^{2}+4yh+2h^{2}-4x+5y+5h-12-x^{2}+3xy-2y^{2}+4x-5y+12}{k}}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{k\to 0}\frac{-3xk+4yk+2k^{2}+5k}{k}}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{k\to 0}\frac{h(-3x+4y+2k+5)}{k}}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{k\to 0}(-3x+4y+2k+5)}\hfill \\ \hfill & =\hfill & {-3x+4y+5.} \hfill \\ \hfill \end{array}[/latex]
TRY IT
Use the definition of the partial derivative as a limit to calculate [latex]\partial f/\partial x[/latex] and [latex]\partial f/\partial y[/latex] for the function
[latex]f\,(x,\ y)=4x^{2}+2xy-y^{2}+3x-2y+5.[/latex]
Show Solution
[latex]\frac{\partial f}{\partial x}=8x+2y+3,\ \frac{\partial f}{\partial y}=2x-2y-2[/latex]
The idea to keep in mind when calculating partial derivatives is to treat all independent variables, other than the variable with respect to which we are differentiating, as constants. Then proceed to differentiate as with a function of a single variable. To see why this is true, first fix [latex]y[/latex] and define [latex]g\,(x)=f\,(x,\ y)[/latex] as a function of [latex]x[/latex]. Then
[latex]g'\,(x)=\displaystyle\lim_{h\to 0}\frac{g\,(x+h)-g\,(x)}{h}=\displaystyle\lim_{h\to 0}\frac{f\,(x+h,\ y)-f\,(x,\ y)}{h}=\frac{\partial f}{\partial x}.[/latex]
The same is true for calculating the partial derivative of [latex]f[/latex] with respect to [latex]y[/latex]. This time, fix [latex]x[/latex] and define [latex]h\,(y)=f\,(x,\ y)[/latex] as a function of [latex]y.[/latex] Then
[latex]h'\,(x)=\displaystyle\lim_{k\to 0}\frac{h\,(x+h)-h\,(x)}{k}=\displaystyle\lim_{k\to 0}\frac{f\,(x,\ y+k)-f\,(x,\ y)}{k}=\frac{\partial f}{\partial y}.[/latex]
All differentiation rules from the Introduction to Derivatives apply.
Example: Calculating Partial Derivatives
Calculate [latex]\partial f/\partial x[/latex] and [latex]\partial f/\partial y[/latex] for the following functions by holding the opposite variable constant then differentiating:
- [latex]f\,(x,\ y)=x^{2}-3xy+2y^{2}-4x+5y-12[/latex].
- [latex]g\,(x,\ y)=\sin{(x^{2}y-2x+4)}[/latex]
Show Solution
- To calculate [latex]\partial f/\partial x[/latex], treat the variable [latex]y[/latex] as a constant. Then differentiate [latex]f\,(x,\ y)[/latex] with respect to [latex]x[/latex] using the sum, difference, and power rules:
[latex]\begin{array}{ccc}\hfill {\frac{\partial f}{\partial x}} & =\hfill & {\frac{\partial}{\partial x}\big[x^{2}-3xy+2y^{2}-4x+5y-12\big]}\hfill \\ \hfill & =\hfill & {\frac{\partial}{\partial x}\big[x^{2}\big]-\frac{\partial}{\partial x}\big[3xy\big]+\frac{\partial}{\partial x}\big[2y^{2}\big]-\frac{\partial}{\partial x}\big[4x\big]+\frac{\partial}{\partial x}\big[5y\big]-\frac{\partial}{\partial x}\big[12\big]}\hfill \\ \hfill & =\hfill & {2x-3y+0-4+0-0}\hfill \\ \hfill & =\hfill & {2x-3y-4.} \hfill \\ \hfill \end{array}[/latex]
The derivatives of the third, fifth, and sixth terms are all zero because they do not contain the variable [latex]x[/latex], so they are treated as constant terms. The derivative of the second term is equal to the coefficient of [latex]x[/latex], which is [latex]-3y[/latex]. Calculating [latex]\partial f/\partial y[/latex]:
[latex]\begin{array}{ccc}\hfill {\frac{\partial f}{\partial y}} & =\hfill & {\frac{\partial}{\partial y}\big[x^{2}-3xy+2y^{2}-4x+5y-12\big]}\hfill \\ \hfill & =\hfill & {\frac{\partial}{\partial y}\big[x^{2}\big]-\frac{\partial}{\partial y}\big[3xy\big]+\frac{\partial}{\partial y}\big[2y^{2}\big]-\frac{\partial}{\partial y}\big[4x\big]+\frac{\partial}{\partial y}\big[5y\big]-\frac{\partial}{\partial y}\big[12\big]}\hfill \\ \hfill & =\hfill & {-3x+4y-0+5-0}\hfill \\ \hfill & =\hfill & {-3x+4y+5.} \hfill \\ \hfill \end{array}[/latex]
These are the same answers obtained in the previous example
- To calculate [latex]\partial g/\partial x[/latex], create the variable [latex]y[/latex] as a constant. Then differentiate [latex]g\,(x,\ y)[/latex] with respect to [latex]x[/latex] using the chain rule and power rule:
[latex]\begin{array}{ccc}\hfill{\frac{\partial g}{\partial y}} & =\hfill & {\frac{\partial}{\partial x}\big[\sin{(x^{2}y-2x+4)}\big]} \hfill \\ \hfill & =\hfill & {\cos{(x^{2}y-2x+4)}\frac{\partial}{\partial x}[x^{2}y-2x+4]}\hfill \\ \hfill & =\hfill & {(2xy-2)\cos{(x^{2}y-2x+4)}.}\hfill \\ \hfill \end{array}[/latex]
To calculate [latex]\partial f/\partial y[/latex], treat the variable [latex]x[/latex] as a constant. Then differentiate [latex]g\,(x,\ y)[/latex] with respect to [latex]y[/latex] using the chain rule and power rule:
[latex]\begin{array}{ccc}\hfill {\frac{\partial g}{\partial y}} & =\hfill & {\frac{\partial}{\partial y}\big[\sin{(x^{2}y-2x+4)}\big]}\hfill \\ \hfill & =\hfill & {\cos{(x^{2}y-2x+4)}\frac{\partial}{\partial x}[x^{2}y-2x+4]} \hfill \\ \hfill & =\hfill & {x^{2}\cos{(x^{2}-2x+4)}.}\hfill \\ \hfill \end{array}[/latex]
TRY IT
Calculate [latex]\partial f/\partial x[/latex] and [latex]\partial f/\partial y[/latex] for the function [latex]f\,(x,\ y)=\tan{(x^{3}-3x^{2}y^{2}+2y^{4})}[/latex] by holding the opposite variable constant, then differentiating.
Show Solution
[latex]\frac{\partial f}{\partial x}=(3x^{2}-6xy^{2})\sec^{2}{(x^{3}-3x^{2}y^{2}+2y^{4})}[/latex]
[latex]\frac{\partial f}{\partial y}=(-6x^{2}y+8y^{3})\sec^{2}{(x^{3}-3x^{2}y^{2}+2y^{4})}[/latex]
Watch the following video to see the worked solution to the above Try It
How can we interpret these partial derivatives? Recall that the graph of a function of two variables is a surface in [latex]\mathbb{R}^{3}[/latex]. If we remove the limit from the definition of the partial derivative with respect to [latex]x[/latex], the difference quotient remains:
[latex]\LARGE{\frac{f\,(x+h,\ y)-f\,(x,\ y)}{h}}[/latex].
This resembles the difference quotient for the derivative of a function of one variable, except for the presence of the [latex]y[/latex] variable. variable. Figure 1 illustrates a surface described by an arbitrary function [latex]z=f\,(x,\ y)[/latex].
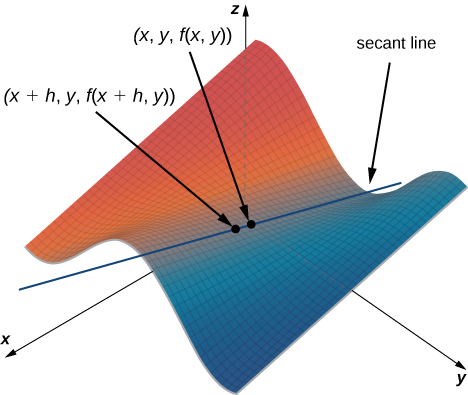
Figure 1. Secant line passing through the points [latex]\small{(x,y,f(x,y))}[/latex] and [latex]\small{(x+h,y,f(x+h,y))}[/latex].
In Figure 1, the value of [latex]h[/latex] is positive. If we graph [latex]f\,(x,\ y)[/latex] and [latex]f\,(x+h,\ y)[/latex] for an arbitrary point [latex](x,\ y)[/latex], then the slope of the secant line passing through these two points is given by
[latex]\LARGE{\frac{f\,(x+h,\ y)-f\,(x,\ y)}{h}}[/latex].
This line is parallel to the [latex]x[/latex]-axis. Therefore, the slope of the secant line represents an average rate of change of the function [latex]f[/latex] as we travel parallel to the [latex]x[/latex]-axis. As [latex]h[/latex] approaches zero, the slope of the secant line approaches the slope of the tangent line.
If we chose to change [latex]y[/latex] instead of [latex]x[/latex] by the same incremental value [latex]h[/latex], then the secant line is parallel to the [latex]y[/latex]-axisw and so is the tangent line. Therefore, [latex]\partial f/\partial x[/latex] represents the slope of the tangent line passing through the point [latex](x,\ y,\ f\,(x,\ y))[/latex] parallel to the [latex]x[/latex]-axis and [latex]\partial f/\partial y[/latex] represents the slope of the tangent line passing through the point [latex](x,\ y,\ f\,(x,\ y))[/latex] parallel to the [latex]y[/latex]-axis. If we wish to find the slope of a tangent line passing through the same point in any other direction, then we need what are called directional derivatives, which we discuss in Directional Derivatives and the Gradient.
We now return to the idea of contour maps, which we introduced in Functions of Several Variables. We can use a contour map to estimate partial derivatives of a function [latex]g\,(x,\ y)[/latex].
Example: Partial DErivatives from a Contour Map
Use a contour map to estimate [latex]\partial g/\partial x[/latex] at the point [latex](\sqrt{5},\ 0)[/latex] for the function
[latex]g\,(x,\ y)=\sqrt{9-x^{2}-y^{2}}[/latex].
Show Solution
The following graph represents a contour map for the function [latex]g\,(x,\ y)=\sqrt{9-x^{2}-y^{2}}[/latex].

Figure 2. Contour map for the function [latex]\small{g(x,y)=\sqrt{9-x^{2}-y^{2}}}[/latex], using [latex]\small{c=0,1,2}[/latex], and [latex]\small{3}[/latex] ([latex]\small{c=3}[/latex] corresponds to the origin).
The inner circle on the contour map corresponds to [latex]c=2[/latex] and the next circle out corresponds to [latex]c=1[/latex]. The first circle is given by the equation [latex]2=\sqrt{9-x^{2}-y^{2}}[/latex]; the second circle is given by the equation [latex]1=\sqrt{9-x^{2}-y^{2}}[/latex]. The first equation simplifies to [latex]x^{2}+y^{2}=5[/latex] and the second equation simplifies to [latex]x^{2}+y^{2}=8[/latex]. The [latex]x[/latex]-intercept of the first circle is [latex](\sqrt{5},\ 0)[/latex] and the [latex]x[/latex]-intercept of the second circle is [latex](2\sqrt{2},\ 0)[/latex]. We can estimate the value of [latex]\partial g/\partial x[/latex] evaluated at the point [latex](\sqrt{5},\ 0)[/latex] using the slope formula:
[latex]\large{\frac{\partial g}{\partial x}\bigg|_{(x,\ y)=(\sqrt{5},\ 0)}\approx\frac{g\,(\sqrt{5},\ 0)-g\,(2\sqrt{2},\ 0)}{\sqrt{5}-2\sqrt{2}}=\frac{2-1}{\sqrt{5}-2\sqrt{2}}=\frac{1}{\sqrt{5}-2\sqrt{2}}\approx -1.688.}[/latex]
To calculate the exact value of [latex]\partial g/\partial x[/latex] evaluated at the point [latex](\sqrt{5},\ 0)[/latex], we start by finding [latex]\partial g/\partial x[/latex] using the chain rule. First, we rewrite the function as [latex]g\,(x,\ y)=\sqrt{9-x^{2}-y^{2}}=(9-x^{2}-y^{2})^{\frac{1}{2}}[/latex] and then differentiate with respect to [latex]x[/latex] while holding [latex]y[/latex] constant:
[latex]\large{\frac{\partial g}{\partial x}=\frac{1}{2}(9-x^{2}-y^{2})^{-\frac{1}{2}}(-2x)=-\frac{x}{\sqrt{9-x^{2}-y^{2}}}.}[/latex]
Next, we evaluate this expression using [latex]x=\sqrt{5}[/latex] and [latex]y=0[/latex]:
[latex]\large{\frac{\partial g}{\partial x}\bigg|_{(x,\ y)=(\sqrt{5},\ 0)}=-\frac{\sqrt{5}}{\sqrt{9-(\sqrt{5})^{2}-(0)^{2}}}=-\frac{\sqrt{5}}{\sqrt{4}}=-\frac{\sqrt{5}}{2}\approx -1.118.}[/latex]
The estimate for the partial derivative corresponds to the slope of the secant line passing through the points [latex](\sqrt{5},\ 0,\ g\,(\sqrt{5},\ 0))[/latex] and [latex](2\sqrt{2},\ 0,\ g\,(2\sqrt{2},\ 0))[/latex]. It represents an approximation to the slope of the tangent line to the surface through the point [latex](\sqrt{5},\ 0,\ g\,(\sqrt{5},\ 0))[/latex], which is parallel to the [latex]x[/latex]-axis.
TRY IT
Use a contour map to estimate [latex]\partial f/\partial y[/latex] at point [latex](0,\ \sqrt{2})[/latex] for the function
[latex]f\,(x,\ y)=x^{2}-y^{2}[/latex].
Compare this with the exact answer.
Show Solution
Using the curves corresponding to [latex]c=-2[/latex] and [latex]c=-3[/latex], we obtain
[latex]\large{\frac{\partial f}{\partial y}\bigg|_{(x,\ y)=(0,\ \sqrt{2})}\approx\frac{f\,(0,\ \sqrt{3})-f\,(0,\ \sqrt{2})}{\sqrt{3}-\sqrt{2}}=\frac{-3-(-2)}{\sqrt{3}-\sqrt{2}}\cdot\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}=-\sqrt{3}-\sqrt{2}\approx-3.146}[/latex].
The exact answer is
[latex]\large{\frac{\partial f}{\partial y}\bigg|_{(x,\ y)(0,\ \sqrt{2}}=-2y\big|_{(x,\ y)=(0,\ \sqrt{2})}=-2\sqrt{2}\approx -2.828.}[/latex]
Functions of More Than Two Variables
Suppose we have a function of three variables, such as [latex]w=f\,(x,\ y,\ z)[/latex]. We can calculate partial derivatives of [latex]w[/latex] with respect to any of the independent variables, simply as extensions of the definitions for partial derivatives of functions of two variables.
Definition
Let [latex]f\,(x,\ y,\ z)[/latex] be a function of three variables. Then, the partial derivative of [latex]f[/latex] with respect to [latex]x[/latex], written as [latex]\partial f/\partial x[/latex], or [latex]f_x[/latex], is defined to be
[latex]\large{\frac{\partial f}{\partial x}=\displaystyle\lim_{h\to 0}\frac{f\,(x+h,\ y,\ z)-f\,(x,\ y,\ z)}{h}}[/latex].
The partial derivative of [latex]f[/latex] with respect to [latex]y[/latex], written as [latex]\partial f/\partial y[/latex], or [latex]f_y[/latex], is defined to be
[latex]\large{\frac{\partial f}{\partial y}=\displaystyle\lim_{k\to 0}\frac{f\,(x,\ y+k,\ z)-f\,(x,\ y,\ z)}{k}}[/latex].
The partial derivative of [latex]f[/latex] with respect to [latex]z[/latex], written as [latex]\partial f/\partial z[/latex], or [latex]f_z[/latex], is defined to be
[latex]\large{\frac{\partial f}{\partial z}=\displaystyle\lim_{m\to 0}\frac{f\,(x,\ y,\ z+m)-f\,(x,\ y,\ z)}{m}}[/latex].
We can calculate a partial derivative of a function of three variables using the same idea we used for a function of two variables. Fore example, if we have a function [latex]f[/latex] of [latex]x,\ y[/latex], and [latex]z[/latex], and we wish to calculate [latex]\partial f/\partial x[/latex], then we create the other two independent variables as if they are constants, then differentiate with respect to [latex]x[/latex].
Example: Calculating partial derivatives for a Function of Three Variables
Use the limit definition of partial derivatives to calculate [latex]\partial f/\partial x[/latex] for the function
[latex]\large{f\,(x,\ y,\ z)=x^{2}-3xy+2y^{2}-4xz+5yz^{2}-12x+4y-3z}[/latex].
Then, find [latex]\partial f/\partial y[/latex] and [latex]\partial f/\partial z[/latex] by setting the other two variables constant and differentiating accordingly.
Show Solution
We first calculate [latex]\partial f/\partial x[/latex] using our definition, then we calculate the other two partial derivatives by holding the remaining variables constant. To use the equation to find [latex]\partial f/\partial x[/latex], we first need to calculate [latex]f\,(x+h,\ y,\ z)[/latex]:
[latex]\begin{array}{ccc}\hfill {f\,(x+h,\ y,\ z)} & =\hfill & {(x+h)^{2}-3(x+h)y+2y^{2}-4(x+h)z+5yz^{2}-12(x+h)+4y-3z}\hfill \\ \hfill & =\hfill & {x^{2}+2xh+h^{2}-3xy-3xh+2y^{2}-4xz-4hz+5yz^{2}-12x-12h+4y-3z} \hfill \\ \hfill \end{array}[/latex]
and recall that [latex]f\,(x,\ y,\ z)=x^{2}-3xy+2y^{2}-4xz+5yz^{2}-12x+4y-3z[/latex]. Next, we substitute these two expressions into the equation:
[latex]\begin{array}{ccc}\hfill {\frac{\partial f}{\partial x}} & =\hfill & {\displaystyle\lim_{h\to 0}\left[\frac{x^{2}+2xh+h^{2}-3xy-3xh+2y^{2}-4xz-4hz+5yz^{2}-12x-12h+4y-3z}{h} \\ - \frac{x^{2}-3xy+2y^{2}-4xz+5yz^{2}-12x+4y-3z}{h}\right]}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{h\to 0}\left[\frac{2xh+h^{2}-3hy-4hz-12h}{h}\right]}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{h\to 0}\left[\frac{h(2x+h-3y-4z-12)}{h}\right]}\hfill \\ \hfill & =\hfill & {\displaystyle\lim_{h\to 0}(2x+h-3y-4z-12)}\hfill \\ \hfill & =\hfill & {2x-3y-4z-12.} \hfill \\ \hfill \end{array}[/latex]
Then we find [latex]\partial f/\partial y[/latex] by holding [latex]x[/latex] and [latex]z[/latex] constant. Therefore, any term that does not include the variable [latex]y[/latex] is constant, and its derivative is zero. We can apply the sum, difference, and power rules for functions of one variable:
[latex]\begin{alignat}{2} &\frac{\partial}{\partial y}\left[x^{2}-3xy+2y^{2}-4xz+5yz^{2}-12x+4y-3z\right] \\ \hspace{2cm}&=\frac{\partial}{\partial y}\left[x^{2}\right]-\frac{\partial}{\partial y}\left[3xy\right]+\frac{\partial}{\partial y}\left[2y^{2}\right]-\frac{\partial}{\partial y}\left[4xz\right]+\frac{\partial}{\partial y}\left[5yz^{2}\right]-\frac{\partial}{\partial y}\left[12x\right]+\frac{\partial}{\partial y}\left[4y\right]-\frac{\partial}{\partial y}\left[3z\right] &\quad\\ &=0-3x+4y-0+5z^2-0+4-0\\ &=-3x+4y+5z^2+4.\\ \end{alignat}[/latex]
To calculate [latex]\partial f/\partial z[/latex], we hold [latex]x[/latex] and [latex]y[/latex] constant and apply the sum, difference, and power rules for functions of one variable:
[latex]\begin{alignat}{2} &\frac{\partial}{\partial z}\left[x^{2}-3xy+2y^{2}-4xz+5yz^{2}-12x+4y-3z\right] \\ \hspace{2cm}&=\frac{\partial}{\partial z}\left[x^{2}\right]-\frac{\partial}{\partial z}\left[3xy\right]+\frac{\partial}{\partial z}\left[2y^{2}\right]-\frac{\partial}{\partial z}\left[4xz\right]+\frac{\partial}{\partial z}\left[5yz^{2}\right]-\frac{\partial}{\partial z}\left[12x\right]+\frac{\partial}{\partial z}\left[4y\right]-\frac{\partial}{\partial y}\left[3z\right] &\quad\\ &=0-0+0-4x+10yz-0+0-3\\ &=-4z+10yz-3.\\ \end{alignat}[/latex]
TRY IT
Use the limit definition of partial derivatives to calculate [latex]\partial f/\partial x[/latex] for the function
[latex]f\,(x,\ y,\ z)=2x^{2}-4x^{2}+2y^{2}+5xz^{2}-6x+3z-8[/latex].
Then, find [latex]\partial f/\partial y[/latex] and [latex]\partial f/\partial z[/latex] by setting the other two variables constant and differentiating accordingly.
Show Solution
[latex]\begin{alignat}{2} \hspace{5cm} \frac{\partial f}{\partial x}&=4x-8xy+5z^{2}-6 \\ \frac{\partial f}{\partial y}& = -4x^{2}+4y&\quad\\ \frac{\partial f}{\partial z}& =10xz+3\\ \end{alignat}[/latex]
Example: Calculating Partial Derivatives for a Function of Three Variables
Calculate the three partial derivatives of the following functions.
- [latex]f\,(x,\ y,\ z)=\frac{x^{2}y-4xz+y^{2}}{x-3yz}[/latex]
- [latex]g\,(x,\ y,\ z)=\sin{(x^{2}y-z)}+\cos{(x^{2}-yz)}[/latex]
Show Solution
In each case, treat all variables as constants except the one whose partial derivative you are calculating.
[latex]\begin{array}{ccc}1. \hspace{1cm} {\frac{\partial f}{\partial x}} & =\hfill & {\frac{\partial}{\partial x}\bigg[\frac{x^{2}y-4xz+y^{2}}{x-3yz}\bigg]}\hfill \\ \hfill & =\hfill & {\frac{\frac{\partial}{\partial x}(x^{2}y-4xz+y^{2})(x-3yz)-(x^{2}y-4xz+y^{2})\frac{\partial}{\partial x}(x-3yz)}{(x-3yz)^{2}}}\hfill \\ \hfill & =\hfill & {\frac{(2xy-4z)(x-3yz)-(x^{2}y-4xz+y^{2})(1)}{(x-3yz)^{2}}}\hfill \\ \hfill & =\hfill & {\frac{2x^{2}y-6xy^{2}z-4xz+12yz^{2}-x^{2}y+4xz-y^{2}}{(x-3yz)^{2}}} \hfill \\ \hfill & =\hfill & {\frac{x^{2}y-6xy^{2}z-4xz+12yz^{2}+4xz-y^{2}}{(x-3yz)^{2}}}\hfill \\ \hfill {\frac{\partial f}{\partial y}} & =\hfill & {\frac{\partial}{\partial y}\bigg[\frac{x^{2}y-4xz+y^{2}}{x-3yz}\bigg]}\hfill \\ \hfill & =\hfill & {\frac{\frac{\partial}{\partial y}(x^{2}y-4xz+y^{2})(x-3yz)-(x^{2}y-4xz+y^{2})\frac{\partial}{\partial y}(x-3yz)}{(x-3yz)^{2}}}\hfill \\ \hfill & =\hfill & {\frac{(x^{2}+2y)(x-3yz)-(x^{2}y-4xz+y^{2})(-3z)}{(x-3yz)^{2}}}\hfill \\ \hfill & =\hfill & {\frac{x^{3}-3x^{2}yz+2xy-6y^{2}z+3x^{2}yz-12xz^{2}+3y^{2}z}{(x-3yz)^{2}}}\hfill \\ \hfill & =\hfill & {\frac{x^{3}+2xy-3y^{2}z-12xz^{2}}{(x-3yz)^{2}}}\hfill \\ \hfill {\frac{\partial f}{\partial z}} & =\hfill & {\frac{\partial}{\partial z}\bigg[\frac{x^{2}y-4xz+y^{2}}{x-3yz}\bigg]}\hfill \\ \hfill & =\hfill & {\frac{\frac{\partial}{\partial z}(x^{2}y-4xz+y^{2})(x-3yz)-(x^{2}y-4xz+y^{2})\frac{\partial}{\partial z}(x-3yz)}{(x-3yz)^{2}}} \hfill \\ \hfill & =\hfill & {\frac{(-4x)(x-3yz)-(x^{2}y-4xz+y^{2})(-3y)}{(x-3yz)^{2}}} \hfill \\ \hfill & =\hfill & {\frac{-4x^{2}+12xyz+3x^{2}y^{2}-12xyz+3y^{3}}{(x-3yz)^{2}}}\hfill \\ \hfill & =\hfill & {\frac{-4x^{2}+3x^{2}y^{2}+3y^{3}}{(x-3yz)^{2}}} \hfill \\ \hfill \end{array}[/latex]
[latex]\begin{array}{ccc}2. \hspace{1cm} {\frac{\partial f}{\partial x}} & =\hfill & {\frac{\partial}{\partial x}\left[\sin{(x^{2}y-z)}+\cos{(x^{2}-yz)}\right]}\hfill \\ \hfill & =\hfill & {(\cos{(x^{2}y-z)})\frac{\partial}{\partial x}(x^{2}y-z)-(\sin{(x^{2}-yz)})\frac{\partial}{\partial x}(x^{2}-yz)}\hfill \\ \hfill & =\hfill & {2xy\cos{(x^{2}y-z)}-2x\sin{(x^{2}-yz)}} \hfill \\ \hfill {\frac{\partial f}{\partial y}} & =\hfill & {\frac{\partial}{\partial y}\left[\sin{(x^{2}y-z)}+\cos{(x^{2}-yz)}\right]}\hfill \\ \hfill & =\hfill & {(\cos{(x^{2}y-z)})\frac{\partial}{\partial y}(x^{2}y-z)-(\sin{(x^{2}-yz)})\frac{\partial}{\partial y}(x^{2}-yz)}\hfill \\ \hfill & =\hfill & {x^{2}\cos{(x^{2}y-z)}+z\sin{(x^{2}-yz)}} \hfill \\ \hfill {\frac{\partial f}{\partial z}} & =\hfill & {\frac{\partial}{\partial z}\left[\sin{(x^{2}y-z)}+\cos{(x^{2}-yz)}\right]}\hfill \\ \hfill & =\hfill & {(\cos{(x^{2}y-z)})\frac{\partial}{\partial z}(x^{2}y-z)-(\sin{(x^{2}-yz)})\frac{\partial}{\partial z}(x^{2}-yz)} \hfill \\ \hfill & =\hfill & {-\cos{(x^{2}y-z)}+y\sin{(x^{2}-yz)}} \hfill \\ \hfill \end{array}[/latex]
TRY IT
Calculate [latex]\partial f/\partial x,\ \partial f/\partial y[/latex], and [latex]\partial f/\partial z[/latex] for the function [latex]f\,(x,\ y,\ z)=\sec{(x^{2}y)}-\tan{(x^{3}yz^{2}})[/latex].
Show Solution
[latex]\begin{alignat}{2} \hspace{5cm} \frac{\partial f}{\partial x}&=2xy\sec{(x^{2}y)}\tan{(x^{2}y)}-3x^{2}yz^{2}\sec^{2}{(x^{3}yz^{2})} \\ \frac{\partial f}{\partial y}&=x^{2}\sec{(x^{2}y)}\tan{(x^{2}y)-x^{3}z^{2}}\sec^{2}{(x^{3}yz^{2})}&\quad\\ \frac{\partial f}{\partial z}&=-2x^{3}yz\sec^{2}{(x^{3}yz^{2})}\\ \end{alignat}[/latex]
Watch the following video to see the worked solution to the above Try It
Candela Citations
CC licensed content, Original
CC licensed content, Shared previously


