Learning Objectives
- Determine the directional derivative in a given direction for a function of two variables.
We start with the graph of a surface defined by the equation [latex]z=f(x, y)[/latex]. Given a point [latex](a, b)[/latex] in the domain of [latex]f[/latex], we choose a direction to travel from that point. We measure the direction using an angle [latex]\theta[/latex] which is measured counterclockwise in the [latex]x, y[/latex]-plane, starting at zero from the positive [latex]x[/latex]-axis (Figure 1). The distance we travel is [latex]h[/latex] and the direction we travel is given by the unit vector [latex]{\bf{u}}=(\cos\theta){\bf{i}}+(\sin\theta)\bf{j}[/latex]. Therefore, the [latex]z[/latex]-coordinate of the second point on the graph is given by [latex]z=f(a+h\cos\theta,\,b+h\sin\theta)[/latex].
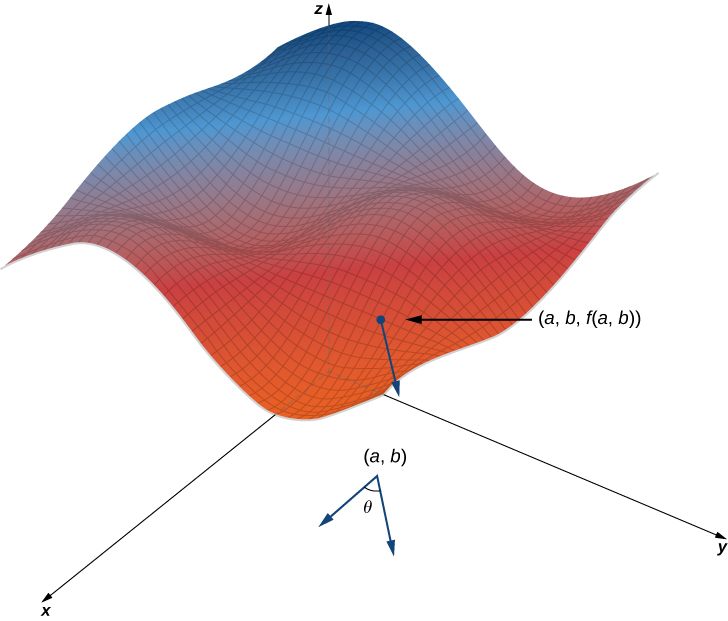
Figure 1. Finding the directional derivative at a point on the graph of [latex]z=f(x,y)[/latex]. The slope of the black arrow on the graph indicates the value of the directional derivative at that point.
We can calculate the slope of the secant line by dividing the difference in [latex]z[/latex]-values by the length of the line segment connecting the two points in the domain. The length of the line segment is [latex]h[/latex]. Therefore, the slope of the secant line is
[latex]\LARGE{m_{\text{sec}}=\frac{f(a+h\cos\theta,\,b+h\sin\theta)-f(a,\,b)}{h}}[/latex]
To find the slope of the tangent line in the same direction, we take the limit as [latex]h[/latex] approaches zero.
Definition
Suppose [latex]z=f(x, y)[/latex] is a function of two variables with a domain of [latex]D[/latex]. Let [latex](a,b)\in{D}[/latex] and define [latex]{\bf{u}}=(\cos\theta){\bf{i}}+(\sin\theta)\bf{j}[/latex]. Then the directional derivative of [latex]f[/latex] in the direction of [latex]\bf{u}[/latex] is given by
[latex]\large{D_{\bf{u}}f(a,b)=\displaystyle\lim_{h\to0}\frac{f(a+h\cos\theta,b+h\sin\theta)-f(a,b)}{h}},[/latex]
provided the limit exists.
The directional derivative of [latex]f[/latex] in the direction of [latex]\bf{u}[/latex] provides a formal definition of the directional derivative that can be used in many cases to calculate a directional derivative.
Example: finding the Directional derivative from the definition
Let [latex]\theta=\arccos(3/5)[/latex]. Find the directional derivative [latex]D_{\bf{u}}f(x,y)[/latex] of [latex]f(x,y)=x^2-xy+3y^2[/latex] in the direction of [latex]{\bf{u}}=(\cos\theta){\bf{i}}+(\sin\theta)\bf{j}[/latex]. What is [latex]D_{\bf{u}}f(-1,2)[/latex]?
Another approach to calculating a directional derivative involves partial derivatives, as outlined in the following theorem.
Theorem: Directional derivative of a function of two variables
Let [latex]z=f(x, y)[/latex] be a function of two variables [latex]x[/latex] and [latex]y[/latex], and assume that [latex]f_x[/latex] and [latex]f_y[/latex] exist. Then the directional derivative of [latex]f[/latex] in the direction of [latex]{\bf{u}}=\cos\theta{\bf{i}}+\sin\theta\bf{j}[/latex] is given by
[latex]\large{D_{\bf{u}}f(x,y)=f_x(x,y)\cos\theta+f_y(x,y)\sin\theta}.[/latex]
Proof
The directional derivative of [latex]f[/latex] in the direction of [latex]\bf{u}[/latex] states that the directional derivative of [latex]f[/latex] in the direction of [latex]{\bf{u}}=\cos\theta{\bf{i}}+\sin\theta\bf{j}[/latex] is given by
[latex]D_{\bf{u}}f(a,b)=\displaystyle\lim_{h\to0}\frac{f(a+h\cos\theta,b+h\sin\theta)-f(a,b)}{h}[/latex]
Let [latex]x=a+t\cos\theta[/latex] and [latex]y=b+t\sin\theta[/latex], and define [latex]g(t)=f(x, y)[/latex]. Since [latex]f_x[/latex] and [latex]f_y[/latex] both exist, and therefore [latex]f[/latex] is differentiable, we can use the chain rule for functions of two variables to calculate [latex]{g}'(t)[/latex]:
[latex]\hspace{8.5cm}\begin{align} g'(t)&=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt} \\ &=f_x(x,y)\cos\theta+f_y(x,y)\sin\theta. \end{align}[/latex]
If [latex]t=0[/latex], then [latex]x=x_0(=a)[/latex] and [latex]y=y_0(=b)[/latex], so
[latex]g'(0)=f_x(x_0,y_0)\cos\theta+f_y(x_0,y_0)\sin\theta[/latex]
By the definition of [latex]{g}'(t)[/latex], it is also true that
[latex]\hspace{8.5cm}\begin{align} g'(0)&=\displaystyle\lim_{t\to0}\frac{g(t)-g(0)}t \\ &=\displaystyle\lim_{t\to0}\frac{f(x_0+t\cos\theta,y_0+t\sin\theta)-f(x_0,y_0)}t. \end{align}[/latex]
Therefore, [latex]D_{\bf{u}}f(x_0,y_0)=f_x(x,y)\cos\theta+f_y(x,y)\sin\theta[/latex].
[latex]_\blacksquare[/latex]
Example: Finding a directional derivative: Alternative Method
Let [latex]\theta=\arccos(3/5)[/latex]. Find the directional derivative [latex]D_{\bf{u}}f(x,y)[/latex] of [latex]f(x,y)=x^2-xy+3y^2[/latex] in the direction of [latex]{\bf{u}}=(\cos\theta){\bf{i}}+(\sin\theta)\bf{j}[/latex]. What is [latex]D_{\bf{u}}f(-1,2)[/latex]?
Try it
Find the directional derivative [latex]D_{\bf{u}}f(x,y)[/latex] of [latex]f(x,y)=3x^2y-4xy^3+3y^2-4x[/latex] in the direction of [latex]{\bf{u}}=(\cos\frac{\pi}3){\bf{i}}+(\sin\frac{\pi}3)\bf{j}[/latex] using the Directional Derivative of a Function of Two Variables. What is [latex]D_{\bf{u}}f(3,4)[/latex]?
Watch the following video to see the worked solution to the above Try It
If the vector that is given for the direction of the derivative is not a unit vector, then it is only necessary to divide by the norm of the vector. For example, if we wished to find the directional derivative of the function in Example: Finding a Directional Derivative: Alternative Method in the direction of the vector [latex]\langle-5,12\rangle[/latex] we would first divide by its magnitude to get [latex]\bf{u}[/latex]. This gives us [latex]{\bf{u}}=\langle-(5/13),12/13\rangle[/latex]. Then
[latex]\hspace{8.5cm}\begin{align} D_{\bf{u}}f(x,y)&=\nabla{f}(x,y)\cdot\bf{u} \\ &=-\frac5{13}(2x-y)+\frac{12}{13}(-x+6y) \\ &=-\frac{22}{13}x+\frac{17}{13}y. \end{align}[/latex]
Candela Citations
- CP 4.28. Authored by: Ryan Melton. License: CC BY: Attribution
- Calculus Volume 3. Authored by: Gilbert Strang, Edwin (Jed) Herman. Provided by: OpenStax. Located at: https://openstax.org/books/calculus-volume-3/pages/1-introduction. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike. License Terms: Access for free at https://openstax.org/books/calculus-volume-3/pages/1-introduction

