Applying Stokes’ Theorem

Stokes’ theorem translates between the flux integral of surface [latex]S[/latex] to a line integral around the boundary of [latex]S[/latex]. Therefore, the theorem allows us to compute surface integrals or line integrals that would ordinarily be quite difficult by translating the line integral into a surface integral or vice versa. We now study some examples of each kind of translation.

Example: calculating a surface integral

Calculate surface integral [latex]\displaystyle\iint_S\text{curl }{\bf{F}}\cdot{d}{\bf{S}}[/latex], where [latex]S[/latex] is the surface, oriented outward, in Figure 1 and [latex]{\bf{F}}=\langle{z},2xy,x+y\rangle[/latex].

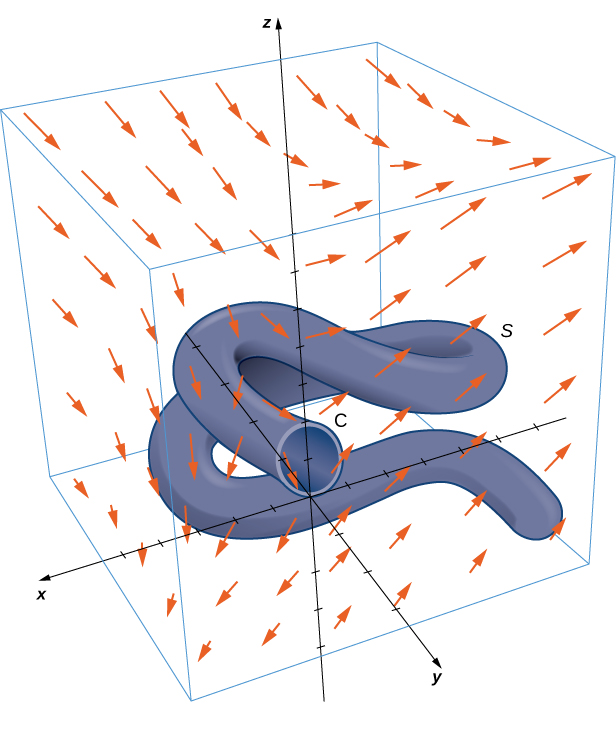
Figure 1. A complicated surface in a vector field.

Show Solution

Note that to calculate [latex]\displaystyle\iint_S\text{curl }{\bf{F}}\cdot{d}{\bf{S}}[/latex] without using Stokes’ theorem, we would need to use the equation to calculate scalar surface integrals. Use of this equation requires a parameterization of [latex]S[/latex]. Surface [latex]S[/latex] is complicated enough that it would be extremely difficult to find a parameterization. Therefore, the methods we have learned in previous sections are not useful for this problem. Instead, we use Stokes’ theorem, noting that the boundary [latex]C[/latex] of the surface is merely a single circle with radius 1.

The curl of [latex]{\bf{F}}[/latex] is [latex]\langle1,1,2y\rangle[/latex]. By Stokes’ theorem,

[latex]\large{\displaystyle\iint_S\text{curl }{\bf{F}}\cdot{d}{\bf{S}}=\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}}[/latex],

where [latex]C[/latex] has parameterization [latex]{\bf{r}}(t)=\langle\sin{t},0,1-\cos{t}\rangle[/latex], [latex]0\leq{t}\leq2\pi[/latex]. By the equation to for computing vector line integrals,

[latex]\begin{aligned} \displaystyle\iint_S\text{curl }{\bf{F}}\cdot{d}{\bf{S}}&=\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}} \\ &=\displaystyle\int_0^{2\pi}\langle1-\cos{t},0,-\sin{t}\rangle\cdot\langle-\cos{t},0\sin{t}\rangle{d}t \\ &=\displaystyle\int_0^{2\pi}(-\cos{t}+\cos^2t-\sin^2t)dt \\ &=\left[-\sin{t}+\frac12\sin(2t)\right]_0^{2\pi} \\ &=\left(-\sin{(2\pi)}+\frac12\sin{(4\pi)}\right)-\left(-\sin0+\frac12\sin0\right) \\ &=0 \end{aligned}[/latex].

An amazing consequence of Stokes’ theorem is that if [latex]S'[/latex] is any other smooth surface with boundary [latex]C[/latex] and the same orientation as [latex]S[/latex], then [latex]\displaystyle\iint_S\text{curl }{\bf{F}}\cdot{d}{\bf{S}}=\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}=0[/latex] because Stokes’ theorem says the surface integral depends on the line integral around the boundary only.

In Example “Calculating a Surface Integral”, we calculated a surface integral simply by using information about the boundary of the surface. In general, let [latex]S_1[/latex] and [latex]S_2[/latex] be smooth surfaces with the same boundary [latex]C[/latex] and the same orientation. By Stokes’ theorem,

[latex]\large{\displaystyle\iint_{S_1}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}=\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}=\displaystyle\iint_{S_2}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}}[/latex].

Therefore, if [latex]\displaystyle\iint_{S_1}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}[/latex] is difficult to calculate but [latex]\displaystyle\iint_{S_2}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}[/latex] is easy to calculate, Stokes’ theorem allows us to calculate the easier surface integral. In Example “Calculating a Surface Integral”, we could have calculated [latex]\displaystyle\iint_{S}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}[/latex] by calculating [latex]\displaystyle\iint_{S^\prime}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}[/latex], where [latex]S'[/latex] is the disk enclosed by boundary curve [latex]C[/latex] (a much more simple surface with which to work).

[latex]{\displaystyle\iint_{S_1}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}=\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}=\displaystyle\iint_{S_2}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}}[/latex] shows that flux integrals of curl vector fields are surface independent in the same way that line integrals of gradient fields are path independent. Recall that if [latex]{\bf{F}}[/latex] is a two-dimensional conservative vector field defined on a simply connected domain, [latex]f[/latex] is a potential function for [latex]{\bf{F}}[/latex], and [latex]C[/latex] is a curve in the domain of [latex]{\bf{F}}[/latex], then [latex]\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}[/latex] depends only on the endpoints of [latex]C[/latex]. Therefore if [latex]C'[/latex] is any other curve with the same starting point and endpoint as [latex]C[/latex] (that is, [latex]C'[/latex] has the same orientation as [latex]C[/latex]), then [latex]\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}=\displaystyle\int_{C^\prime}{\bf{F}}\cdot{d}{\bf{r}}[/latex]. In other words, the value of the integral depends on the boundary of the path only; it does not really depend on the path itself.

Analogously, suppose that [latex]S[/latex] and [latex]S'[/latex] are surfaces with the same boundary and same orientation, and suppose that [latex]{\bf{G}}[/latex] is a three-dimensional vector field that can be written as the curl of another vector field [latex]{\bf{F}}[/latex] (so that [latex]{\bf{F}}[/latex] is like a “potential field” of [latex]{\bf{G}}[/latex]). By [latex]{\displaystyle\iint_{S_1}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}=\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}=\displaystyle\iint_{S_2}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}}[/latex],

[latex]\large{\displaystyle\int_S{\bf{G}}\cdot{d}{\bf{S}}=\displaystyle\iint_{S}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}=\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}=\displaystyle\iint_{S^\prime}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}=\displaystyle\iint_{S^\prime}\text{curl }{\bf{G}}\cdot{d}{\bf{S}}}[/latex].

Therefore, the flux integral of [latex]{\bf{G}}[/latex] does not depend on the surface, only on the boundary of the surface. Flux integrals of vector fields that can be written as the curl of a vector field are surface independent in the same way that line integrals of vector fields that can be written as the gradient of a scalar function are path independent.

try it

Use Stokes’ theorem to calculate surface integral [latex]\displaystyle\iint_{S}\text{curl }{\bf{F}}\cdot{d}{\bf{S}}[/latex], where [latex]{\bf{F}}=\langle{z},x,y\rangle[/latex] and [latex]S[/latex] is the surface as shown in the following figure. The boundary curve, [latex]C[/latex], is oriented clockwise when looking along the positive [latex]y[/latex]-axis.

Show Solution

[latex]-\pi[/latex].

Example: calculating a line integral

Calculate the line integral [latex]\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}[/latex], where [latex]{\bf{F}}=\langle{x}y,x^2+y^2+z^2,yz\rangle[/latex] and [latex]C[/latex] is the boundary of the parallelogram with vertices [latex](0, 0, 1)[/latex], [latex](0, 1, 0)[/latex], [latex](2, 0, -1)[/latex], and [latex](2, 1, -2)[/latex].

Show Solution

To calculate the line integral directly, we need to parameterize each side of the parallelogram separately, calculate four separate line integrals, and add the result. This is not overly complicated, but it is time-consuming.

By contrast, let’s calculate the line integral using Stokes’ theorem. Let [latex]S[/latex] denote the surface of the parallelogram. Note that [latex]S[/latex] is the portion of the graph of [latex]z=1-x-y[/latex] for [latex](x, y)[/latex] varying over the rectangular region with vertices [latex](0, 0)[/latex], [latex](0, 1)[/latex], [latex](2, 0)[/latex], and [latex](2, 1)[/latex] in the [latex]xy[/latex]-plane. Therefore, a parameterization of [latex]S[/latex] is [latex]\langle{x},y,1-x-y\rangle[/latex], [latex]0\leq{x}\leq2, \ 0\leq{y}\leq1[/latex]. The curl of [latex]{\bf{F}}[/latex] is [latex]-\langle{z},0,x\rangle[/latex], and Stokes’ theorem and the equation to calculate scalar surface integrals give

[latex]\begin{aligned} \displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}&=\displaystyle\iint_S\text{curl }{\bf{F}}\cdot{d}{\bf{S}} \\ &=\displaystyle\int_0^2\displaystyle\int_0^1\text{curl }{\bf{F}}(x,y)\cdot({\bf{t}}_x\times{\bf{t}}_y)dydx \\ &=\displaystyle\int_0^2\displaystyle\int_0^1\langle-(1-x-y),0,x\rangle\cdot(\langle1,0,-1\rangle\times\langle0,1,-1\rangle)dydx \\ &=\displaystyle\int_0^2\displaystyle\int_0^1\langle{x}+y-1,0,x\rangle\cdot\langle1,1,1\rangle{d}ydx \\ &=\displaystyle\int_0^2\displaystyle\int_0^12x+y-1dydx \\ &=3 \end{aligned}[/latex].

try it

Use Stokes’ theorem to calculate line integral [latex]\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}[/latex], where [latex]{\bf{F}}=\langle{z},x,y\rangle[/latex] and [latex]C[/latex] is oriented clockwise and is the boundary of a triangle with vertices [latex](0, 0, 1)[/latex], [latex](3, 0, -2)[/latex], and [latex](0, 1, 2)[/latex].

Show Solution

[latex]\frac32[/latex].

Watch the following video to see the worked solution to the above Try It

You can view the transcript for “CP 6.63” here (opens in new window).

Interpretation of Curl

In addition to translating between line integrals and flux integrals, Stokes’ theorem can be used to justify the physical interpretation of curl that we have learned. Here we investigate the relationship between curl and circulation, and we use Stokes’ theorem to state Faraday’s law—an important law in electricity and magnetism that relates the curl of an electric field to the rate of change of a magnetic field.

Recall that if [latex]C[/latex] is a closed curve and [latex]{\bf{F}}[/latex] is a vector field defined on [latex]C[/latex], then the circulation of [latex]{\bf{F}}[/latex] around [latex]C[/latex] is line integral [latex]\displaystyle\int_C{\bf{F}}\cdot{d}{\bf{r}}[/latex]. If [latex]{\bf{F}}[/latex] represents the velocity field of a fluid in space, then the circulation measures the tendency of the fluid to move in the direction of [latex]C[/latex].

Let [latex]{\bf{F}}[/latex] be a continuous vector field and let [latex]D_r[/latex] be a small disk of radius [latex]r[/latex] with center [latex]P_0[/latex] (Figure 2). If [latex]D_r[/latex] is small enough, then [latex](\text{curl }{\bf{F}})(P)\approx(\text{curl }{\bf{F}})(P_0)[/latex] for all points [latex]P[/latex] in [latex]D_r[/latex] because the curl is continuous. Let [latex]C_r[/latex] be the boundary circle of [latex]D_r[/latex]. By Stokes’ theorem,

[latex]\large{\displaystyle\int_{C_r}{\bf{F}}\cdot{d}{\bf{r}}=\displaystyle\iint_{D_r}\text{curl }{\bf{F}}\cdot{\bf{N}}{d}S\approx\displaystyle\iint_{D_r}(\text{curl }{\bf{F}})(P_0)\cdot{\bf{N}}(P_0)dS}[/latex].

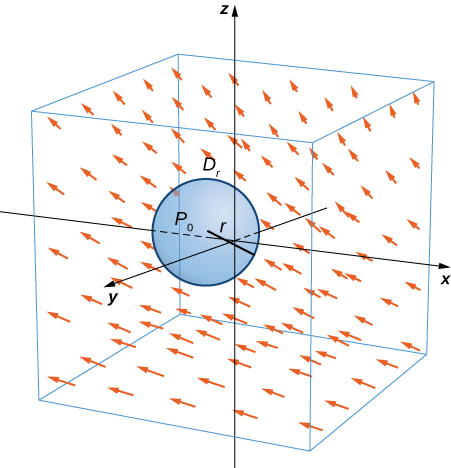
Figure 2. Disk [latex]{D_r}[/latex] is a small disk in a continuous vector field.

The quantity [latex](\text{curl }{\bf{F}})(P_0)\cdot{\bf{N}}(P_0)[/latex] is constant, and therefore

[latex]\large{\displaystyle\iint_{D_r}(\text{curl }{\bf{F}})(P_0)\cdot{\bf{N}}(P_0)dS=\pi{r}^2[(\text{curl }{\bf{F}})(P_0)\cdot{\bf{N}}(P_0)]}[/latex].

Thus

[latex]\large{\displaystyle\int_{C_r}{\bf{F}}\cdot{d}{\bf{r}}\approx\pi{r}^2[(\text{curl }{\bf{F}})(P_0)\cdot{\bf{N}}(P_0)]}[/latex],

and the approximation gets arbitrarily close as the radius shrinks to zero. Therefore Stokes’ theorem implies that

[latex]\large{(\text{curl }{\bf{F}})(P_0)\cdot{\bf{N}}(P_0)=\displaystyle\lim_{r\to0^+}\frac{1}{\pi{r^2}}\displaystyle\int_{C_r}{\bf{F}}\cdot{d}{\bf{r}}}[/latex].

This equation relates the curl of a vector field to the circulation. Since the area of the disk is [latex]\pi{r}^2[/latex], this equation says we can view the curl (in the limit) as the circulation per unit area. Recall that if [latex]{\bf{F}}[/latex] is the velocity field of a fluid, then circulation [latex]\displaystyle\oint_{c_r}{\bf{F}}\cdot{d}{\bf{r}}=\displaystyle\oint_{C_r}{\bf{F}}\cdot{\bf{T}}ds[/latex] is a measure of the tendency of the fluid to move around [latex]C_r[/latex]. The reason for this is that [latex]{\bf{F}}\cdot{\bf{T}}[/latex] is a component of [latex]{\bf{F}}[/latex] in the direction of [latex]{\bf{T}}[/latex], and the closer the direction of [latex]{\bf{F}}[/latex] is to [latex]{\bf{T}}[/latex], the larger the value of [latex]{\bf{F}}\cdot{\bf{T}}[/latex] (remember that if [latex]{\bf{a}}[/latex] and [latex]{\bf{b}}[/latex] are vectors and [latex]{\bf{b}}[/latex] is fixed, then the dot product [latex]{\bf{a}}\cdot{\bf{b}}[/latex] is maximal when [latex]{\bf{a}}[/latex] points in the same direction as [latex]{\bf{b}}[/latex]). Therefore, if [latex]{\bf{F}}[/latex] is the velocity field of a fluid, then [latex]\text{curl }{\bf{F}}\cdot{\bf{N}}[/latex] is a measure of how the fluid rotates about axis [latex]{\bf{N}}[/latex]. The effect of the curl is largest about the axis that points in the direction of [latex]{\bf{N}}[/latex], because in this case [latex]{\bf{F}}\cdot{\bf{N}}[/latex] is as large as possible.

To see this effect in a more concrete fashion, imagine placing a tiny paddlewheel at point [latex]P_0[/latex] (Figure 3). The paddlewheel achieves its maximum speed when the axis of the wheel points in the direction of [latex]\text{curl }{\bf{F}}[/latex]. This justifies the interpretation of the curl we have learned: curl is a measure of the rotation in the vector field about the axis that points in the direction of the normal vector [latex]{\bf{N}}[/latex], and Stokes’ theorem justifies this interpretation.

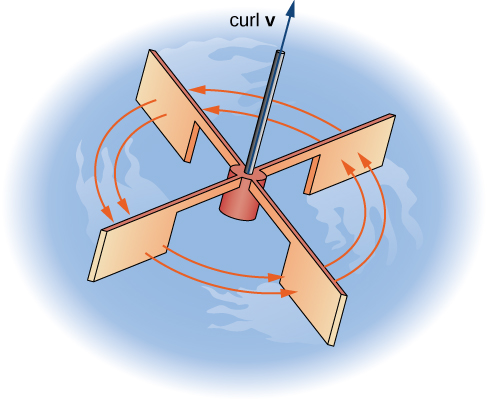
Figure 3. To visualize curl at a point, imagine placing a tiny paddlewheel at that point in the vector field.

Now that we have learned about Stokes’ theorem, we can discuss applications in the area of electromagnetism. In particular, we examine how we can use Stokes’ theorem to translate between two equivalent forms of Faraday’s law. Before stating the two forms of Faraday’s law, we need some background terminology.

Let [latex]C[/latex] be a closed curve that models a thin wire. In the context of electric fields, the wire may be moving over time, so we write [latex]C(t)[/latex] to represent the wire. At a given time [latex]t[/latex], curve [latex]C(t)[/latex] may be different from original curve [latex]C[/latex] because of the movement of the wire, but we assume that [latex]C(t)[/latex] is a closed curve for all times [latex]t[/latex]. Let [latex]D(t)[/latex] be a surface with [latex]C(t)[/latex] as its boundary, and orient [latex]C(t)[/latex] so that [latex]D(t)[/latex] has positive orientation. Suppose that [latex]C(t)[/latex] is in a magnetic field [latex]{\bf{B}}(t)[/latex] that can also change over time. In other words, [latex]{\bf{b}}[/latex] has the form

[latex]\large{{\bf{B}}(x,y,z)=\langle{P}(x,y,z),Q(x,y,z),R(x,y,z)\rangle}[/latex],

where [latex]P[/latex], [latex]Q[/latex], and [latex]R[/latex] can all vary continuously over time. We can produce current along the wire by changing field [latex]{\bf{B}}(t)[/latex] (this is a consequence of Ampere’s law). Flux [latex]\phi(t)=\displaystyle\iint_{D(t)}{\bf{B}}(t)\cdot{d}{\bf{S}}[/latex] creates electric field [latex]{\bf{E}}(t)[/latex] that does work. The integral form of Faraday’s law states that

[latex]\large{\text{Work }=\displaystyle\int_{C(t)}{\bf{E}}(t)\cdot{d}{\bf{r}}=-\frac{\partial\phi}{\partial{t}}}[/latex].

In other words, the work done by [latex]{\bf{E}}[/latex] is the line integral around the boundary, which is also equal to the rate of change of the flux with respect to time. The differential form of Faraday’s law states that

[latex]\large{\text{curl }{\bf{E}}=-\frac{\partial{\bf{B}}}{\partial{t}}}[/latex].

Using Stokes’ theorem, we can show that the differential form of Faraday’s law is a consequence of the integral form. By Stokes’ theorem, we can convert the line integral in the integral form into surface integral

[latex]\large{-\frac{\partial\phi}{\partial{t}}=\displaystyle\int_{C(t)}{\bf{E}}(t)\cdot{d}{\bf{r}}=\displaystyle\iint_{D(t)}\text{curl }{\bf{E}}(t)\cdot{d}{\bf{S}}}[/latex].

Since [latex]\phi(t)=\displaystyle\iint_{D(t)}{\bf{B}}(t)\cdot{d}{\bf{S}}[/latex], then as long as the integration of the surface does not vary with time we also have

[latex]\large{-\frac{\partial\phi}{\partial{t}}=\displaystyle\iint_{D(t)}-\frac{\partial{\bf{B}}}{\partial{t}}\cdot{d}{\bf{S}}}[/latex].

Therefore,

[latex]\large{\displaystyle\iint_{D(t)}-\frac{\partial{\bf{B}}}{\partial{t}}\cdot{d}{\bf{S}}=\displaystyle\iint_{D(t)}\text{curl }{\bf{E}}(t)\cdot{d}{\bf{S}}}[/latex].

To derive the differential form of Faraday’s law, we would like to conclude that [latex]\text{curl }{\bf{E}}=-\frac{\partial{\bf{B}}}{\partial{t}}[/latex]. In general, the equation

[latex]large{\displaystyle\iint_{D(t)}-\frac{\partial{\bf{B}}}{\partial{t}}\cdot{d}{\bf{S}}=\displaystyle\iint_{D(t)}\text{curl }{\bf{E}}(t)\cdot{d}{\bf{S}}}[/latex]

is not enough to conclude that [latex]\text{curl }{\bf{E}}=-\frac{\partial{\bf{B}}}{\partial{t}}[/latex]. The integral symbols do not simply “cancel out,” leaving equality of the integrands. To see why the integral symbol does not just cancel out in general, consider the two single-variable integrals [latex]\displaystyle\int_0^1xdx[/latex] and [latex]\displaystyle\int_0^1f(x)dx[/latex], where

[latex]f(x)=\begin{array}{cc} \{ & \begin{array}{cc} 1, & 0\leq{x}\leq1/2 \\ 0,& 1/2\leq{x}\leq1 \end{array} \end{array}[/latex].

Both of these integrals equal [latex]\frac12[/latex],  so[latex]\displaystyle\int_0^1xdx=\displaystyle\int_0^1f(x)dx[/latex]. However, [latex]x\ne{f}(x)[/latex]. Analogously, with our equation [latex]\displaystyle\iint_{D(t)}-\frac{\partial{\bf{B}}}{\partial{t}}\cdot{d}{\bf{S}}=\displaystyle\iint_{D(t)}\text{curl }{\bf{E}}(t)\cdot{d}{\bf{S}}[/latex], we cannot simply conclude that [latex]\text{curl }{\bf{E}}=-\frac{\partial{\bf{B}}}{\partial{t}}[/latex] just because their integrals are equal. However, in our context, equation [latex]\displaystyle\iint_{D(t)}-\frac{\partial{\bf{B}}}{\partial{t}}\cdot{d}{\bf{S}}=\displaystyle\iint_{D(t)}\text{curl }{\bf{E}}(t)\cdot{d}{\bf{S}}[/latex] is true for any region, however small (this is in contrast to the single-variable integrals just discussed). If [latex]{\bf{F}}[/latex] and [latex]{\bf{G}}[/latex] are three-dimensional vector fields such that [latex]\displaystyle\iint_S{\bf{F}}\cdot{d}{\bf{S}}=\displaystyle\iint_S{\bf{G}}\cdot{d}{\bf{S}}[/latex] for any surface [latex]S[/latex], then it is possible to show that [latex]{\bf{F}}={\bf{G}}[/latex] by shrinking the area of [latex]S[/latex] to zero by taking a limit (the smaller the area of [latex]S[/latex], the closer the value of [latex]\displaystyle\iint_S{\bf{F}}\cdot{d}{\bf{S}}[/latex] to the value of [latex]{\bf{F}}[/latex] at a point inside [latex]S[/latex]). Therefore, we can let area [latex]D(t)[/latex] shrink to zero by taking a limit and obtain the differential form of Faraday’s law:

[latex]\large{\text{curl }{\bf{E}}=-\frac{\partial{\bf{B}}}{\partial{t}}}[/latex].

In the context of electric fields, the curl of the electric field can be interpreted as the negative of the rate of change of the corresponding magnetic field with respect to time.

Watch the following video to see the worked solution to the above Try It