Learning Objectives
- Recognize the main features of ellipsoids, paraboloids, and hyperboloids.
- Use traces to draw the intersections of quadric surfaces with the coordinate planes.
Quadric Surfaces
We have learned about surfaces in three dimensions described by first-order equations; these are planes. Some other common types of surfaces can be described by second-order equations. We can view these surfaces as three-dimensional extensions of the conic sections we discussed earlier: the ellipse, the parabola, and the hyperbola. We call these graphs quadric surfaces.
DEFINITION
Quadric surfaces are the graphs of equations that can be expressed in the form
[latex]Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0[/latex].
When a quadric surface intersects a coordinate plane, the trace is a conic section. Since these conic sections show up frequently in this section, we review some commonly encountered equations briefly below:
Recall: Equations of Conic Sections
The equation [latex]x^2 = 4py[/latex], where [latex]p[/latex] is a constant, represents a parabola; the parabola is opening upward if [latex]p>0[/latex] and downward if [latex]p<0[/latex]. Similarly, the equation [latex]y^2 = 4px[/latex], where [latex]p[/latex] is a constant, also represents a parabola; the parabola is opening rightward if [latex]p>0[/latex] and leftward if [latex]p<0[/latex]. The equation [latex]\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1[/latex], where [latex]a \text{ and } b[/latex] are constants, represents an ellipse. It has a horizontal major axis if [latex]a > b > 0[/latex] and a vertical major axis if [latex]b > a > 0[/latex]. The length of its horizontal axis is [latex]2a[/latex] and the length of its vertical axis is [latex]2b[/latex].
The equation [latex]\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1[/latex], OR the equation [latex]\frac{y^2}{b^2} - \frac{x^2}{a^2} = 1[/latex] where [latex]a \text{ and } b[/latex] are constants, represents an hyperbola. The hyperbola has two branches opening either to the right and left, in the case of the first equation, or up and down, in the case of the second equation.
An ellipsoid is a surface described by an equation of the form [latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1[/latex]. Set [latex]x=0[/latex] to see the trace of the ellipsoid in the [latex]yz[/latex]-plane. To see the traces in the [latex]xy[/latex]– and [latex]xz[/latex]-planes, set [latex]z=0[/latex] and [latex]y=0[/latex], respectively. Notice that, if [latex]a=b[/latex], the trace in the [latex]xy[/latex]-plane is a circle. Similarly, if [latex]a=c[/latex], the trace in the [latex]xz[/latex]-plane is a circle and, if [latex]b=c[/latex] then the trace in the [latex]yz[/latex]-plane is a circle. A sphere, then, is an ellipsoid with [latex]a=b=c[/latex].
Example: sketching an ellipsoid
Sketch the ellipsoid [latex]\frac{x^2}{2^2}+\frac{y^2}{3^2}+\frac{z^2}{5^2}=1[/latex].
The trace of an ellipsoid is an ellipse in each of the coordinate planes. However, this does not have to be the case for all quadric surfaces. Many quadric surfaces have traces that are different kinds of conic sections, and this is usually indicated by the name of the surface. For example, if a surface can be described by an equation of the form [latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{z}{c}[/latex], then we call that surface an elliptic paraboloid. The trace in the [latex]xy[/latex]-plane is an ellipse, but the traces in the [latex]xz[/latex]-plane and [latex]yz[/latex]-plane are parabolas (Figure 3). Other elliptic paraboloids can have other orientations simply by interchanging the variables to give us a different variable in the linear term of the equation [latex]\frac{x^2}{a^2}+\frac{z^2}{c^2}=\frac{y}{b}[/latex] or [latex]\frac{y^2}{b^2}+\frac{z^2}{c^2}=\frac{x}{a}[/latex].

Figure 3. This quadric surface is called an elliptic paraboloid.
Example: identifying traces of quadric surfaces
Describe the traces of the elliptic paraboloid [latex]x^2+\frac{y^2}{2^2}=\frac{z}{5}[/latex].
try it
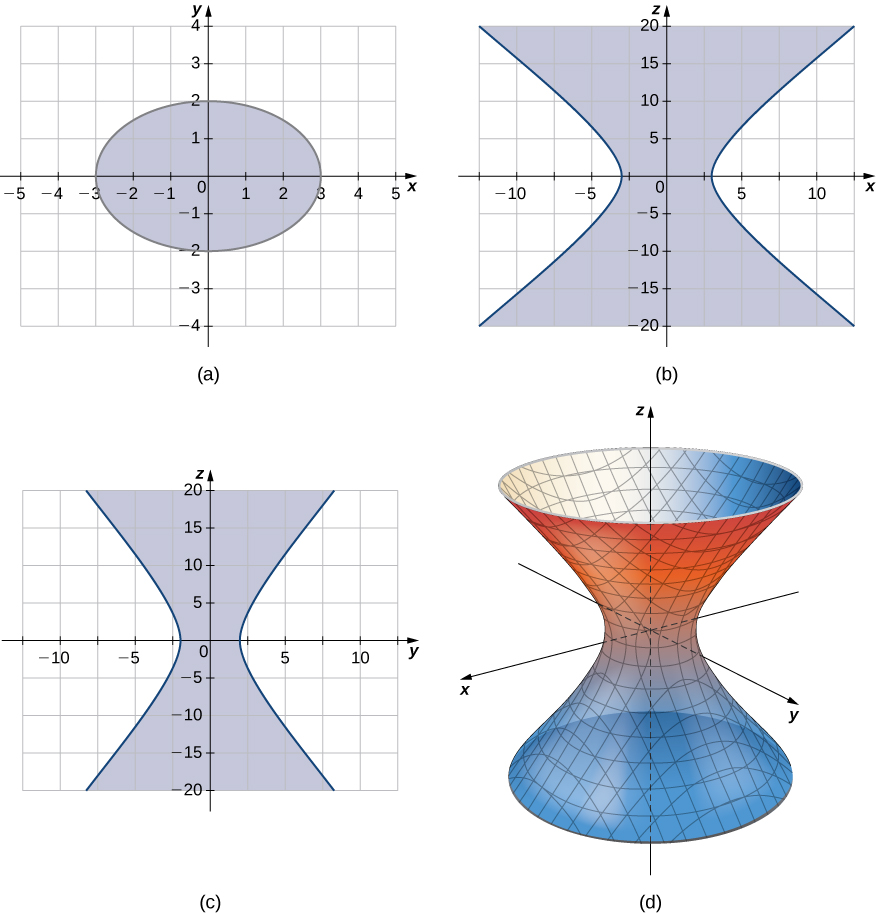
A hyperboloid of one sheet is any surface that can be described with an equation of the form [latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1[/latex]. Describe the traces of the hyperboloid of one sheet given by equation [latex]\frac{x^2}{3^2}+\frac{y^2}{2^2}-\frac{z^2}{5^2}=1[/latex].
Watch the following video to see the worked solution to the above Try IT.
Hyperboloids of one sheet have some fascinating properties. For example, they can be constructed using straight lines, such as in the sculpture in Figure 6(a). In fact, cooling towers for nuclear power plants are often constructed in the shape of a hyperboloid. The builders are able to use straight steel beams in the construction, which makes the towers very strong while using relatively little material (Figure 6(b)).

Figure 6. (a) A sculpture in the shape of a hyperboloid can be constructed of straight lines. (b) Cooling towers for nuclear power plants are often built in the shape of a hyperboloid.
Example: chapter opener: Finding the focus of a parabolic reflector
Energy hitting the surface of a parabolic reflector is concentrated at the focal point of the reflector (Figure 7). If the surface of a parabolic reflector is described by equation [latex]\frac{x^2}{100}+\frac{y^2}{100}=\frac{z}{4}[/latex], where is the focal point of the reflector?

Figure 7. Energy reflects off of the parabolic reflector and is collected at the focal point. (credit: modification of CGP Grey, Wikimedia Commons)
Seventeen standard quadric surfaces can be derived from the general equation
[latex]Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0[/latex].
The following figures summarizes the most important ones.

Figure 8. Characteristics of Common Quadratic Surfaces: Ellipsoid, Hyperboloid of One Sheet, Hyperboloid of Two Sheets.

Figure 9. Characteristics of Common Quadratic Surfaces: Elliptic Cone, Elliptic Paraboloid, Hyperbolic Paraboloid.
Example: identifying equations of quadric surfaces
Identify the surfaces represented by the given equations.
- [latex]16x^{2}+9y^{2}+16z^{2}=144[/latex]
- [latex]9x^{2}-18x+4y^{2}+16y-36z+25=0[/latex]
try it
Identify the surface represented by equation [latex]9x^{2}+y^{2}-z^{2}+2z-10=0[/latex].
Candela Citations
- CP 2.53. Authored by: Ryan Melton. License: CC BY: Attribution
- Calculus Volume 3. Authored by: Gilbert Strang, Edwin (Jed) Herman. Provided by: OpenStax. Located at: https://openstax.org/books/calculus-volume-3/pages/1-introduction. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike. License Terms: Access for free at https://openstax.org/books/calculus-volume-3/pages/1-introduction