Learning Objectives
- Determine the gradient vector of a given real-valued function.
- Explain the significance of the gradient vector with regard to direction of change along a surface.
- Use the gradient to find the tangent to a level curve of a given function.
The right-hand side of the Directional Derivative of a Function of Two Variables is equal to [latex]f_x(x,y)\cos\theta+f_y(x,y)\sin\theta[/latex], which can be written as the dot product of two vectors. Define the first vector as [latex]\nabla{f}(x,y)=f_x(x,y){\bf{i}}+f_y(x,y)\bf{j}[/latex] and the second vector as [latex]{\bf{u}}=(\cos\theta){\bf{i}}+(\sin\theta)\bf{j}[/latex]. Then the right-hand side of the equation can be written as the dot product of these two vectors:
[latex]D_{\bf{u}}f(x,y)=\nabla{f}(x,y)\cdot\bf{u}.[/latex]
The first vector in the previous equation has a special name: the gradient of the function [latex]f[/latex]. The symbol [latex]\nabla[/latex] is called nabla and the vector [latex]\nabla{f}[/latex] is read “del [latex]f[/latex]“.
Definition
Let [latex]z=f(x, y)[/latex] be a function of [latex]x[/latex] and [latex]x[/latex] such that [latex]f_x[/latex] and [latex]f_y[/latex] exist. The vector [latex]\nabla{f}(x,y)[/latex] is called the gradient of [latex]f[/latex] and is defined as
[latex]\nabla{f}(x,y)=f_x(x,y){\bf{i}}+f_y(x,y){\bf{j}}.[/latex]
The vector [latex]\nabla{f}(x,y)[/latex] is also written as “grad [latex]f[/latex]“.
Example: finding gradients
Find the gradient [latex]\nabla{f}(x,y)[/latex] of each of the following functions:
a. [latex]f(x,y)=x^2-xy+3y^2[/latex]
b. [latex]f(x,y)=\sin{3x}\cos{3y}[/latex]
Try it
Find the gradient [latex]\nabla{f}(x,y)[/latex] of [latex]f(x,y)=(x^2-3y^2)/(2x+y)[/latex].
Try It
The gradient has some important properties. We have already seen one formula that uses the gradient: the formula for the directional derivative. Recall from The Dot Product that if the angle between two vectors [latex]\bf{a}[/latex] and [latex]\bf{b}[/latex] is [latex]\varphi[/latex], then [latex]{\bf{a}}\cdot{\bf{b}}=\|{\bf{a}}\|\|{\bf{b}}\|\cos\varphi[/latex]. Therefore, if the angle between [latex]\nabla{f}(x_0,y_0)[/latex] and [latex]{\bf{u}}=(\cos\theta){\bf{i}}+(\sin\theta){\bf{j}}[/latex] is [latex]\varphi[/latex], we have
[latex]\large{D_{\bf{u}}f(x_0,y_0)=\nabla{f}(x_0,y_0)\cdot{\bf{u}}=\|\nabla{f}(x_0,y_0)\|\|{\bf{u}}\|\cos\varphi=\|\nabla{f}(x_0,y_0)\|\cos\varphi}[/latex]
The [latex]\|{\bf{u}}\|[/latex] disappears because [latex]\bf{u}[/latex] is a unit vector. Therefore, the directional derivative is equal to the magnitude of the gradient evaluated at [latex](x_0, y_0)[/latex], multiplied by [latex]\cos\varphi[/latex]. Recall that [latex]\cos\varphi[/latex] ranges from [latex]-1[/latex] to [latex]1[/latex]. If [latex]\varphi=0[/latex], then [latex]\cos\varphi=1[/latex] and [latex]\nabla{f}(x_0,y_0)[/latex] and [latex]\bf{u}[/latex] point in opposite directions. In the first case, the value of [latex]D_{\bf{u}}f(x_0,y_0)[/latex] is maximized; in the second case, the value of [latex]D_{\bf{u}}f(x_0,y_0)[/latex] is minimized. If [latex]\nabla{f}(x_0,y_0)=0[/latex], then [latex]D_{\bf{u}}f(x_0,y_0)=\nabla{f}(x_0,y_0)\cdot{\bf{u}}=0[/latex] for any vector [latex]\bf{u}[/latex]. These cases are outlined in the following theorem.
Theorem: properties of the gradient
Suppose the function [latex]z=f(x, y)[/latex] is differentiable at [latex](x_0, y_0)[/latex] (Figure 3).
i. If [latex]\nabla{f}(x_0,y_0)=0[/latex], then [latex]D_{\bf{u}}f(x_0,y_0)=0[/latex] for any unit vector [latex]\bf{u}[/latex].
ii. If [latex]\nabla{f}(x_0,y_0)\ne 0[/latex], then [latex]D_{\bf{u}}f(x_0,y_0)[/latex] is maximized when [latex]\bf{u}[/latex] points in the same direction as [latex]\nabla{f}(x_0,y_0)[/latex]. The maximum value of [latex]D_{\bf{u}}f(x_0,y_0)[/latex] is [latex]\|\nabla{f}(x_0,y_0)\|[/latex].
iii. If [latex]\nabla{f}(x_0,y_0)\ne 0[/latex], then [latex]D_{\bf{u}}f(x_0,y_0)[/latex] is minimized when [latex]\bf{u}[/latex] points in the opposite direction from [latex]\nabla{f}(x_0,y_0)[/latex]. The minimum value of [latex]D_{\bf{u}}f(x_0,y_0)[/latex] is [latex]-\|\nabla{f}(x_0,y_0)\|[/latex].
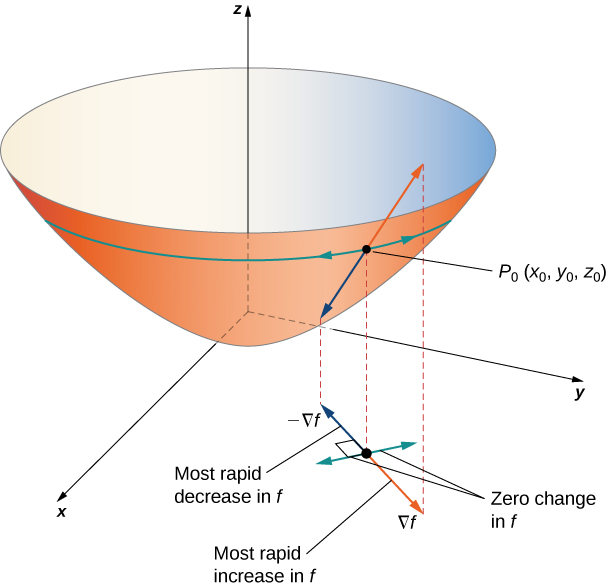
Figure 1. The gradient indicates the maximum and minimum values of the directional derivative at a point.
Example: finding a maximum directional derivative
Find the direction for which the directional derivative of [latex]f(x, y)=3x^{2}-4xy+2y^{2}[/latex] at [latex](-2, 3)[/latex] is a maximum. What is the maximum value?
Try it
Find the direction for which the directional derivative of [latex]g(x, y)=4x-xy+2y^{2}[/latex] at [latex](-2, 3)[/latex] is a maximum. What is the maximum value?
Watch the following video to see the worked solution to the above Try It
.
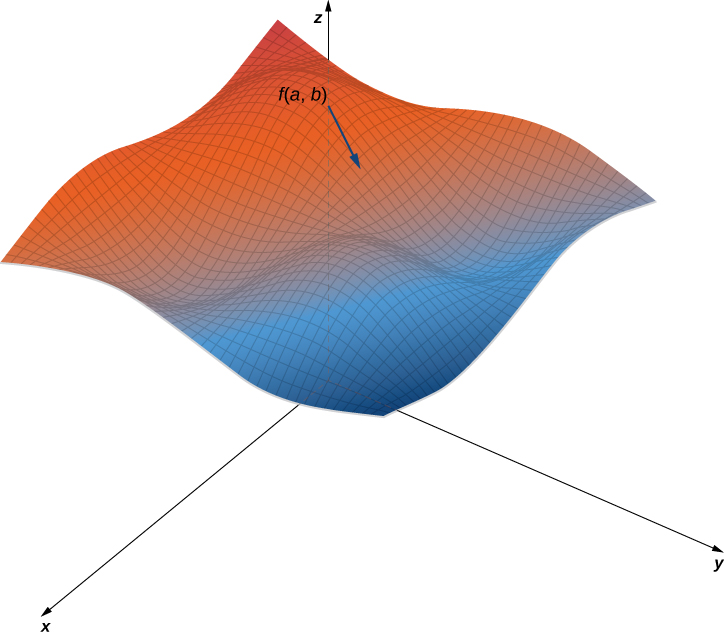
Figure 3. A typical surface in [latex]\mathbb{R}^{3}[/latex]. Given a point on the surface, the directional derivative can be calculated using the gradient.
When using a topographical map, the steepest slope is always in the direction where the contour lines are closest together (see Figure 6). This is analogous to the contour map of a function, assuming the level curves are obtained for equally spaced values throughout the range of that function.
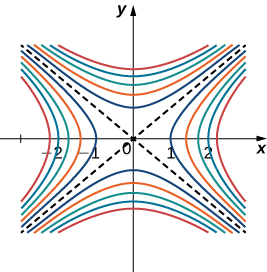
Figure 4. Contour map for the function [latex]\small{f(x,y)=x^{2}-y^{2}}[/latex] using level values between [latex]\small{-5}[/latex] and [latex]\small{5}[/latex].
Gradients and Level Curves
Recall that if a curve is defined parametrically by the function pair [latex](x(t), y(t))[/latex], then the vector [latex]x'(t){\bf{i}}+y'(t){\bf{j}}[/latex] is tangent to the curve for every value of [latex]t[/latex] in the domain. Now let’s assume [latex]z=f(x, y)[/latex] is a differentiable function of [latex]x[/latex] and [latex]y[/latex], and [latex](x_0, y_0)[/latex] is in its domain. Let’s suppose further that [latex]x_0=x(t_0)[/latex] and [latex]y_0=y(t_0)[/latex] for some value of [latex]t[/latex], and consider the level curve [latex]f(x, y)=k[/latex]. Define [latex]g(t)=f(x(t), y(t))[/latex] and calculate [latex]{g}'(t)[/latex] on the level curve. By the Chain Rule,
[latex]\large{g'(t)=f_x(x(t),y(t))x'(t)+f_y(x(t),y(t))y'(t)}.[/latex]
But [latex]g'(t)=0[/latex] because [latex]g(t)=k[/latex] for all [latex]t[/latex]. Therefore, on the one hand,
[latex]\large{f_x(x(t),y(t))x'(t)+f_y(x(t),y(t))y'(t)=0};[/latex]
on the other hand,
[latex]\large{f_x(x(t),y(t))x'(t)+f_y(x(t),y(t))y'(t)=\nabla{f}(x,y)\cdot\langle{x}'(t),y'(t)\rangle}.[/latex]
Therefore,
[latex]\large{\nabla{f}(x,y)\cdot\langle{x}'(t),y'(t)\rangle=0}.[/latex]
Thus, the dot product of these vectors is equal to zero, which implies they are orthogonal. However, the second vector is tangent to the level curve, which implies the gradient must be normal to the level curve, which gives rise to the following theorem.
Theorem: Gradient is normal to the level curve
Suppose the function [latex]z=f(x, y)[/latex] has continuous first-order partial derivatives in an open disk centered at a point [latex](x_0, y_0)[/latex]. If [latex]\nabla{f}(x_0,y_0)\ne0[/latex], then [latex]\nabla{f}(x_0,y_0)[/latex] is normal to the level curve of [latex]f[/latex] at [latex](x_0, y_0)[/latex].
We can use this theorem to find tangent and normal vectors to level curves of a function.
Example: Finding Tangents to level curves
For the function [latex]f(x, y)=2x^{2}-3xy+8y^{2}+2x-4y+4[/latex], find a tangent vector to the level curve at point [latex](-2, 1)[/latex]. Graph the level curve corresponding to [latex]f(x, y)=18[/latex] and draw in [latex]\nabla{f}(-2,1)[/latex] and a tangent vector.
Try it
For the function [latex]f(x,y)=x^2-2xy+5y^2+3x-2y+4[/latex], find the tangent to the level curve at point [latex](1, 1)[/latex]. Draw the graph of the level curve corresponding to [latex]f(x, y)=8[/latex] and draw [latex]\nabla{f}(1,1)[/latex] and a tangent vector.
