Learning Objectives
- Use double integrals in polar coordinates to calculate areas and volumes.
As in rectangular coordinates, if a solid [latex]S[/latex] is bounded by the surface [latex]{z} = {f}{(r,{\theta})}[/latex], as well as by the surfaces [latex]{r} = {a}, {r} = {b}, {\theta} = {\alpha}[/latex], and [latex]{\theta} = {\beta}[/latex] we can find the volume [latex]V[/latex] of [latex]S[/latex] by double integration, as
[latex]\large{{V} = \underset{R}{\displaystyle\iint}{f}{(r,{\theta})} \ {r} \ {dr} \ {d{\theta}} = \displaystyle\int_{\theta=\alpha}^{\theta=\beta}\displaystyle\int_{r=a}^{r=b}f(r,\theta)r \ dr \ d\theta}[/latex].
If the base of the solid can be described as [latex]{D} = {\left \{{(r,{\theta})}{\mid}{\alpha} \ {\leq} \ {\theta} \ {\leq} \ {{\beta},{h_1}}{(\theta)} \ {\leq} \ {r} \ {\leq} \ {h_2{(\theta)}} \right \}}[/latex], then the double integral for the volume becomes
[latex]\large{{V} = \underset{D}{\displaystyle\iint}{f}{(r,{\theta})} \ {r} \ {dr} \ {d{\theta}} = \displaystyle\int_{\theta=\alpha}^{\theta=\beta}\displaystyle\int_{r=h_1(\theta)}^{r=h_2(\theta)}f(r,\theta)r \ dr \ d\theta}[/latex]
We illustrate this idea with some examples.
Example: finding a volume using a double integral
Find the volume of the solid that lies under the paraboloid [latex]z=1-x^{2}-y^{2}[/latex] and above the unit circle on the [latex]xy[/latex]-plane (see the following figure).

Figure 1. The paraboloid [latex]z=1-x^{2}-y^{2}[/latex].
Show Solution
By the method of double integration, we can see that the volume is the iterated integral of the form [latex]\underset{R}{\displaystyle\iint}{(1-{x^2}-{y^2})}{dA}[/latex] where [latex]{R} = {\left \{{(r,{\theta})}{\mid}{0} \ {\leq} \ {r} \ {\leq} \ {{1},{0}} \ {\leq} \ {\theta} \ {\leq} \ {2{\pi}} \right \}}[/latex].
This integration was shown before in Example “Evaluating a Double Integral by Converting from Rectangular Coordinates”, so the volume is [latex]{\frac{\pi}{2}}[/latex] cubic units.
Example: finding a volume using double integration
Find the volume of the solid that lies under the paraboloid [latex]{z} = {4} - {x^2} - {y^2}[/latex] and above the disk [latex]{(x-1)^2} + {y^2} = {1}[/latex] on the [latex]xy[/latex]-plane. See the paraboloid in Figure 2 intersecting the cylinder [latex]{(x-1)^2} + {y^2} = {1}[/latex] above the [latex]xy[/latex]-plane.

Figure 2. Finding the volume of a solid with a paraboloid cap and a circular base.
Show Solution
First change the disk [latex]{(x-1)^2} + {y^2} = {1}[/latex] to polar coordinates. Expanding the square term, we have [latex]{x^2} - {2x} + {1} + {y^2} = {1}[/latex]. Then simplify to get [latex]{x^2} + {y^2} = {2x}[/latex], which in polar coordinates becomes [latex]{r^2} = {2r}{\cos}{\theta}[/latex] and then either [latex]{r} = {0}[/latex] or [latex]{r} = {2}{\cos}{\theta}[/latex]. Similarly, the equation of the paraboloid changes to [latex]{z} = {4} - {r^2}[/latex]. Therefore we can describe the disk [latex]{(x-1)^2} + {y^2} = {1}[/latex] on the [latex]xy[/latex]-plane as the region
[latex]{D} = {\left \{{(r,{\theta})}{\mid}{0} \ {\leq} \ {\theta} \ {\leq} \ {{\pi},{0}} \ {\leq} \ {r} \ {\leq} \ {2{\cos}{\theta}} \right \}}[/latex].
Hence the volume of the solid bounded above by the paraboloid [latex]{z} = {4} - {x^2} - {y^2}[/latex] and below by [latex]{r} = {2}{\cos}{\theta}[/latex] is
[latex]\hspace{3cm}\begin{align} V&=\underset{D}{\displaystyle\iint}f(r,\theta)r \ dr \ d\theta =\displaystyle\int_{\theta=0}^{\theta=\pi}\displaystyle\int_{r=0}^{r=2\cos\theta}(4-r^2)r \ dr \ d\theta \\ &=\displaystyle\int_{\theta=0}^{\theta=\pi}\left[4\frac{r^2}2-\frac{r^4}4\Bigg|_{r=0}^{r=2\cos\theta}\right]d\theta \\ &=\displaystyle\int_{0}^{\pi}[8\cos^2\theta-4\cos^2\theta]d\theta=\left[\frac52\theta+\frac52\sin\theta\cos\theta-\sin\theta\cos^3\theta\right]_0^{\pi}=\frac52\pi \end{align}[/latex].
Notice in the next example that integration is not always easy with polar coordinates. Complexity of integration depends on the function and also on the region over which we need to perform the integration. If the region has a more natural expression in polar coordinates or if [latex]f[/latex] has a simpler antiderivative in polar coordinates, then the change in polar coordinates is appropriate; otherwise, use rectangular coordinates.
Example: finding a volume using a double integral
Find the volume of the region that lies under the paraboloid [latex]z=x^{2}+y^{2}[/latex] and above the triangle enclosed by the lines [latex]y=x[/latex], [latex]x=0[/latex] and [latex]x+y=2[/latex] in the [latex]xy[/latex]-plane (Figure 3).
Show Solution
First examine the region over which we need to set up the double integral and the accompanying paraboloid.

Figure 3. Finding the volume of a solid under a paraboloid and above a given triangle.
The region [latex]D[/latex] is [latex]{\left \{{(x,y)}{\mid}{0} \ {\leq} \ {x} \ {\leq} \ {1,x} \ {\leq} \ {y} \ {\leq} \ {2-x} \right \}}[/latex]. Converting the lines [latex]y=x[/latex], [latex]x=0[/latex], and [latex]x+y=2[/latex] in the [latex]xy[/latex]-plane to functions of [latex]r[/latex] and [latex]\theta[/latex], we have [latex]{{\theta} = {\pi}/{4}}, \ {{\theta} = {\pi}/{2}},[/latex] and [latex]{r} = {2}/{({cos}{\theta}+{sin}{\theta})}[/latex], respectively. Graphing the region on the [latex]xy[/latex]-plane, we see that it looks like [latex]{D}= {\left \{{(r,{\theta})}{\mid}{{\pi}/{4}} \ {\leq} \ {\theta} \ {\leq} \ {{\pi}/{2},0} \ {\leq} \ {r} \ {\leq} \ {2/{({\cos}{\theta}+{\sin}{\theta})}} \right \}}[/latex]. Now converting the equation of the surface gives [latex]{z} = {x^2} + {y^2} = {r^2}[/latex]. Therefore, the volume of the solid is given by the double integral
[latex]\hspace{2cm}\begin{align} V&=\underset{D}{\displaystyle\iint}f(r,\theta)r \ dr \ d\theta=\displaystyle\int_{\theta=\pi/4}^{\theta=\pi/2}\displaystyle\int_{r=0}^{r=2/(\cos\theta+\sin\theta}r^2r \ dr \ d\theta=\displaystyle\int_{\pi/4}^{\pi/2}\left[\frac{r^4}4\right]_{0}^{2/(\cos\theta+\sin\theta)} \ d\theta \\ &=\frac14\displaystyle\int_{\pi/4}^{\pi/2}\left(\frac2{(\cos\theta+\sin\theta)}\right)^4 \ d\theta = \frac{16}4\displaystyle\int_{\pi/4}^{\pi/2}\left(\frac1{(\cos\theta+\sin\theta)}\right)^4 \ d\theta =4\displaystyle\int_{\pi/4}^{\pi/2}\left(\frac1{(\cos\theta+\sin\theta)}\right)^4 \ d\theta. \end{align}[/latex]
As you can see, this integral is very complicated. So, we can instead evaluate this double integral in rectangular coordinates as
[latex]\large{V=\displaystyle\int_0^1\displaystyle\int_x^{2-x}(x^2+y^2)dydx}[/latex].
Evaluating gives
[latex]\hspace{6cm}\begin{align} V&=\displaystyle\int_0^1\displaystyle\int_x^{2-x}(x^2+y^2)dydx=\displaystyle\int_0^1\left[x^2y+\frac{y^3}3\right]\Bigg|_x^{2-x}dx \\ &=\displaystyle\int_0^1\frac83-4x+4x^2-\frac{8x^3}3dx \\ &=\left[\frac{8x}3-2x^2+\frac{4x^3}3-\frac{2x^4}3\right]\bigg|_0^1=\frac43. \end{align}[/latex]
To answer the question of how the formulas for the volumes of different standard solids such as a sphere, a cone, or a cylinder are found, we want to demonstrate an example and find the volume of an arbitrary cone.
Example: finding a volume using a double integral
Use polar coordinates to find the volume inside the cone [latex]{z} = {2} - {\sqrt{{x^2}+{y^2}}}[/latex] and above the [latex]xy[/latex]–plane.
Show Solution
Solution
The region [latex]D[/latex] for the integration is the base of the cone, which appears to be a circle on the [latex]xy[/latex]-plane (see the following figure).

Figure 4. Finding the volume of a solid inside the cone and above the [latex]xy[/latex]-plane.
We find the equation of the circle by setting [latex]z=0[/latex]:
[latex]\hspace{10cm}\large{\begin{align} {0} &= {2} - {\sqrt{{x^2}+{y^2}}} \\ {2} &= {\sqrt{{x^2}+{y^2}}} \\ {x^2} + {y^2} &= {4} \end{align}}[/latex]
This means the radius of the circle is 2, so for the integration we have [latex]{0} \ {\leq} \ {\theta} \ {\leq} \ {2{\pi}}[/latex] and [latex]{0} \ {\leq} \ {r} \ {\leq} \ {2}[/latex]. Substituting [latex]{x} = {r}{cos}{\theta}[/latex] and [latex]{y} = {r}{sin}{\theta}[/latex] in the equation [latex]{z} = {2} - {\sqrt{{x^2}+{y^2}}}[/latex] we have [latex]z=2-r[/latex]. Therefore, the volume of the cone is
[latex]\large{\displaystyle\int_{\theta=0}^{\theta=2\pi}\displaystyle\int_{r=0}^{r=2}(2-r)r \ dr \ d\theta = 2\pi\frac43=\frac{8\pi}3}[/latex] cubic units.
Analysis
Note that if we were to find the volume of an arbitrary cone with radius [latex]a[/latex] and height [latex]h[/latex] units, then the equation of the cone would be [latex]{z} = {h} - {\frac{h}{a}}{\sqrt{{x^2}+{y^2}}}[/latex].
We can still use Figure 4 and set up the integral as [latex]\displaystyle\int_{\theta=0}^{\theta=2\pi}\displaystyle\int_{r=0}^{r=a}\left(h-\frac{h}{a}\right)r \ dr \ d\theta[/latex].
Evaluating the integral, we get [latex]{\frac{1}{3}}{\pi}{a^2}{h}[/latex].
try it
Use polar coordinates to find an iterated integral for finding the volume of the solid enclosed by the paraboloids [latex]{z} = {x^2} + {y^2}[/latex] and [latex]{z} = {16} - {x^2} - {y^2}[/latex].
Show Solution
[latex]V=\displaystyle\int_0^{2\pi}\displaystyle\int_0^{2\sqrt2}(16-2r^2)r \ dr \ d\theta=64\pi[/latex] cubic units.
As with rectangular coordinates, we can also use polar coordinates to find areas of certain regions using a double integral. As before, we need to understand the region whose area we want to compute. Sketching a graph and identifying the region can be helpful to realize the limits of integration. Generally, the area formula in double integration will look like
[latex]\large{\text{Area }A = \displaystyle\int_\alpha^\beta\displaystyle\int_{h_1(\theta)}^{h_2(\theta)}{1r} \ {dr} \ {d{\theta}}}[/latex].
Example: finding an area using a double integral in polar coordinates
Evaluate the area bounded by the curve [latex]{r} = {\cos}{4}{\theta}[/latex].
Show Solution
Sketching the graph of the function [latex]{r} = {\cos}{4}{\theta}[/latex] reveals that it is a polar rose with eight petals (see the following figure).

Figure 5. Finding the area of a polar rose with eight petals.
Using symmetry, we can see that we need to find the area of one petal and then multiply it by 8. Notice that the values of [latex]\theta[/latex] for which the graph passes through the origin are the zeros of the function [latex]{\cos}{4}{\theta}[/latex], and these are odd multiples of [latex]{\pi}/{8}[/latex]. Thus, one of the petals corresponds to the values of [latex]\theta[/latex] in the interval [latex][{{-\pi}/{8}},{{\pi}/{8}}][/latex]. Therefore, the area bounded by the curve [latex]{r} = {\cos}{4}{\theta}[/latex] is
[latex]\begin{align}
A&=8\displaystyle\int_{\theta=-\pi/8}^{\theta=\pi/8}\displaystyle\int_{r=0}^{r=\cos4\theta}1 r \ dr \ d\theta \\ &=8\displaystyle\int_{-\pi/8}^{\pi/8}\left[\frac12r^2\bigg|_{0}^{\cos4\theta}\right]d\theta=8\displaystyle\int_{-\pi/8}^{\pi/8}\frac12\cos^2{4}\theta \ d\theta=8\left[\frac14\theta+\frac1{16}\sin4\theta\cos4\theta\bigg|_{-\pi/8}^{\pi/8}\right]=8[\frac{\pi}{16}]=\frac{\pi}2. \end{align}[/latex]
Example: finding area between two polar curves
Find the area enclosed by the circle [latex]{r} = {3}{\cos}{\theta}[/latex] and the cardioid [latex]{r} = {1} + {\cos}{\theta}[/latex].
Show Solution
First and foremost, sketch the graphs of the region (Figure 6).
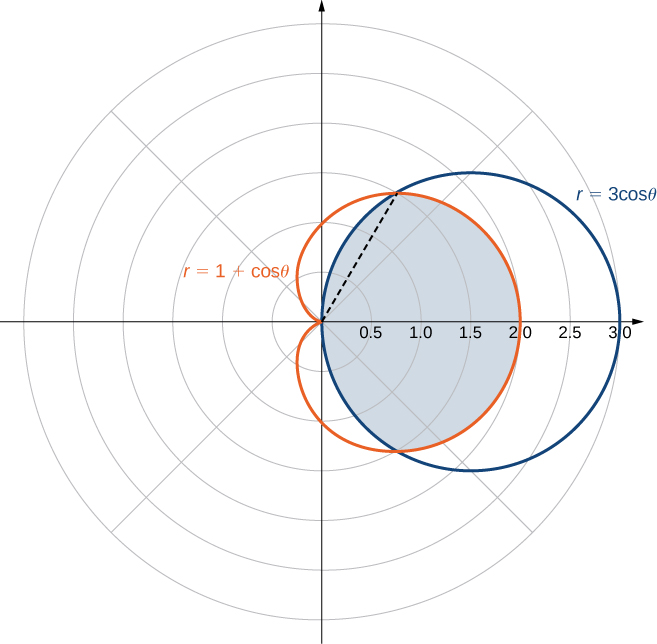
Figure 6. Finding the area enclosed by both a circle and a cardioid.
We can from see the symmetry of the graph that we need to find the points of intersection. Setting the two equations equal to each other gives
[latex]{3}{cos}{\theta} = {1} + {\cos}{\theta}[/latex].
One of the points of intersection is [latex]{\theta} = {{\pi}/{3}}[/latex]. The area above the polar axis consists of two parts, with one part defined by the cardioid from [latex]{\theta} = {0}[/latex] to [latex]{\theta} = {{\pi}/{3}}[/latex] and the other part defined by the circle from [latex]{\theta} = {{\pi}/{3}}[/latex] to [latex]{\theta} = {{\pi}/{2}}[/latex]. By symmetry, the total area is twice the area above the polar axis. Thus, we have
[latex]\large{A=2\left[\displaystyle\int_{\theta=0}^{\theta=\pi/3}\displaystyle\int_{r=0}^{r=1+\cos\theta}1r \ dr \ d\theta+\displaystyle\int_{\theta=\pi/3}^{\theta=\pi/2}\displaystyle\int_{r=0}^{r=3\cos\theta}1r \ dr \ d\theta\right]}[/latex].
Evaluating each piece separately, we find that the area is
[latex]{A} = {2}{\left ({{\frac{1}{4}}{\pi}} + {{\frac{9}{16}}{\sqrt{3}}} + {{\frac{3}{8}}{\pi}} - {{\frac{9}{16}}{\sqrt{3}}} \right)} = {2}{\left ({\frac{5}{8}}{\pi} \right )} = {{\frac{5}{4}}{\pi}}[/latex] square units.
try it
Find the area enclosed inside the cardioid [latex]{r} = {3} - {{3}{\sin}{\theta}}[/latex] and outside the cardioid [latex]{r} = {1} + {{\sin}{\theta}}[/latex].
Show Solution
[latex]A=2\displaystyle\int_{-\pi/2}^{\pi/6}\displaystyle\int_{1+\sin\theta}^{3-3\sin\theta}r \ dr \ d\theta = 8\pi+9\sqrt3[/latex]
Example: evaluating an improper double integral in polar coordinates
Evaluate the integral [latex]\underset{R^2}{\displaystyle\iint}e^{-10(x^2+y^2)}dx \ dy[/latex].
Show Solution
This is an improper integral because we are integrating over an unbounded region [latex]R^2[/latex]. In polar coordinates, the entire plane [latex]R^2[/latex] can be seen as [latex]{0} \ {\leq} \ {\theta} \ {\leq} \ {{{2}{\pi}},0} \ {\leq} \ {r} \ {\leq} \ {\infty}[/latex].
Using the changes of variables from rectangular coordinates to polar coordinates, we have
[latex]\hspace{3cm}\begin{align} \underset{R^2}{\displaystyle\iint}e^{-10(x^2+y^2)}dx \ dy&=\displaystyle\int_{\theta=0}^{\theta=2\pi}\displaystyle\int_{r=0}^{r=\infty}e^{-10r^2}r \ dr \ d\theta=\displaystyle\int_{\theta=0}^{\theta=2\pi}\left(\displaystyle\lim_{a\to\infty}\displaystyle\int_{r=0}^{r=a}e^{-10r^2}r \ dr\right)d\theta \\ &=\left(\displaystyle\int_{\theta=0}^{\theta=2\pi}d\theta\right)\left(\displaystyle\lim_{a\to\infty}\displaystyle\int_{r=0}^{r=a}e^{-10r^2}r \ dr\right) \\ &=2\pi\left(\displaystyle\lim_{a\to\infty}\displaystyle\int_{r=0}^{r=a}e^{-10r^2}r \ dr\right) \\ &=2\pi\displaystyle\lim_{a\to\infty}\left(-\frac1{20}\right)\left(e^{-10r^2}\bigg|_0^1\right)\\ &=2\pi\left(-\frac1{20}\right)\displaystyle\lim_{a\to\infty}\left(e^{-10a^2}-1\right)\\ &=\frac{\pi}{10} \end{align}[/latex]
try it
Evaluate the integral [latex]\underset{R^2}{\displaystyle\iint}{e^{{-4}{(x^2+y^2)}}}{dx^{}}{dy}[/latex].
Show Solution
[latex]\frac{\pi}4[/latex]
Watch the following video to see the worked solution to the above Try It
Candela Citations
CC licensed content, Original
CC licensed content, Shared previously






