Projections and Work

Learning Objectives

Explain what is meant by the vector projection of one vector onto another vector, and describe how to compute it.
Calculate the work done by a given force.

Projections

As we have seen, addition combines two vectors to create a resultant vector. But what if we are given a vector and we need to find its component parts? We use vector projections to perform the opposite process; they can break down a vector into its components. The magnitude of a vector projection is a scalar projection. For example, if a child is pulling the handle of a wagon at a $55^\circ$ angle, we can use projections to determine how much of the force on the handle is actually moving the wagon forward (Figure 1). We return to this example and learn how to solve it after we see how to calculate projections.

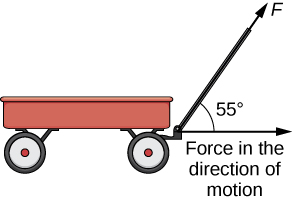
This figure is the image of a wagon with a handle. The handle is represented by the vector “F.” The angle between F and the horizontal direction of the wagon is 55 degrees.

Figure 1. When a child pulls a wagon, only the horizontal component of the force propels the wagon forward.

DEFINITION

The vector projection of $\mathbf{v}$ onto $\mathbf{u}$ is the vector labeled $\text{proj}_\text{u}\mathbf{v}$ in Figure 2. It has the same initial point as $\mathbf{u}$ and $\mathbf{v}$ and the same direction as $\mathbf{u}$ , and represents the component of $\mathbf{v}$ that acts in the direction of $\mathbf{u}$ . If $\theta$ represents the angle between $\mathbf{u}$ and $\mathbf{v}$ , then, by properties of triangles, we know the length of $\text{proj}_\text{u}\mathbf{v}$ is $||\text{proj}_\text{u}\mathbf{v}|| = ||\mathbf{v}||\cos{\theta}$ . When expressing $\cos{\theta}$ in terms of the dot product, this becomes

\begin{aligned} | | {proj}_{u} v | | & = | | v | | \cos θ \\ = | | v | | (\frac{| u \cdot v |}{| | u | | | | v | |}) \\ = \frac{| u \cdot v |}{| | u | |} . \end{aligned}

$\begin{align*} ||\text{proj}_\text{u}\mathbf{v}|| &= ||\mathbf{v}||\cos{\theta}\\ &= ||\mathbf{v}||(\frac{|\mathbf{u}\cdot\mathbf{v}|}{||\mathbf{u}||\,||\mathbf{v}||})\\ &= \frac{|\mathbf{u}\cdot\mathbf{v}|}{||\mathbf{u}||}.\\\end{align*}$

We now multiply by a unit vector in the direction of $\mathbf{u}$ to get $\text{proj}_\text{u}\mathbf{v}$ :

{proj}_{u} v = \frac{| u \cdot v |}{| | u | |} (\frac{1}{| | u | |} u) = \frac{u \cdot v}{| | u | |^{2}} u

$\text{proj}_\text{u}\mathbf{v} = \frac{|\mathbf{u}\cdot\mathbf{v}|}{||\mathbf{u}||}(\frac{1}{||\mathbf{u}||}\mathbf{u}) = \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{u}||^2}\mathbf{u}$ .

The length of this vector is also known as the scalar projection of $\mathbf{v}$ onto $\mathbf{u}$ and is denoted by

| | {proj}_{u} v | | = | | {comp}_{u} v | | = \frac{| u \cdot v |}{| | u | |}

$||\text{proj}_\text{u}\mathbf{v}|| = ||\text{comp}_\text{u}\mathbf{v}|| = \frac{|\mathbf{u}\cdot\mathbf{v}|}{||\mathbf{u}||}$ .

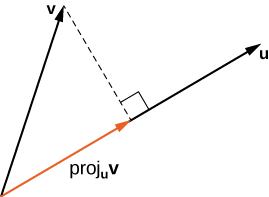
This image has a vector labeled “v.” There is also a vector with the same initial point labeled “proj sub u v.” The third vector is from the terminal point of proj sub u v in the same direction labeled “u.” A broken line segment from the initial point of u to the terminal point of v is drawn and is perpendicular to u.

Figure 2. The projection of ${\bf{v}}$ onto ${\bf{u}}$ shows the component of vector ${\bf{v}}$ in the direction of ${\bf{u}}$ .

Example: finding projections

Find the projection of $\mathbf{v}$ onto $\mathbf{u}$ .

$\mathbf{v} = \langle 3,5,1 \rangle$ and $\mathbf{u} = \langle -1,4,3 \rangle$
$\mathbf{v} = 3\mathbf{i} -2\mathbf{j}$ and $\mathbf{u} = \mathbf{i} +6\mathbf{j}$

Show Solution

Substitute the components of $\mathbf{v}$ and $\mathbf{u}$ into the formula for the projection:
$\begin{align*} \text{proj}_\text{u}\mathbf{v} &= \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{u}||^2}\mathbf{u}\\ &= \frac{\langle -1,4,3 \rangle \cdot \langle 3,5,1 \rangle}{||\langle -1,4,3 \rangle||^2}\langle -1,4,3 \rangle\\ &= \frac{-3+20+3}{(-1)^2+4^2+3^2}\langle -1,4,3 \rangle\\ &= \frac{20}{26}\langle -1,4,3 \rangle\\ &= \langle -\frac{10}{13},\frac{40}{13},\frac{30}{13} \rangle.\\\end{align*}$
To find the two-dimensional projection, simply adapt the formula to the two-dimensional case:
$\begin{align*} \text{proj}_\text{u}\mathbf{v} &= \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{u}||^2}\mathbf{u}\\ &= \frac{(\mathbf{i} +6\mathbf{j}) \cdot ( 3\mathbf{i} -2\mathbf{j})}{||\mathbf{i} +6\mathbf{j}||^2}(\mathbf{i} +6\mathbf{j})\\ &= \frac{1(3)+6(-2)}{1^2+6^2}(\mathbf{i} +6\mathbf{j})\\ &= -\frac{9}{37}(\mathbf{i} +6\mathbf{j})\\ &= -\frac{9}{37}\mathbf{i}- \frac{54}{37}\mathbf{j}.\\\end{align*}$

Try It

Sometimes it is useful to decompose vectors—that is, to break a vector apart into a sum. This process is called the resolution of a vector into components. Projections allow us to identify two orthogonal vectors having a desired sum. For example, let $\mathbf{v} = \langle 6,-4 \rangle$ and let $\mathbf{u} = \langle 3,1 \rangle$ . We want to decompose the vector $\mathbf{v}$ into orthogonal components such that one of the component vectors has the same direction as $\mathbf{u}$ .

We first find the component that has the same direction as $\mathbf{u}$ by projecting $\mathbf{v}$ onto $\mathbf{u}$ . Let $\mathbf{p} = \text{proj}_\text{u}\mathbf{v}$ . Then, we have

\begin{aligned} p & = \frac{u \cdot v}{| | u | |^{2}} u \\ = \frac{18 - 4}{9 + 1} u \\ = \frac{7}{5} u = \frac{7}{5} ⟨ 3, 1 ⟩ = ⟨ \frac{21}{5}, \frac{7}{5} ⟩ . \end{aligned}

$\begin{align*} \mathbf{p} &= \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{u}||^2}\mathbf{u}\\ &= \frac{18-4}{9+1}\mathbf{u}\\ &= \frac{7}{5}\mathbf{u} = \frac{7}{5} \langle 3,1 \rangle = \langle \frac{21}{5},\frac{7}{5} \rangle.\\\end{align*}$

Now consider the vector $\mathbf{q} = \mathbf{v} - \mathbf{p}$ . We have

\begin{aligned} q & = v - p \\ = ⟨ 6, - 4 ⟩ - ⟨ \frac{21}{5}, \frac{7}{5} ⟩ \\ = ⟨ \frac{9}{5}, - \frac{27}{5} ⟩ . \end{aligned}

$\begin{align*} \mathbf{q} &= \mathbf{v} - \mathbf{p}\\ &= \langle 6,-4 \rangle - \langle \frac{21}{5},\frac{7}{5} \rangle\\ &= \langle \frac{9}{5},-\frac{27}{5} \rangle.\\\end{align*}$

Clearly, by the way we defined $\mathbf{q}$ , we have $\mathbf{v} = \mathbf{q} + \mathbf{p}$ , and

\begin{aligned} q \cdot p & = ⟨ \frac{9}{5}, - \frac{27}{5} ⟩ \cdot ⟨ \frac{21}{5}, \frac{7}{5} ⟩ \\ = \frac{9 (21)}{25} + \frac{- 27 (7)}{25} \\ = \frac{189}{25} - \frac{189}{25} = 0 . \end{aligned}

$\begin{align*} \mathbf{q} \cdot \mathbf{p} &= \langle \frac{9}{5},-\frac{27}{5} \rangle \cdot \langle \frac{21}{5},\frac{7}{5} \rangle\\ &= \frac{9(21)}{25}+\frac{-27(7)}{25} \\ &= \frac{189}{25}-\frac{189}{25} = 0 .\\\end{align*}$

Therefore, $\mathbf{q}$ and $\mathbf{p}$ are orthogonal.

Example: resolving vectors into components

Express $\mathbf{v} = \langle 8,-3,-3 \rangle$ as a sum of orthogonal vectors such that one of the vectors has the same direction as $\mathbf{u} = \langle 2,3,2 \rangle$ .

Show Solution

Let $\mathbf{p}$ represent the projection of $\mathbf{v}$ onto $\mathbf{u}$ :

\begin{aligned} p & = {proj}_{u} v \\ = \frac{u \cdot v}{| | u | |^{2}} u \\ = \frac{⟨ 2, 3, 2 ⟩ \cdot ⟨ 8, - 3, - 3 ⟩}{| | ⟨ 2, 3, 2 ⟩ | |^{2}} ⟨ 2, 3, 2 ⟩ \\ = \frac{16 - 9 - 6}{2^{2} + 3^{2} + 2^{2}} ⟨ 2, 3, 2 ⟩ \\ = \frac{1}{17} ⟨ 2, 3, 2 ⟩ \\ = ⟨ \frac{2}{17}, \frac{3}{17}, \frac{2}{17} ⟩ . \end{aligned}

$\begin{align*} \mathbf{p} & = \text{proj}_\text{u}\mathbf{v}\\ &= \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{u}||^2}\mathbf{u} \\ &=\frac{\langle 2,3,2 \rangle \cdot \langle 8,-3,-3 \rangle}{||\langle 2,3,2 \rangle||^2}\langle 2,3,2 \rangle \\ &= \frac{16-9-6}{2^2+3^2+2^2}\langle 2,3,2 \rangle\\ &= \frac{1}{17}\langle 2,3,2 \rangle\\ &= \langle \frac{2}{17},\frac{3}{17},\frac{2}{17} \rangle.\\\end{align*}$

Then,

q = v - p = ⟨ 8, - 3, - 3 ⟩ - ⟨ \frac{2}{17}, \frac{3}{17}, \frac{2}{17} ⟩ = ⟨ \frac{134}{17}, - \frac{54}{17}, - \frac{53}{17} ⟩ .

$\mathbf{q} =\mathbf{v} - \mathbf{p} = \langle 8,-3,-3 \rangle - \langle \frac{2}{17},\frac{3}{17},\frac{2}{17} \rangle = \langle \frac{134}{17},-\frac{54}{17},-\frac{53}{17} \rangle.$

To check our work, we can use the dot product to verify that $\textbf p$ and $\textbf q$ are orthogonal vectors:

p \cdot q = ⟨ \frac{2}{17}, \frac{3}{17}, \frac{2}{17} ⟩ \cdot ⟨ \frac{134}{17}, - \frac{54}{17}, - \frac{53}{17} ⟩ = \frac{268}{289} - \frac{162}{289} - \frac{106}{289} = 0

$\mathbf{p} \cdot \mathbf{q} = \langle \frac{2}{17},\frac{3}{17},\frac{2}{17} \rangle \cdot \langle \frac{134}{17},-\frac{54}{17},-\frac{53}{17} \rangle = \frac{268}{289} - \frac{162}{289}-\frac{106}{289} = 0$ .

Then,

v = p + q = ⟨ \frac{2}{17}, \frac{3}{17}, \frac{2}{17} ⟩ + ⟨ \frac{134}{17}, - \frac{54}{17}, - \frac{53}{17} ⟩

$\mathbf{v} = \mathbf{p} + \mathbf{q} = \langle \frac{2}{17},\frac{3}{17},\frac{2}{17} \rangle + \langle \frac{134}{17},-\frac{54}{17},-\frac{53}{17} \rangle$ .

try it

Express $\mathbf{v} = 5\mathbf{i} - \mathbf{j}$ as a sum of orthogonal vectors such that one of the vectors has the same direction as $\mathbf{u} = 4\mathbf{i} +2\mathbf{j}$ .

Show Solution

$\mathbf{v} = \mathbf{p} + \mathbf{q}$ , where $\mathbf{p} = \frac{18}{5}\mathbf{i} + \frac{19}{5}\mathbf{j}$ and $\mathbf{q} = \frac{7}{5}\mathbf{i} - \frac{14}{5}\mathbf{j}$

Watch the following video to see the worked solution to the above Try IT.

You can view the transcript for “CP 2.27” here (opens in new window).

Example: scalar projection of velocity

A container ship leaves port traveling $15^\circ$ north of east. Its engine generates a speed of $20$ knots along that path (see the following figure). In addition, the ocean current moves the ship northeast at a speed of 2 knots. Considering both the engine and the current, how fast is the ship moving in the direction $15^\circ$ north of east? Round the answer to two decimal places.

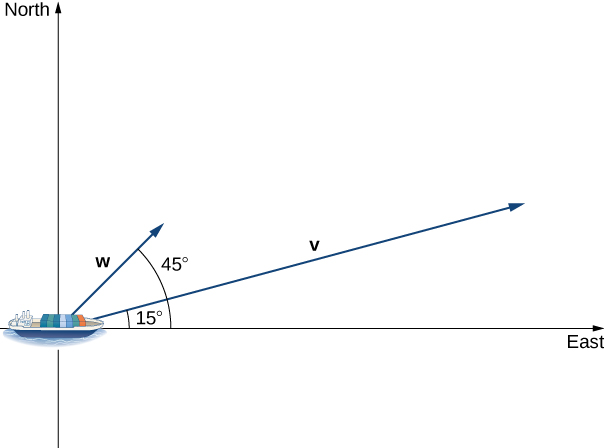
This figure is an image of a ship. The ship is at the origin of two perpendicular axes. The horizontal axis is labeled “east.” The second axis is vertical and labeled “north.” From the ship there are two vectors. The first is labeled “v” and has an angle of 15 degrees between the East axis and the vector v. The second vector is labeled “w” and has an angle of 45 degrees between the East axis and the vector w.

Figure 3. Find how fast the ship is moving in the direction of $15^{\circ}$ north of east.

Show Solution

Let $\mathbf{v}$ be the velocity vector generated by the engine, and let $\mathbf{w}$ be the velocity vector of the current. We already know $||\mathbf{v}|| = 20$ along the desired route. We just need to add in the scalar projection of $\mathbf{w}$ onto $\mathbf{v}$ . We get

\begin{aligned} {comp}_{v} w & = \frac{v \cdot w}{| | v | |} \\ = \frac{| | v | | | | w | | \cos (30^{\circ})}{| | v | |} \\ = | | w | | \cos (30^{\circ}) \\ = 2 \frac{\sqrt{3}}{2} = \sqrt{3} \approx 1.73 knots. \end{aligned}

$\begin{align*} \text{comp}_\text{v}\mathbf{w} &= \frac{\mathbf{v} \cdot \mathbf{w}}{||\mathbf{v}||}\\ &= \frac{||\mathbf{v}|| \, ||\mathbf{w}||\cos{(30^\circ)}}{||\mathbf{v}||}\\ &=||\mathbf{w}||\cos{(30^\circ)} \\ &= 2\frac{\sqrt{3}}{2} = \sqrt{3} \approx 1.73 \text{ knots.}\\\end{align*}$

The ship is moving at 21.73 knots in the direction $15^\circ$ north of east.

try it

Repeat the previous example, but assume the ocean current is moving southeast instead of northeast, as shown in the following figure.

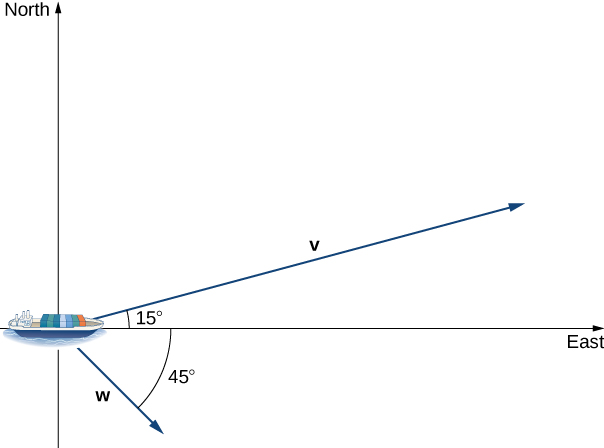
Figure 4. Find how fast the ship is moving in the direction $45^{\circ}$ south of east.

Show Solution

$21$ knots.

Work

Now that we understand dot products, we can see how to apply them to real-life situations. The most common application of the dot product of two vectors is in the calculation of work.

From physics, we know that work is done when an object is moved by a force. When the force is constant and applied in the same direction the object moves, then we define the work done as the product of the force and the distance the object travels: $W=Fd$ . We saw several examples of this type in earlier chapters. Now imagine the direction of the force is different from the direction of motion, as with the example of a child pulling a wagon. To find the work done, we need to multiply the component of the force that acts in the direction of the motion by the magnitude of the displacement. The dot product allows us to do just that. If we represent an applied force by a vector F and the displacement of an object by a vector s, then the work done by the force is the dot product of F and s.

DEFINITION

When a constant force is applied to an object so the object moves in a straight line from point $P$ to point $Q$ , the work $W$ done by the force F, acting at an angle $\theta$ from the line of motion, is given by

W = F \cdot \vec{P Q} = | | F | | | | \vec{P Q} | | \cos θ

$W = \mathbf{F} \cdot \overrightarrow{PQ} = ||\mathbf{F}||\,||\overrightarrow{PQ}||\cos{\theta}$ .

Let’s revisit the problem of the child’s wagon introduced earlier. Suppose a child is pulling a wagon with a force having a magnitude of $8$ lb on the handle at an angle of $55^\circ$ . If the child pulls the wagon $50$ ft, find the work done by the force (Figure 5).

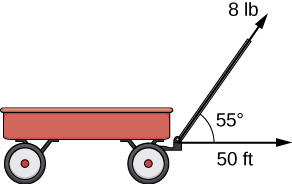
This figure is an image of a wagon with a handle. The handle is represented with a vector labeled “8 lb.” There is another vector in the horizontal direction from the wagon labeled “50 ft.” The angle between these vectors is 55 degrees.

Figure 5. The horizontal component of the force is the projection of ${\bf{F}}$ onto the positive $x$ -axis.

We have

W = | | F | | | | \vec{P Q} | | \cos θ = 8 (50) (\cos (55^{\circ})) \approx 229 ft \cdot lb

$W = ||\mathbf{F}||\,||\overrightarrow{PQ}||\cos{\theta} = 8(50)(\cos{(55^\circ)}) \approx 229 \text{ft} \cdot \text{lb}$ .

In U.S. standard units, we measure the magnitude of force $||\mathbf{F}||$ in pounds. The magnitude of the displacement vector $||\overrightarrow{PQ}||$ tells us how far the object moved, and it is measured in feet. The customary unit of measure for work, then, is the foot-pound. One foot-pound is the amount of work required to move an object weighing $1$ lb a distance of $1$ ft straight up. In the metric system, the unit of measure for force is the newton (N), and the unit of measure of magnitude for work is a newton-meter (N·m), or a joule (J).

Example: calculating work

A conveyor belt generates a force $\mathbf{F} = 5\mathbf{i} - 3\mathbf{j} + \mathbf{k}$ that moves a suitcase from point $(1, 1, 1)$ to point $(9, 4, 7)$ along a straight line. Find the work done by the conveyor belt. The distance is measured in meters and the force is measured in newtons.

Show Solution

The displacement vector $\overrightarrow{PQ}$ has initial point $(1, 1, 1)$ and terminal point $(9, 4, 7)$ :

\vec{P Q} = ⟨ 9 - 1, 4 - 1, 7 - 1 ⟩ = ⟨ 8, 3, 6 ⟩ = 8 i + 3 j + 6 k

$\overrightarrow{PQ} = \langle 9-1,4-1,7-1\rangle = \langle 8,3,6 \rangle = 8\mathbf{i} +3\mathbf{j} +6\mathbf{k}$ .

Work is the dot product of force and displacement:

\begin{aligned} W & = F \cdot \vec{P Q} \\ = (5 i - 3 j + k) \cdot (8 i + 3 j + 6 k) \\ = 5 (8) + (- 3) (3) + 1 (6) \\ = 37 N \cdot m \\ = 37 J. \end{aligned}

$\begin{align*} W &= \mathbf{F} \cdot \overrightarrow{PQ}\\ &= (5\mathbf{i} - 3\mathbf{j} + \mathbf{k}) \cdot (8\mathbf{i} +3\mathbf{j} +6\mathbf{k})\\ &=5(8) + (-3)(3)+1(6) \\ &= 37 \text{N} \cdot \text{m}\\ &= 37 \text{J.} \\\end{align*}$

try it

A constant force of $30$ lb is applied at an angle of $60^\circ$ to pull a handcart $10$ ft across the ground (Figure 6). What is the work done by this force?

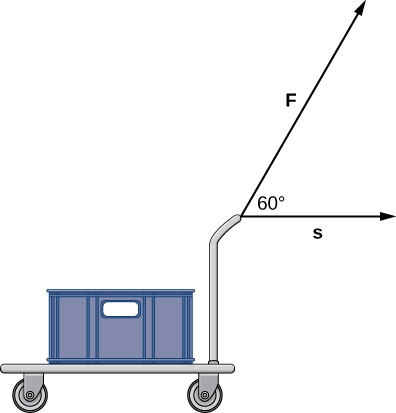
This figure is an image of a hand cart with a crate. The vertical handle of the hand cart has two vectors. The first is horizontal to the handle and labeled “s.” The second is from the handle and labeled “F.” The angle between the two vectors is 60 degrees.

Figure 6. Find the force ${\bf{F}}$ .

Show Solution

$150$ ft-lb

Module 2: Vectors in Space

Learning Objectives

Projections

DEFINITION

Example: finding projections

Try It

Example: resolving vectors into components

try it

Example: scalar projection of velocity

try it

Work

DEFINITION

Example: calculating work

try it

Try It

Candela Citations