Putting It Together: Differentiation of Functions of Several Variables

Profitable Golf Balls

Figure 1.

Pro-[latex]T[/latex] company has developed a profit model that depends on the number [latex]x[/latex] of golf balls sold per month (measured in thousands), and the number of hours per month of advertising [latex]y[/latex], according to the function

[latex]z=f(x,y)=48x+96y-x^{2}-2xy-9y^{2}[/latex]

where [latex]z[/latex] is measured in thousands of dollars. The maximum number of golf balls that can be produced and sold is [latex]50,000[/latex], and the maximum number of hours of advertising that can be purchased is [latex]25[/latex]. Find the values of [latex]x[/latex] and [latex]y[/latex] that maximize profit, and find the maximum profit.

Solution

Using the problem-solving strategy, step 1 involves finding the critical points of [latex]f[/latex] on its domain. Therefore, we first calculate [latex]f_{x}(x,y)[/latex] and [latex]f_{y}(x,y)[/latex], then set them each equal to zero:

[latex]\begin{array}{c}f_{x}(x,y) &=& 48-2x-2y \hfill \\f_{y}(x,y) &=& 96-2x-18y \hfill \end{array}[/latex]

Setting them equal to zero yields the system of equations

[latex]\begin{array}{c}48-2x-2y &=& 0 \hfill \\96-2x-18y &=& 0 \hfill \end{array}[/latex]

The solution to this system is [latex]x=21[/latex] and [latex]y=3[/latex]. Therefore [latex](21,3)[/latex] is a critical point of [latex]f[/latex]. Calculating [latex]f(21,3)[/latex] gives [latex]f(21,3)=48(21)+96(3)-21^{2}-2(21)(3)-9(3)^{2}=648[/latex].

The domain of this function is [latex]0\le{x}\le{50}[/latex] and [latex]0\le{y}\le{25}[/latex] as shown in the following graph.

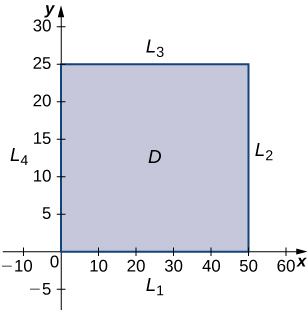
A rectangle is drawn in the first quadrant with one corner at the origin, horizontal length 50, and height 25. This rectangle is marked D, and the sides are marked in counterclockwise order from the side overlapping the x axis L1, L2, L3, and L4.

Figure 2. Graph of the domain of the function[latex]z=f(x,y)=48x+96y-x^{2}-2xy-9y^{2}[/latex].

[latex]L_{1}[/latex] is the line segment connecting [latex](0,0)[/latex] and [latex](50,0)[/latex], and it can be parameterized by the equations [latex]x(t)=t[/latex], [latex]y(t)=0[/latex] for [latex]0\le{t}\le{50}[/latex]. We then define [latex]g(t)=f(x(t),y(t))[/latex]:

[latex]\begin{array}{c}g(t) &=&f(x(t),y(t)) \hfill \\ &=& f(t,0) \hfill \\ &=& 48t+96(0)-y^{2}-2(t)(0)-9(0)^{2} \hfill \\ &=& 48t-t^{2} \hfill \end{array}[/latex]

Setting [latex]g^{\prime}(t)=0[/latex] yields the critical point [latex]t=24[/latex], which corresponds to the point [latex](24,0)[/latex] in the domain of [latex]f[/latex]. Calculating [latex]f(24,0)[/latex] gives [latex]576[/latex].

[latex]L_{2}[/latex] is the line segment connecting [latex](50,0)[/latex] and [latex](50,25)[/latex], and it can be parameterized by the equations [latex]x(t)=50[/latex], [latex]y(t)=t[/latex] for [latex]0\le{t}\le{25}[/latex]. Once again we define [latex]g(t)=f(x(t),y(t))[/latex]:

[latex]\begin{array}{c}g(t) &=&f(x(t),y(t)) \hfill \\ &=& f(50,t) \hfill \\ &=& 48(50)+96t-50^{2}-2(50)t-9t^{2} \hfill \\ &=& -9t^{2}-4t-100 \hfill \end{array}[/latex]

This function has a critical point [latex]t=-\frac{2}{9}[/latex], which corresponds to the point [latex](50,-\frac{2}{9})[/latex]. This point is not in the domain of [latex]f[/latex].

[latex]L_{3}[/latex] is the line segment connecting [latex](0,25)[/latex] and [latex](50,25)[/latex], and it can be parameterized by the equations [latex]x(t)=t[/latex], [latex]y(t)=25[/latex] for [latex]0\le{t}\le{50}[/latex]. We define [latex]g(t)=f(x(t),y(t))[/latex]:

[latex]\begin{array}{c}g(t) &=&f(x(t),y(t)) \hfill \\ &=& f(t,25) \hfill \\ &=& 48(t)+96(25)-t^{2}-2t(25)-9(25)^{2} \hfill \\ &=& -t^{2}-2t-3225 \hfill \end{array}[/latex]

This function has a critical point [latex]t=-1[/latex], which corresponds to the point [latex](-1,25)[/latex], which is not in the domain.

[latex]L_{4}[/latex] is the line segment connecting [latex](0)[/latex] and [latex](0,25)[/latex], and it can be parameterized by the equations [latex]x(t)=0[/latex], [latex]y(t)=t[/latex] for [latex]0\le{t}\le{25}[/latex]. We define [latex]g(t)=f(x(t),y(t))[/latex]:

[latex]\begin{array}{c}g(t) &=&f(x(t),y(t)) \hfill \\ &=& f(0,t) \hfill \\ &=& 48(0)+96t-(0)^{2}-2(0)t-9t^{2} \hfill \\ &=& 96t-t^{2} \hfill \end{array}[/latex]

This function has a critical point [latex]t=\frac{16}{3}[/latex], which corresponds to the point [latex](0,\frac{16}{3})[/latex], which is on the boundary of the domain. Calculating [latex]f(0,\frac{16}{3})[/latex] gives [latex]256[/latex].

We also need to find the values of $f (x, y)$ [latex]f(x,y)[/latex] at the corners of its domain. These corners are located at [latex](0,0),(50,0),(50,25),\text{ and }(0,25)[/latex]:

[latex]\begin{array}{c}f(0,0) &=& 48(0)+96(0)-(0)^{2}-2(0)(0)-9(0)^{2}=0 \hfill \\f(50,0) &=& 48(50)+96(0)-(50)^{2}-2(50)(0)-9(0)^{2}=-100 \hfill \\f(50,25) &=& 48(50)+96(25)-(500)^{2}-2(50)(25)-9(25)^{2}=-5825 \hfill \\f(0,25) &=& 48(0)+96(25)-(0)^{2}-2(0)(25)-9(25)^{2}=-3225 \hfill \end{array}[/latex]

The maximum critical value is [latex]648[/latex] which occurs at [latex](21,3)[/latex]. Therefore, a maximum profit of [latex]\$648,000[/latex] is realized when [latex]21,000[/latex] golf balls are sold and [latex]33[/latex] hours of advertising are purchased per month as shown in the following figure.

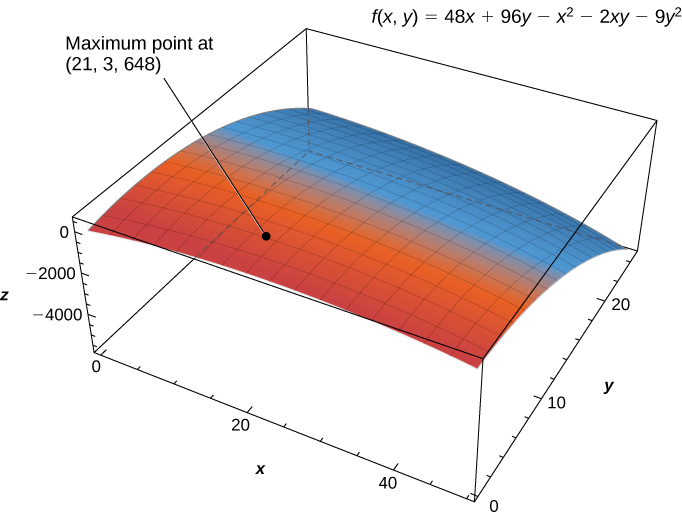
The function f(x, y) = 48x + 96y – x2 – 2xy – 9y2 is shown with maximum point at (21, 3, 648). The shape is a plane curving from near the origin down to (50, 25).

Figure 3. The profit function [latex]f(x,y)[/latex] has a maximum at [latex](21,3,648)[/latex].

Module 4: Differentiation of Functions of Several Variables