Putting It Together: Vector Calculus

Drawing a Rotational Vector Field

A photograph of a hurricane, showing the rotation around its eye.

Figure 1.

Sketch the vector field [latex]{\bf{F}}(x,y)=\langle y,-x\rangle[/latex]

Solution

Create a table (see the one that follows) using a representative sample of points in a plane and their corresponding vectors.

[latex](x,y)[/latex] [latex]{\bf{F}}(x,y)[/latex] [latex](x,y)[/latex] [latex]{\bf{F}}(x,y)[/latex] [latex](x,y)[/latex] [latex]{\bf{F}}(x,y)[/latex]
[latex](1,0)[/latex] [latex]\langle 0,-1\rangle[/latex] [latex](2,0)[/latex] [latex]\langle 0,-2 \rangle[/latex] [latex](1,1)[/latex] [latex]\langle 1,-1\rangle[/latex]
[latex](0,1)[/latex] [latex]\langle 1,0\rangle[/latex] [latex](0,2)[/latex] [latex]\langle 2,0\rangle[/latex] [latex](-1,1)[/latex] [latex]\langle 1,1\rangle[/latex]
[latex](-1,0)[/latex] [latex]\langle 0,1\rangle[/latex] [latex](-2,0)[/latex] [latex]\langle 0,2\rangle[/latex] [latex](-1,-1)[/latex] [latex]\langle -1,1\rangle[/latex]
[latex](0,-1)[/latex] [latex]\langle -1,0\rangle[/latex] [latex](0,-2)[/latex] [latex]\langle -2,0\rangle[/latex] [latex](1,-1)[/latex]  [latex]\langle -1,-1\rangle[/latex]
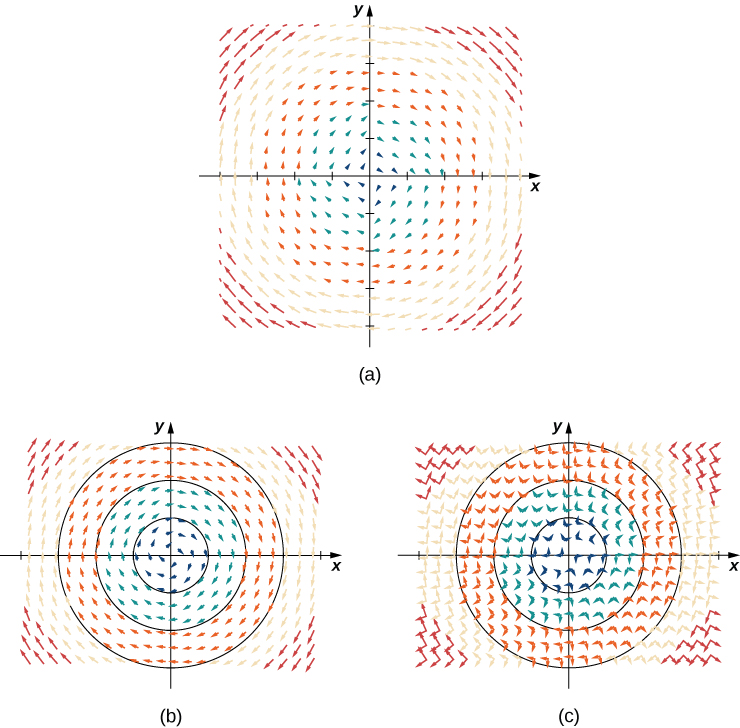
A visual representation of the given vector field in a coordinate plane with two additional diagrams with notation. The first representation shows the vector field. The arrows are circling the origin in a clockwise motion. The second representation shows concentric circles, highlighting the radial pattern. The The third representation shows the concentric circles. It also shows arrows for the radial vector <a,b> for all points (a,b). Each is perpendicular to the arrows in the given vector field.

Figure 2. (a) A visual representation of vector field [latex]{\bf{F}}(x,y)=\langle y,-x\rangle[/latex]. (b) Vector field [latex]{\bf{F}}(x,y)=\langle y,-x\rangle[/latex] with circles centered at the origin. (c) Vector [latex]{\bf{F}}(a,b)[/latex] is perpendicular to radial vector [latex]\langle a,b\rangle[/latex] at point [latex](a,b)[/latex].

Analysis

Note that vector [latex]{\bf{F}}(a,b)=\langle b,-a\rangle[/latex] points clockwise and is perpendicular to radial vector [latex]\langle a,b\rangle[/latex]. (We can verify this assertion by computing the dot product of the two vectors: [latex]\langle a,b\rangle\cdot\langle -b,a\rangle= -ab+ab=0[/latex].) Furthermore, vector [latex]\langle b,-a\rangle[/latex] has length [latex]r=\sqrt{a^{2}+b^{2}}[/latex]. Thus, we have a complete description of this rotational vector field: the vector associated with point [latex](a,b)[/latex] is the vector with length [latex]r[/latex] tangent to the circle with radius [latex]r[/latex], and it points in the clockwise direction.

Sketches such as that in Figure 6 under Example “Sketching a Vector Field” are often used to analyze major storm systems, including hurricanes and cyclones. In the northern hemisphere, storms rotate counterclockwise; in the southern hemisphere, storms rotate clockwise. (This is an effect caused by Earth’s rotation about its axis and is called the Coriolis Effect.)