Finding the Focus of a Parabolic Reflector

Energy hitting the surface of a parabolic reflector is concentrated at the focal point of the reflector (Figure 1). If the surface of a parabolic reflector is described by equation [latex]\frac{x^2}{100}+\frac{y^2}{100}=\frac{z}{4}[/latex], where is the focal point of the reflector?

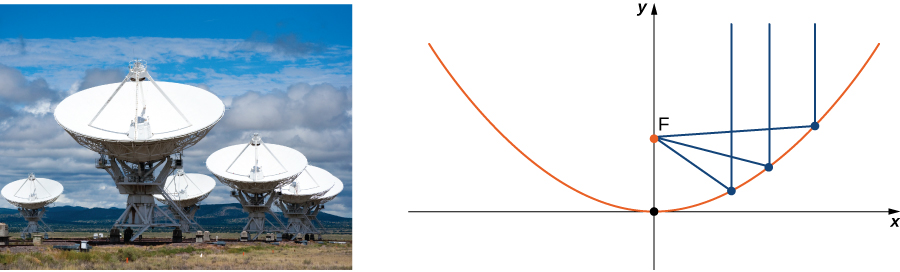
Figure 1. Energy reflects off of the parabolic reflector and is collected at the focal point. (credit: modification of CGP Grey, Wikimedia Commons)

Solution

Since [latex]z[/latex] is the first-power variable, the axis of the reflector corresponds to the [latex]z[/latex]-axis. The coefficients of [latex]x^2[/latex] and [latex]y^2[/latex] are equal, so the cross-section of the paraboloid perpendicular to the [latex]z[/latex]-axis is a circle. We can consider a trace in the [latex]xz[/latex]-plane or the [latex]yz[/latex]-plane; the result is the same. Setting [latex]y=0[/latex], the trace is a parabola opening up along the [latex]z[/latex]-axis, with standard equation [latex]x^2=4pz[/latex], where [latex]p[/latex] is the focal length of the parabola. In this case, this equation becomes [latex]x^2=100\cdot\frac{z}{4}=4pz[/latex] or [latex]25=4p[/latex]. So [latex]p[/latex] is [latex]6.25[/latex] m, which tells us that the focus of the paraboloid is [latex]6.25[/latex] m up the axis from the vertex. Because the vertex of this surface is the origin, the focal point is [latex](0,0,6.25)[/latex].