In earlier sections, we used a unit circle to define the trigonometric functions. In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of [latex]t[/latex] is its value at [latex]t[/latex] radians. First, we need to create our right triangle. Figure 1 shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point [latex]\left(x,y\right)\\[/latex] to the x-axis, we have a right triangle whose vertical side has length [latex]y[/latex] and whose horizontal side has length [latex]x[/latex]. We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

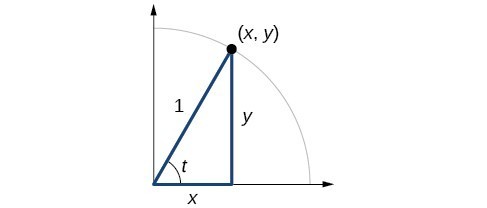
Figure 1

We know

Likewise, we know

These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using [latex]\left(x,y\right)\\[/latex] coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of [latex]x[/latex], we will call the side between the given angle and the right angle the adjacent side to angle [latex]t[/latex]. (Adjacent means “next to.”) Instead of [latex]y[/latex], we will call the side most distant from the given angle the opposite side from angle [latex]\text{}t[/latex]. And instead of [latex]1[/latex], we will call the side of a right triangle opposite the right angle the hypotenuse. These sides are labeled in Figure 2.

Figure 2. The sides of a right triangle in relation to angle [latex]t[/latex].

Understanding Right Triangle Relationships

Given a right triangle with an acute angle of [latex]t[/latex],

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.”

Example 1: Evaluating a Trigonometric Function of a Right Triangle

Given the triangle shown in Figure 3, find the value of [latex]\cos \alpha \\[/latex].

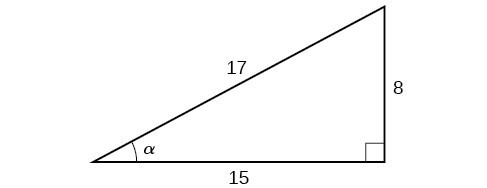
Figure 3

 

Try It 1

Given the triangle shown in Figure 4, find the value of [latex]\text{sin}t[/latex].

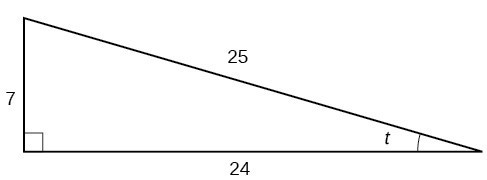
Figure 4

Solution

Relating Angles and Their Functions

When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure 5. The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.

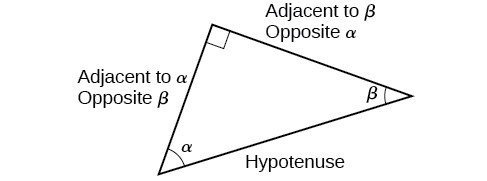
Figure 5. The side adjacent to one angle is opposite the other.

We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.

Example 2: Evaluating Trigonometric Functions of Angles Not in Standard Position

Using the triangle shown in Figure 6, evaluate [latex]\sin \alpha \\[/latex], [latex]\cos \alpha \\[/latex], [latex]\tan \alpha \\[/latex], [latex]\sec \alpha\\[/latex], [latex]\csc \alpha[/latex], and [latex]\cot \alpha\\[/latex].

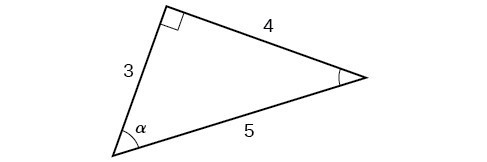
Figure 6

 

Try It 2

Using the triangle shown in Figure 7, evaluate [latex]\sin \text{ }t\\[/latex], [latex]\cos \text{ }t\\[/latex], [latex]\tan \text{ }t\\[/latex], [latex]\sec \text{ }t\\[/latex], [latex]\csc \text{ }t\\[/latex], and [latex]\cot \text{ }t\\[/latex].

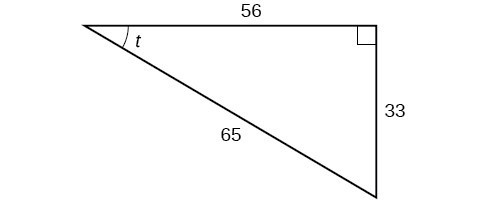
Figure 7

Solution

Finding Trigonometric Functions of Special Angles Using Side Lengths

We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of [latex]30^\circ[/latex], [latex]60^\circ[/latex], and [latex]45^\circ \\[/latex], however, remember that when dealing with right triangles, we are limited to angles between [latex]0^\circ \text{ and 90^\circ }\text{.}\\[/latex]

Suppose we have a [latex]30^\circ ,60^\circ ,90^\circ \\[/latex] triangle, which can also be described as a [latex]\frac{\pi }{6},\text{ } \frac{\pi }{3},\frac{\pi }{2}\\[/latex] triangle. The sides have lengths in the relation [latex]s,\sqrt{3}s,2s\\[/latex]. The sides of a [latex]45^\circ ,45^\circ ,90^\circ[/latex] triangle, which can also be described as a [latex]\frac{\pi }{4},\frac{\pi }{4},\frac{\pi }{2}\\[/latex] triangle, have lengths in the relation [latex]s,s,\sqrt{2}s\\[/latex]. These relations are shown in Figure 8.

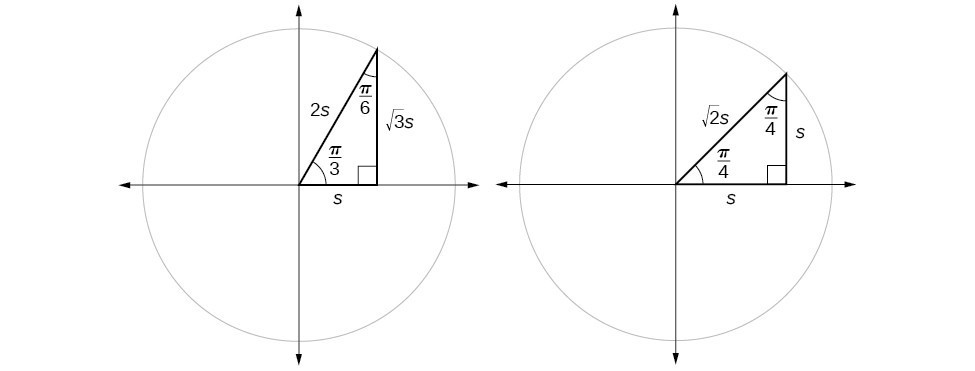
Figure 8. Side lengths of special triangles

We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.