Learning Outcomes
- Solve problems involving the roots and intercepts of a quadratic function.
- Solve problems involving a quadratic function’s minimum or maximum value.
In this section we will investigate quadratic functions further, including solving problems involving revenue, area, and projectile motion. Working with quadratic functions can be less complex than working with higher degree polynomial functions, so they provide a good opportunity for a detailed study of function behavior.
There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.

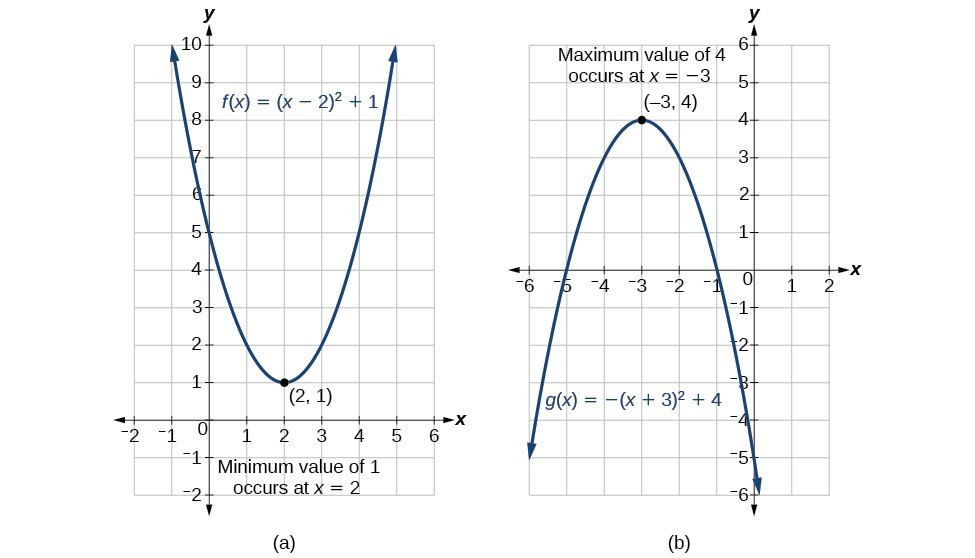
Figure 9
Example
A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.
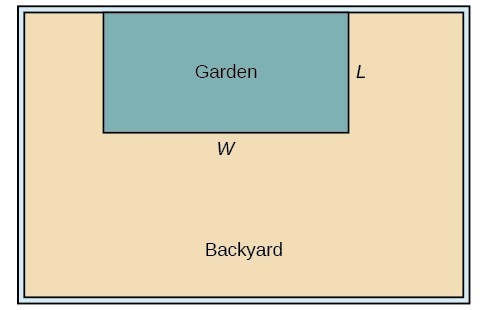
- Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length L.
- What dimensions should she make her garden to maximize the enclosed area?
SOLUTION
Let’s use a diagram above to record the given information. It is also helpful to introduce a temporary variable, W, to represent the width of the garden and the length of the fence section parallel to the backyard fence.
- We know we have only 80 feet of fence available, and [latex]L+W+L=80[/latex], or more simply, [latex]2L+W=80[/latex]. This allows us to represent the width, W, in terms of L.
[latex]W=80 - 2L[/latex]
Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so
[latex]\begin{cases}\text{ }A=LW=L\left(80 - 2L\right)\hfill \\ A\left(L\right)=80L - 2{L}^{2}\hfill \end{cases}[/latex]
This formula represents the area of the fence in terms of the variable length L. The function, written in general form, is
[latex]A\left(L\right)=-2{L}^{2}+80L[/latex].
- The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since a is the coefficient of the squared term, [latex]a=-2,b=80[/latex], and [latex]c=0[/latex].
To find the vertex:
[latex]\begin{cases}h=-\frac{80}{2\left(-2\right)}\hfill & \hfill & \hfill & \hfill & k=A\left(20\right)\hfill \\ \text{ }=20\hfill & \hfill & \text{and}\hfill & \hfill & \text{ }=80\left(20\right)-2{\left(20\right)}^{2}\hfill \\ \hfill & \hfill & \hfill & \hfill & \text{ }=800\hfill \end{cases}[/latex]
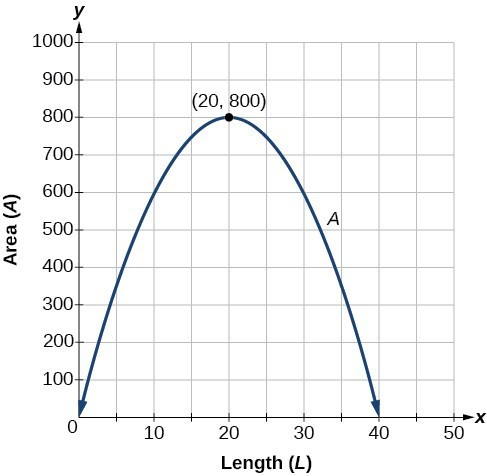
The maximum value of the function is an area of 800 square feet, which occurs when [latex]L=20[/latex] feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.
Analysis of the Solution
This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function in the figure below.
How To: Given an application involving revenue, use a quadratic equation to find the maximum.
- Write a quadratic equation for revenue.
- Find the vertex of the quadratic equation.
- Determine the y-value of the vertex.
Example
The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?
SOLUTION
Revenue is the amount of money a company brings in. In this case, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity. We can introduce variables, p for price per subscription and Q for quantity, giving us the equation [latex]\text{Revenue}=pQ[/latex].
Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently [latex]p=30[/latex] and [latex]Q=84,000[/latex]. We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, [latex]p=32[/latex] and [latex]Q=79,000[/latex]. From this we can find a linear equation relating the two quantities. The slope will be
[latex]\begin{cases}m=\frac{79,000 - 84,000}{32 - 30}\hfill \\ \text{ }=\frac{-5,000}{2}\hfill \\ \text{ }=-2,500\hfill \end{cases}[/latex]
This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the y-intercept.
[latex]\begin{cases}\text{ }Q=-2500p+b\hfill & \text{Substitute in the point }Q=84,000\text{ and }p=30\hfill \\ 84,000=-2500\left(30\right)+b\hfill & \text{Solve for }b\hfill \\ \text{ }b=159,000\hfill & \hfill \end{cases}[/latex]
This gives us the linear equation [latex]Q=-2,500p+159,000[/latex] relating cost and subscribers. We now return to our revenue equation.
[latex]\begin{cases}\text{Revenue}=pQ\hfill \\ \text{Revenue}=p\left(-2,500p+159,000\right)\hfill \\ \text{Revenue}=-2,500{p}^{2}+159,000p\hfill \end{cases}[/latex]
We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.
[latex]\begin{cases}h=-\frac{159,000}{2\left(-2,500\right)}\hfill \\ \text{ }=31.8\hfill \end{cases}[/latex]
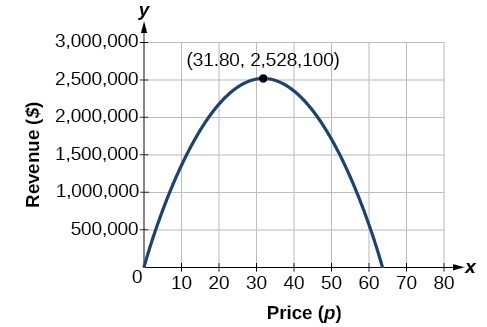
The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.
[latex]\begin{cases}\text{maximum revenue}=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right)\hfill \\ \text{ }=2,528,100\hfill \end{cases}[/latex]
Analysis of the Solution
This could also be solved by graphing the quadratic. We can see the maximum revenue on a graph of the quadratic function.
Example
A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+80t+40[/latex].
a. When does the ball reach the maximum height?
b. What is the maximum height of the ball?
c. When does the ball hit the ground?
Show Solution
a. The ball reaches the maximum height at the vertex of the parabola.
[latex]\begin{align}h&=-\dfrac{80}{2\left(-16\right)} \\[1mm]&=\dfrac{80}{32} \\[1mm] &=\dfrac{5}{2} \\[1mm] &=2.5 \end{align}[/latex]
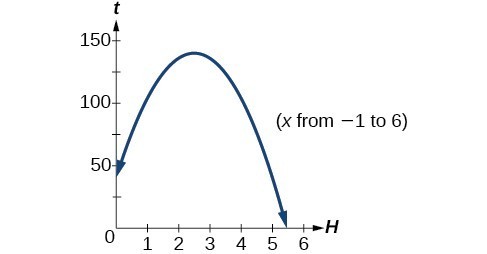
The ball reaches a maximum height after 2.5 seconds.
b. To find the maximum height, find the [latex]y[/latex] coordinate of the vertex of the parabola.
[latex]\begin{align}k&=H\left(2.5\right) \\[1mm] &=-16{\left(2.5\right)}^{2}+80\left(2.5\right)+40 \\[1mm] &=140\hfill \end{align}[/latex]
The ball reaches a maximum height of 140 feet.
c. To find when the ball hits the ground, we need to determine when the height is zero, [latex]H\left(t\right)=0[/latex].
We use the quadratic formula.
[latex]\begin{align} t&=\dfrac{-80\pm \sqrt{{80}^{2}-4\left(-16\right)\left(40\right)}}{2\left(-16\right)} \\[1mm] &=\dfrac{-80\pm \sqrt{8960}}{-32} \end{align}[/latex]
Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.
[latex]t=\dfrac{-80+\sqrt{8960}}{-32}\approx 5.458\hspace{3mm}[/latex] or [latex]\hspace{3mm}t=\dfrac{-80-\sqrt{8960}}{-32}\approx -0.458[/latex]
Since the domain starts at [latex]t=0[/latex] when the ball is thrown, the second answer is outside the reasonable domain of our model. The ball will hit the ground after about 5.46 seconds.
Try It
A rock is thrown upward from the top of a 112-foot high cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height above ocean can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+96t+112[/latex].
a. When does the rock reach the maximum height?
b. What is the maximum height of the rock?
c. When does the rock hit the ocean?
Show Solution
a. 3 seconds b. 256 feet c. 7 seconds
Applying
There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.
Example: Finding the Maximum Value of a Quadratic Function
A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.
- Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length [latex]L[/latex].
- What dimensions should she make her garden to maximize the enclosed area?
Show Solution
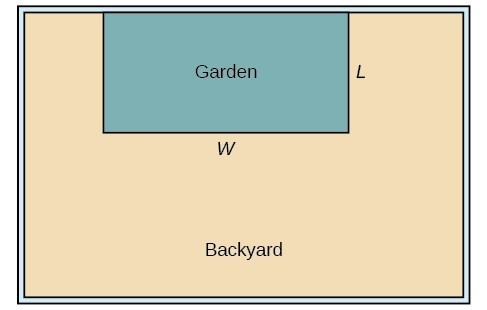
Let’s use a diagram such as the one above to record the given information. It is also helpful to introduce a temporary variable, [latex]W[/latex], to represent the width of the garden and the length of the fence section parallel to the backyard fence.
- We know we have only 80 feet of fence available, and [latex]L+W+L=80[/latex], or more simply, [latex]2L+W=80[/latex]. This allows us to represent the width, [latex]W[/latex], in terms of [latex]L[/latex].
[latex]W=80 - 2L[/latex]Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so [latex]A=LW=L\left(80 - 2L\right)=80L - 2{L}^{2}[/latex]. This formula represents the area of the fence in terms of the variable length [latex]L[/latex]. The function, written in general form, is[latex]A\left(L\right)=-2{L}^{2}+80L[/latex].
- The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since [latex]a[/latex] is the coefficient of the squared term, [latex]a=-2,b=80[/latex], and [latex]c=0[/latex].
To find the vertex:
[latex]h=-\dfrac{80}{2\left(-2\right)}=20[/latex]
and
[latex]\begin{align}k&=A\left(20\right) \\&=80\left(20\right)-2{\left(20\right)}^{2}\\&=800 \end{align}[/latex]
The maximum value of the function is an area of 800 square feet, which occurs when [latex]L=20[/latex] feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.
Analysis of the Solution
This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function below.
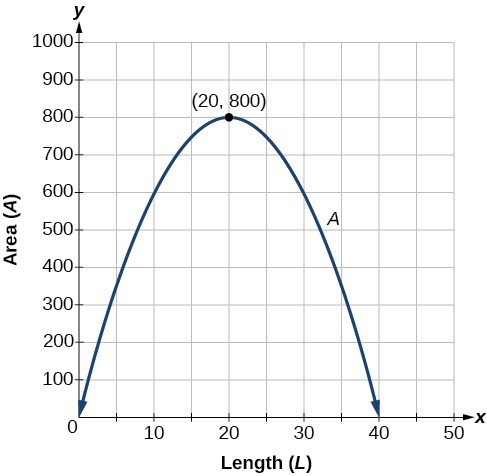
The problem we solved above is called a constrained optimization problem. We can optimize our desired outcome given a constraint, which in this case was a limited amount of fencing materials. Try it yourself in the next problem.
How To: Given an application involving revenue, use a quadratic equation to find the maximum.
- Write a quadratic equation for revenue.
- Find the vertex of the quadratic equation.
- Determine the [latex]y[/latex]-value of the vertex.
Example: Finding Maximum Revenue
The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?
Show Solution
Revenue is the amount of money a company brings in. In this case, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity. We can introduce variables, [latex]p[/latex] for price per subscription and [latex]Q[/latex] for quantity, giving us the equation [latex]\text{Revenue}=pQ[/latex].
Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently [latex]p=30[/latex] and [latex]Q=84,000[/latex]. We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, [latex]p=32[/latex] and [latex]Q=79,000[/latex]. From this we can find a linear equation relating the two quantities. The slope will be
[latex]\begin{align}m&=\dfrac{79,000 - 84,000}{32 - 30} \\ &=\dfrac{-5,000}{2} \\ &=-2,500 \end{align}[/latex]
This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the [latex]y[/latex]-intercept.
[latex]\begin{align}&Q=-2500p+b &&\text{Substitute in the point }Q=84,000\text{ and }p=30 \\ &84,000=-2500\left(30\right)+b &&\text{Solve for }b \\ &b=159,000 \end{align}[/latex]
This gives us the linear equation [latex]Q=-2,500p+159,000[/latex] relating cost and subscribers. We now return to our revenue equation.
[latex]\begin{align}&\text{Revenue}=pQ \\ &\text{Revenue}=p\left(-2,500p+159,000\right) \\ &\text{Revenue}=-2,500{p}^{2}+159,000p \end{align}[/latex]
We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.
[latex]\begin{align}h&=-\dfrac{159,000}{2\left(-2,500\right)} \\ &=31.8 \end{align}[/latex]
The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.
[latex]\begin{align}\text{maximum revenue}&=-2,500{\left(31.8\right)}^{2}+159,000\left(31.8\right) \\ &=\$2,528,100\hfill \end{align}[/latex]
Analysis of the Solution
This could also be solved by graphing the quadratic. We can see the maximum revenue on a graph of the quadratic function.
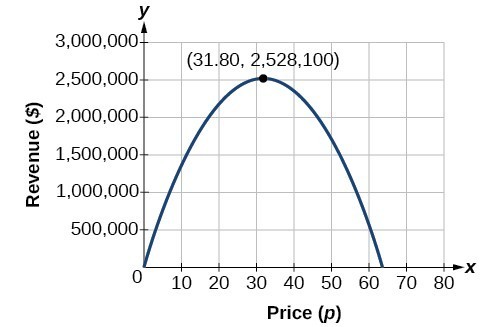
In the example above, we knew the number of subscribers to a newspaper and used that information to find the optimal price for each subscription. What if the price of subscriptions is affected by competition?
try it
Previously, we found a quadratic function that modeled revenue as a function of price.
[latex]\text{Revenue}-2,500{p}^{2}+159,000p[/latex]
We found that selling the paper at [latex]\$31.80[/latex] per subscription would maximize revenue. What if your closest competitor sells their paper for [latex]\$25.00[/latex] per subscription? What is the maximum revenue you can make you sell your paper for the same?
Show Solution
Evaluating the function for [latex]p=25[/latex] gives [latex]\$2,412,500[/latex].
Key Equations
The quadratic formula [latex]x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex]
The discriminant is defined as [latex]b^2-4ac[/latex]
Key Concepts
- The zeros, or [latex]x[/latex]-intercepts, are the points at which the parabola crosses the [latex]x[/latex]-axis. The [latex]y[/latex]-intercept is the point at which the parabola crosses the [latex]y[/latex]–axis.
- The vertex can be found from an equation representing a quadratic function.
- A quadratic function’s minimum or maximum value is given by the [latex]y[/latex]-value of the vertex.
- The minium or maximum value of a quadratic function can be used to determine the range of the function and to solve many kinds of real-world problems, including problems involving area and revenue.
- Some quadratic equations must be solved by using the quadratic formula.
- The vertex and the intercepts can be identified and interpreted to solve real-world problems.
- Some quadratic functions have complex roots.
Glossary
- discriminant
- the value under the radical in the quadratic formula, [latex]b^2-4ac[/latex], which tells whether the quadratic has real or complex roots
- vertex
- the point at which a parabola changes direction, corresponding to the minimum or maximum value of the quadratic function
- vertex form of a quadratic function
- another name for the standard form of a quadratic function
- zeros
- in a given function, the values of [latex]x[/latex] at which [latex]y=0[/latex], also called roots
Candela Citations
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 121416, 121401. Provided by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
CC licensed content, Shared previously
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 15809. Authored by: Sousa, James, mb Lippman, David. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 35145. Authored by: Jim Smart. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 2451. Authored by: Anderson, Tophe. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Question ID 15552. Authored by: David Lippman. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL








