Recall that the radian measure [latex]\theta[/latex] of an angle was defined as the ratio of the arc length [latex]s[/latex] of a circular arc to the radius [latex]r[/latex] of the circle, [latex]\theta =\frac{s}{r}[/latex]. From this relationship, we can find arc length along a circle, given an angle.
A General Note: Arc Length on a Circle
In a circle of radius r, the length of an arc [latex]s[/latex] subtended by an angle with measure [latex]\theta[/latex] in radians, shown in Figure 20, is
[latex]s=r\theta[/latex]
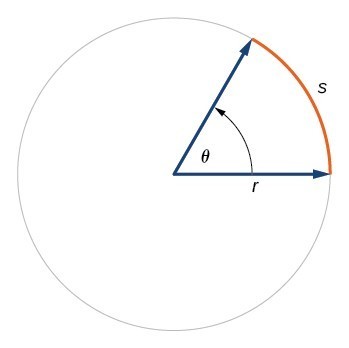
Figure 20
How To: Given a circle of radius [latex]r[/latex], calculate the length [latex]s[/latex] of the arc subtended by a given angle of measure [latex]\theta[/latex].
- If necessary, convert [latex]\theta[/latex] to radians.
- Multiply the radius [latex]r[/latex] by the radian measure of [latex]\theta :s=r\theta[/latex].
Example 8: Finding the Length of an Arc
Assume the orbit of Mercury around the sun is a perfect circle. Mercury is approximately 36 million miles from the sun.
- In one Earth day, Mercury completes 0.0114 of its total revolution. How many miles does it travel in one day?
- Use your answer from part (a) to determine the radian measure for Mercury’s movement in one Earth day.
Solution
- Let’s begin by finding the circumference of Mercury’s orbit.
[latex]\begin{array}{l}C=2\pi r\hfill \\ =2\pi \left(36\text{ million miles}\right)\hfill \\ \approx 226\text{ million miles}\hfill \end{array}[/latex]
Since Mercury completes 0.0114 of its total revolution in one Earth day, we can now find the distance traveled:
[latex]\left(0.0114\right)226\text{ million miles = 2}\text{.58 million miles}[/latex] - Now, we convert to radians:
[latex]\begin{array}{l}\text{radian}=\frac{\text{arclength}}{\text{radius}}\hfill \\ =\frac{2.\text{58 million miles}}{36\text{ million miles}}\hfill \\ =0.0717\hfill \end{array}[/latex]
Try It 8
Find the arc length along a circle of radius 10 units subtended by an angle of 215°.
Finding the Area of a Sector of a Circle
In addition to arc length, we can also use angles to find the area of a sector of a circle. A sector is a region of a circle bounded by two radii and the intercepted arc, like a slice of pizza or pie. Recall that the area of a circle with radius [latex]r[/latex] can be found using the formula [latex]A=\pi {r}^{2}[/latex]. If the two radii form an angle of [latex]\theta[/latex], measured in radians, then [latex]\frac{\theta }{2\pi }[/latex] is the ratio of the angle measure to the measure of a full rotation and is also, therefore, the ratio of the area of the sector to the area of the circle. Thus, the area of a sector is the fraction [latex]\frac{\theta }{2\pi }[/latex] multiplied by the entire area. (Always remember that this formula only applies if [latex]\theta[/latex] is in radians.)
A General Note: Area of a Sector
The area of a sector of a circle with radius [latex]r[/latex] subtended by an angle [latex]\theta[/latex], measured in radians, is
[latex]A=\frac{1}{2}\theta {r}^{2}[/latex]
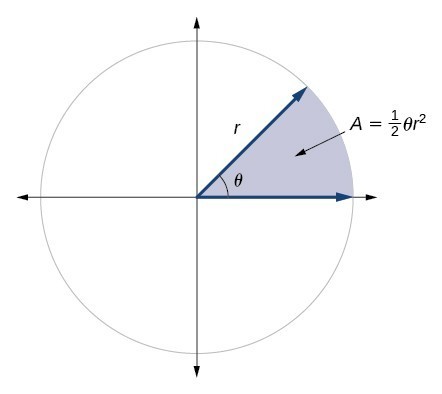
Figure 21. The area of the sector equals half the square of the radius times the central angle measured in radians.
How To: Given a circle of radius [latex]r[/latex], find the area of a sector defined by a given angle [latex]\theta[/latex].
- If necessary, convert [latex]\theta[/latex] to radians.
- Multiply half the radian measure of [latex]\theta[/latex] by the square of the radius [latex]r:\text{ } A=\frac{1}{2}\theta {r}^{2}[/latex].
Example 9: Finding the Area of a Sector
An automatic lawn sprinkler sprays a distance of 20 feet while rotating 30 degrees, as shown in Figure 22. What is the area of the sector of grass the sprinkler waters?
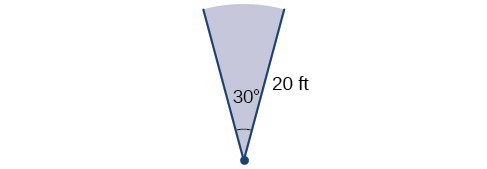
Figure 22. The sprinkler sprays 20 ft within an arc of 30°.
Solution
First, we need to convert the angle measure into radians. Because 30 degrees is one of our special angles, we already know the equivalent radian measure, but we can also convert:
The area of the sector is then
So the area is about [latex]104.72{\text{ ft}}^{2}[/latex].
Try It 9
In central pivot irrigation, a large irrigation pipe on wheels rotates around a center point. A farmer has a central pivot system with a radius of 400 meters. If water restrictions only allow her to water 150 thousand square meters a day, what angle should she set the system to cover? Write the answer in radian measure to two decimal places.
In the following video you will see how to calculate arc length and area of a sector of a circle.
Candela Citations
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution
- Arc Length and Area of a Sector. Authored by: Mathispower4u. Located at: https://youtu.be/zD4CsKIYEHo. License: All Rights Reserved. License Terms: Standard YouTube License