Dividing a circle into 360 parts is an arbitrary choice, although it creates the familiar degree measurement. We may choose other ways to divide a circle. To find another unit, think of the process of drawing a circle. Imagine that you stop before the circle is completed. The portion that you drew is referred to as an arc. An arc may be a portion of a full circle, a full circle, or more than a full circle, represented by more than one full rotation. The length of the arc around an entire circle is called the circumference of that circle.
The circumference of a circle is [latex]C=2\pi r[/latex]. If we divide both sides of this equation by [latex]r[/latex], we create the ratio of the circumference to the radius, which is always [latex]2\pi[/latex] regardless of the length of the radius. So the circumference of any circle is [latex]2\pi \approx 6.28[/latex] times the length of the radius. That means that if we took a string as long as the radius and used it to measure consecutive lengths around the circumference, there would be room for six full string-lengths and a little more than a quarter of a seventh, as shown in Figure 10.
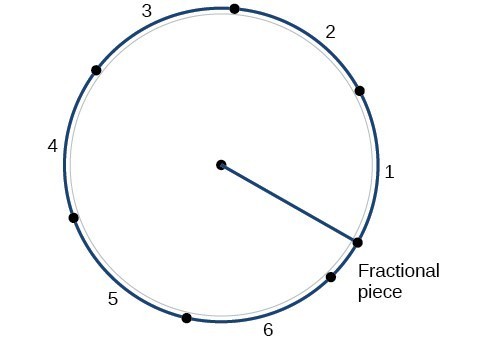
Figure 10
This brings us to our new angle measure. One radian is the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle. A central angle is an angle formed at the center of a circle by two radii. Because the total circumference equals [latex]2\pi[/latex] times the radius, a full circular rotation is [latex]2\pi[/latex] radians. So
Note that when an angle is described without a specific unit, it refers to radian measure. For example, an angle measure of 3 indicates 3 radians. In fact, radian measure is dimensionless, since it is the quotient of a length (circumference) divided by a length (radius) and the length units cancel out.
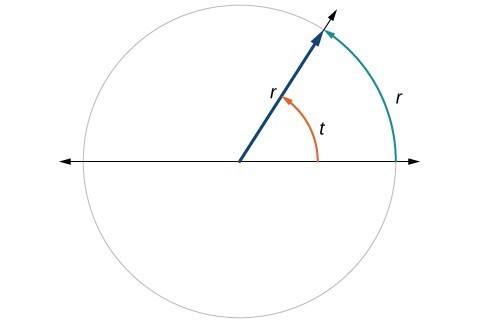
Figure 11. The angle t sweeps out a measure of one radian. Note that the length of the intercepted arc is the same as the length of the radius of the circle.
Relating Arc Lengths to Radius
An arc length [latex]s[/latex] is the length of the curve along the arc. Just as the full circumference of a circle always has a constant ratio to the radius, the arc length produced by any given angle also has a constant relation to the radius, regardless of the length of the radius.
This ratio, called the radian measure, is the same regardless of the radius of the circle—it depends only on the angle. This property allows us to define a measure of any angle as the ratio of the arc length [latex]s[/latex] to the radius [latex]r[/latex].
If [latex]s=r[/latex], then [latex]\theta =\frac{r}{r}=\text{ 1 radian}\text{.}[/latex]

Figure 12. (a) In an angle of 1 radian, the arc length [latex]s[/latex] equals the radius [latex]r[/latex]. (b) An angle of 2 radians has an arc length [latex]s=2r[/latex]. (c) A full revolution is [latex]2\pi[/latex] or about 6.28 radians.
To elaborate on this idea, consider two circles, one with radius 2 and the other with radius 3. Recall the circumference of a circle is [latex]C=2\pi r[/latex], where [latex]r[/latex] is the radius. The smaller circle then has circumference [latex]2\pi \left(2\right)=4\pi[/latex] and the larger has circumference [latex]2\pi \left(3\right)=6\pi[/latex]. Now we draw a 45° angle on the two circles, as in Figure 13.
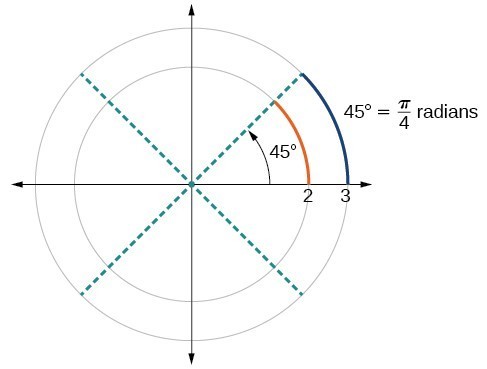
Figure 13. A 45° angle contains one-eighth of the circumference of a circle, regardless of the radius.
Notice what happens if we find the ratio of the arc length divided by the radius of the circle.
Since both ratios are [latex]\frac{1}{4}\pi[/latex], the angle measures of both circles are the same, even though the arc length and radius differ.
A General Note: Radians
One radian is the measure of the central angle of a circle such that the length of the arc between the initial side and the terminal side is equal to the radius of the circle. A full revolution (360°) equals [latex]2\pi[/latex] radians. A half revolution (180°) is equivalent to [latex]\pi[/latex] radians.
The radian measure of an angle is the ratio of the length of the arc subtended by the angle to the radius of the circle. In other words, if [latex]s[/latex] is the length of an arc of a circle, and [latex]r[/latex] is the radius of the circle, then the central angle containing that arc measures [latex]\frac{s}{r}[/latex] radians. In a circle of radius 1, the radian measure corresponds to the length of the arc.
Q & A
A measure of 1 radian looks to be about 60°. Is that correct?
Yes. It is approximately 57.3°. Because [latex]2\pi[/latex] radians equals 360°, [latex]1[/latex] radian equals [latex]\frac{360^\circ }{2\pi }\approx 57.3^\circ[/latex].
Using Radians
Because radian measure is the ratio of two lengths, it is a unitless measure. For example, in Figure 12, suppose the radius were 2 inches and the distance along the arc were also 2 inches. When we calculate the radian measure of the angle, the “inches” cancel, and we have a result without units. Therefore, it is not necessary to write the label “radians” after a radian measure, and if we see an angle that is not labeled with “degrees” or the degree symbol, we can assume that it is a radian measure.
Considering the most basic case, the unit circle (a circle with radius 1), we know that 1 rotation equals 360 degrees, 360°. We can also track one rotation around a circle by finding the circumference, [latex]C=2\pi r[/latex], and for the unit circle [latex]C=2\pi[/latex]. These two different ways to rotate around a circle give us a way to convert from degrees to radians.
Identifying Special Angles Measured in Radians
In addition to knowing the measurements in degrees and radians of a quarter revolution, a half revolution, and a full revolution, there are other frequently encountered angles in one revolution of a circle with which we should be familiar. It is common to encounter multiples of 30, 45, 60, and 90 degrees. These values are shown in Figure 14. Memorizing these angles will be very useful as we study the properties associated with angles.
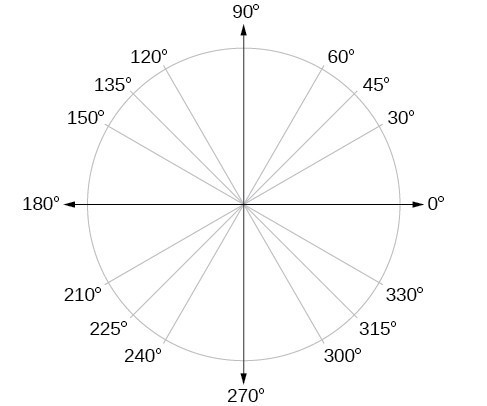
Figure 14. Commonly encountered angles measured in degrees
Now, we can list the corresponding radian values for the common measures of a circle corresponding to those listed in Figure 14, which are shown in Figure 15. Be sure you can verify each of these measures.
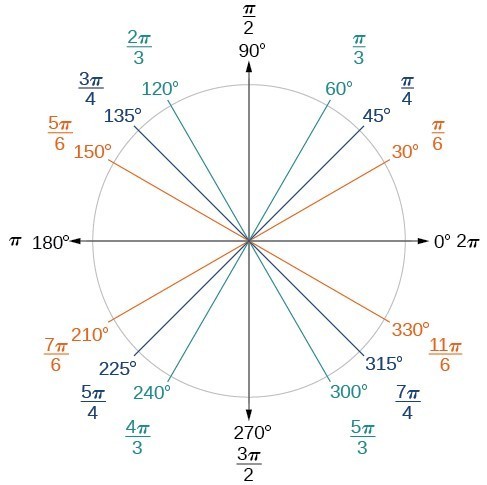
Figure 15. Commonly encountered angles measured in radians
Example 2: Finding a Radian Measure
Find the radian measure of one-third of a full rotation.
Solution
For any circle, the arc length along such a rotation would be one-third of the circumference. We know that
So,
The radian measure would be the arc length divided by the radius.
Converting between Radians and Degrees
Because degrees and radians both measure angles, we need to be able to convert between them. We can easily do so using a proportion.
This proportion shows that the measure of angle [latex]\theta[/latex] in degrees divided by 180 equals the measure of angle [latex]\theta[/latex] in radians divided by [latex]\pi .[/latex] Or, phrased another way, degrees is to 180 as radians is to [latex]\pi[/latex].
Converting between Radians and Degrees
To convert between degrees and radians, use the proportion
Example 3: Converting Radians to Degrees
Convert each radian measure to degrees.
a. [latex]\frac{\pi }{6}[/latex]
b. 3
Solution
Because we are given radians and we want degrees, we should set up a proportion and solve it.
a. We use the proportion, substituting the given information.
b. We use the proportion, substituting the given information.
[latex]\begin{array}{l}\begin{array}{l}\\ \frac{\theta }{180}=\frac{{\theta }^{R}}{\pi }\end{array}\hfill \\ \frac{\theta }{180}=\frac{3}{\pi }\hfill \\ \text{ }\theta =\frac{3\left(180\right)}{\pi }\hfill \\ \text{ }\theta \approx {172}^{\circ }\hfill \end{array}[/latex]
Example 4: Converting Degrees to Radians
Convert [latex]15[/latex] degrees to radians.
Solution
In this example, we start with degrees and want radians, so we again set up a proportion and solve it, but we substitute the given information into a different part of the proportion.
Analysis of the Solution
Another way to think about this problem is by remembering that [latex]{30}^{\circ }=\frac{\pi }{6}[/latex].
Because [latex]{15}^{\circ }=\frac{1}{2}\left({30}^{\circ }\right)[/latex], we can find that [latex]\frac{1}{2}\left(\frac{\pi }{6}\right)[/latex] is [latex]\frac{\pi }{12}[/latex].
Candela Citations
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution
- Radian Measure. Authored by: Mathispower4u. Located at: https://youtu.be/nAJqXtzwpXQ. License: All Rights Reserved. License Terms: Standard YouTube License